【問題】
【難易度】★★★☆☆(普通)
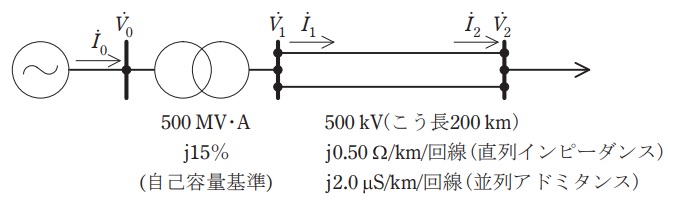
図に示す電源,変圧器,架空送電線から構成される三相が平衡した電力系統を対象として,四端子定数を用いてフェランチ効果の検討を行う。送電線は公称電圧\( \ 500 \ \mathrm {kV} \ \),こう長\( \ 200 \ \mathrm {km} \ \)の二回線送電線とし,その直列リアクタンスは\( \ 0.50 \ \mathrm {\Omega / km} \ \),並列サセプタンスは\( \ 2.0 \ \mathrm {\mu S / km} \ \)(ともに正相に対する一回線値)とする。また変圧器は容量\( \ 500 \ \mathrm {MV\cdot A} \ \)で,漏れリアクタンスは\( \ 15 \ \mathrm {%} \ \)(自己容量基準)とする。ここで,上記以外のインピーダンス等は全て無視する。
(1) 二回線送電線の\( \ \pi \ \)形等価回路を示し,回路中の直列インピーダンス,並列アドミタンスを単位法で記せ。ここで,基準容量は\( \ 1 \ 000 \ \mathrm {MV\cdot A} \ \)とし,基準電圧は線路の公称電圧とする。
小問(2)以降の計算は全て単位法で行う。
(2) 送電線の送電端の電圧\( \ {\dot V}_{1} \ \),電流\( \ {\dot I}_{1} \ \)をそれぞれ受電端の電圧\( \ {\dot V}_{2} \ \),電流\( \ {\dot I}_{2} \ \)で表す式を導出せよ。ここに\( \ {\dot I}_{1} \ \),\( \ {\dot I}_{2} \ \)は二回線合計の電流であり,その向きは図示のとおりとする。
(3) 電源の端子電圧\( \ {\dot V}_{0} \ \),電流\( \ {\dot I}_{0} \ \)をそれぞれ\( \ {\dot V}_{1} \ \),\( \ {\dot I}_{1} \ \)で表す式を導出せよ。ここに\( \ {\dot I}_{0} \ \)の向きは図に示すとおりとする。
(4) 送電線を無負荷\( \ \left( {\dot I}_{2}=0 \right) \ \)とするとき,送電線の受電端電圧の大きさ\( \ \left| {\dot V}_{2}\right| \ \)を求めよ。なお電源の端子電圧の大きさ\( \ \left| {\dot V}_{0}\right| \ \)は\( \ 1.05 \ \mathrm {p.u.} \ \)とする。
【ワンポイント解説】
四端子定数を用いた送電線の電圧計算に関する問題です。
解法自体は\( \ 1 \ \)種としてはそれほど難解ではなかったと思いますが,(1)で二回線送電線のインピーダンスやアドミタンスの取扱いを間違えると,その後も連鎖的に間違えてしまう落とし穴がありますので,十分に注意して取り組んで下さい。
1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \),基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \),基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時,インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと,
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}} (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.単位法における容量換算
「1.オーム法から単位法への変換」の通り,単位法のインピーダンスは基準容量に比例します。したがって,基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の単位法におけるインピーダンスは,
\[
\begin{eqnarray}
Z_{\mathrm {B}} \ \mathrm {[p.u.]}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}Z_{\mathrm {A}} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
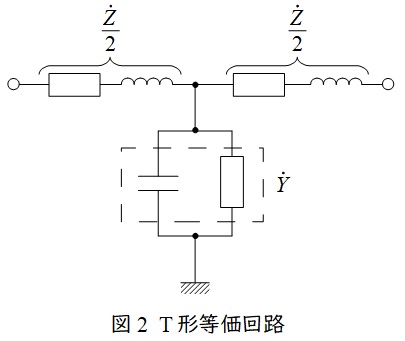
3.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路
送電線のこう長が大きくなると送電線のリアクタンスや静電容量が無視できなくなるので,\( \ \pi \ \)形等価回路や\( \ \mathrm {T} \ \)形等価回路を適用します。送電線のインピーダンスを\( \ \dot Z \ \),アドミタンスを\( \ \dot Y \ \)とすると,\( \ \pi \ \)形等価回路は図1,\( \ \mathrm {T} \ \)形等価回路は図2のようになります。
電験では送電線の抵抗分やサセプタンス分は無視し,送電線のインダクタンスを\( \ L \ \mathrm {[H]} \ \),静電容量を\( \ C \ \mathrm {[F]} \ \)として,
\[
\begin{eqnarray}
{\dot Z}&=&\mathrm {j}\omega L \\[ 5pt ]
{\dot Y}&=&\mathrm {j}\omega C \\[ 5pt ]
\end{eqnarray}
\]
として扱う問題がほとんどです。

【解答】
(1)二回線送電線の\( \ \pi \ \)形等価回路を示し,回路中の直列インピーダンス,並列アドミタンスを単位法で記す
二回線送電線の直列インピーダンス\( \ \dot Z \ \mathrm {[\Omega ]} \ \)及び並列アドミタンス\( \ \dot Y \ \mathrm {[\mu S]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}&=&\frac {\mathrm {j}0.50\times 200}{2} \\[ 5pt ]
&=&\mathrm {j}50 \ \mathrm {[\Omega ]} \\[ 5pt ]
{\dot Y}&=&\mathrm {j}2.0\times 200\times 2 \\[ 5pt ]
&=&\mathrm {j}800 \ \mathrm {[\mu S]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,それぞれ単位法で表すと,ワンポイント解説「1.オーム法から単位法への変換」の通り,
\[
\begin{eqnarray}
{\dot Z} \ \mathrm {[p.u.]}&=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}} \\[ 5pt ]
&=&\frac {1000\times 10^{6}\times \mathrm {j}50 }{\left( 500 \times 10^{3}\right) ^{2}} \\[ 5pt ]
&=&\mathrm {j}0.2 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot Y} \ \mathrm {[p.u.]}&=&\frac {V_{\mathrm {n}}^{2}Y \ \mathrm {[S]} \ }{P_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {\left( 500 \times 10^{3}\right) ^{2}\times \mathrm {j}800\times 10^{-6}}{1000\times 10^{6}} \\[ 5pt ]
&=&\mathrm {j}0.2 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,\( \ \pi \ \)形等価回路はワンポイント解説「3.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路」の通り図3のように描け,直列インピーダンス\( \ \dot Z=\mathrm {j}0.2 \ \mathrm {[p.u.]} \ \),並列アドミタンス\( \ \displaystyle \frac {\dot Y}{2}=\mathrm {j}0.1 \ \mathrm {[p.u.]} \ \)と求められる。
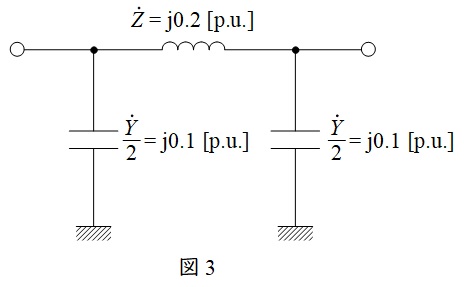
(2)\( \ {\dot V}_{1} \ \),\( \ {\dot I}_{1} \ \)をそれぞれ\( \ {\dot V}_{2} \ \),\( \ {\dot I}_{2} \ \)で表す式
図3より\( \ {\dot V}_{1} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{1}&=&{\dot V}_{2}+\dot Z\left( {\dot I}_{2}+\frac {\dot Y}{2}{\dot V}_{2}\right) \\[ 5pt ]
&=&{\dot V}_{2}+\mathrm {j}0.2\left( {\dot I}_{2}+\mathrm {j}0.1{\dot V}_{2}\right) \\[ 5pt ]
&=&{\dot V}_{2}+\mathrm {j}0.2{\dot I}_{2}-0.02{\dot V}_{2} \\[ 5pt ]
&=&0.98{\dot V}_{2}+\mathrm {j}0.2{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,同様に\( \ {\dot I}_{1} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {\dot Y}{2}{\dot V}_{1}+{\dot I}_{2}+\frac {\dot Y}{2}{\dot V}_{2} \\[ 5pt ]
&=&\mathrm {j}0.1\left( 0.98{\dot V}_{2}+\mathrm {j}0.2{\dot I}_{2}\right) +{\dot I}_{2}+\mathrm {j}0.1{\dot V}_{2} \\[ 5pt ]
&=&\mathrm {j}0.098{\dot V}_{2}-0.02{\dot I}_{2} +{\dot I}_{2}+\mathrm {j}0.1{\dot V}_{2} \\[ 5pt ]
&=&\mathrm {j}0.198{\dot V}_{2}+0.98{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ {\dot V}_{0} \ \),\( \ {\dot I}_{0} \ \)をそれぞれ\( \ {\dot V}_{1} \ \),\( \ {\dot I}_{1} \ \)で表す式
\( \ 1 \ 000 \ \mathrm {MV\cdot A} \ \)基準の変圧器のインピーダンス\( \ {\dot Z}_{\mathrm {T}} \ \mathrm {[p.u.]} \ \)は,ワンポイント解説「2.単位法における容量換算」の通り,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {T}}&=&\frac {1 \ 000}{500}\times \mathrm {j}0.15 \\[ 5pt ]
&=&\mathrm {j}0.3 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
{\dot V}_{0}&=&{\dot V}_{1}+{\dot Z}_{\mathrm {T}}{\dot I}_{1} \\[ 5pt ]
&=&{\dot V}_{1}+\mathrm {j}0.3{\dot I}_{1} \\[ 5pt ]
{\dot I}_{0}&=&{\dot I}_{1} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)無負荷\( \ \left( {\dot I}_{2}=0 \right) \ \)とするとき,送電線の受電端電圧の大きさ\( \ \left| {\dot V}_{2}\right| \ \)
(2)解答式及び(3)解答式を四端子定数で表すと,
\[
\begin{eqnarray}
\begin{pmatrix}
{\dot V}_{1} \\
{\dot I}_{1}
\end{pmatrix}&=&\begin{pmatrix}
0.98 & \mathrm {j}0.2 \\
\mathrm {j}0.198 & 0.98
\end{pmatrix}\begin{pmatrix}
{\dot V}_{2} \\
{\dot I}_{2}
\end{pmatrix} \\[ 5pt ]
\begin{pmatrix}
{\dot V}_{0} \\
{\dot I}_{0}
\end{pmatrix}&=&\begin{pmatrix}
1 & \mathrm {j}0.3 \\
0 & 1
\end{pmatrix}\begin{pmatrix}
{\dot V}_{1} \\
{\dot I}_{1}
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
であるから,この\( \ 2 \ \)式より,
\[
\begin{eqnarray}
\begin{pmatrix}
{\dot V}_{0} \\
{\dot I}_{0}
\end{pmatrix}&=&\begin{pmatrix}
1 & \mathrm {j}0.3 \\
0 & 1
\end{pmatrix}\begin{pmatrix}
0.98 & \mathrm {j}0.2 \\
\mathrm {j}0.198 & 0.98
\end{pmatrix}\begin{pmatrix}
{\dot V}_{2} \\
{\dot I}_{2}
\end{pmatrix} \\[ 5pt ]
&=&\begin{pmatrix}
0.98-0.0594 & \mathrm {j}0.2+\mathrm {j}0.294 \\
\mathrm {j}0.198 & 0.98
\end{pmatrix}\begin{pmatrix}
{\dot V}_{2} \\
{\dot I}_{2}
\end{pmatrix} \\[ 5pt ]
&=&\begin{pmatrix}
0.9206 & \mathrm {j}0.494 \\
\mathrm {j}0.198 & 0.98
\end{pmatrix}\begin{pmatrix}
{\dot V}_{2} \\
{\dot I}_{2}
\end{pmatrix} \\[ 5pt ]
\end{eqnarray}
\]
となる。題意より無負荷\( \ \left( {\dot I}_{2}=0 \right) \ \)であるから,
\[
\begin{eqnarray}
{\dot V}_{0}&=&0.9206{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,受電端電圧の大きさ\( \ \left| {\dot V}_{2}\right| \ \)は,
\[
\begin{eqnarray}
\left| {\dot V}_{2}\right| &=&\frac {\left| {\dot V}_{0}\right| }{0.9206} \\[ 5pt ]
&=&\frac {1.05}{0.9206} \\[ 5pt ]
&=&1.14 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
※問題文に四端子定数と記載があるので解答では四端子定数の行列を使用して解説していますが,実際の試験では下記の方法の通り(2)及び(3)の解答式に\( \ {\dot I}_{2}=0 \ \)を代入して,\( \ {\dot V}_{0}=0.9206{\dot V}_{2} \ \)を導き出しても良いかと思います。
(3)解答式に(2)解答式を代入すると,
\[
\begin{eqnarray}
{\dot V}_{0}&=&{\dot V}_{1}+\mathrm {j}0.3{\dot I}_{1} \\[ 5pt ]
&=&0.98{\dot V}_{2}+\mathrm {j}0.2{\dot I}_{2}+\mathrm {j}0.3\left( \mathrm {j}0.198{\dot V}_{2}+0.98{\dot I}_{2}\right) \\[ 5pt ]
&=&0.98{\dot V}_{2}+\mathrm {j}0.3\times \mathrm {j}0.198{\dot V}_{2} \\[ 5pt ]
&=&0.9206{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん