【問題】
【難易度】★★☆☆☆(やや易しい)
周波数\(50\mathrm {Hz}\)の電力系統において,電線1条当たりのインダクタンス\(1.6\mathrm {mH/km}\),静電容量\(0.01\mathrm {\mu F/km}\)の三相3線式送電線がある。この送電線のこう長が\(100\mathrm {km}\),回線数が2回線のとき,次の問に答えよ。なお,送電線は\(\mathrm {T}\)形等価回路で表されるものとし,抵抗及び漏れコンダクタンスは無視するものとする。
(1) 送電線の四端子定数\(\dot A\),\(\dot B\),\(\dot C\),\(\dot D\)をそれぞれ求めよ。
(2) 受電端開放の場合に,受電端の線間電圧\(\dot {V_{\mathrm {r}}}\)の大きさが\(275\mathrm {kV}\)のとき,送電端の線間電圧\(\dot {V_{\mathrm {s}}}\)の大きさ\(\mathrm {[kV]}\)を求めよ。
(3) 上記(2)の場合に,送電端から供給される無効電力\(\mathrm {[Mvar]}\)を求めよ。ただし,無効電力は遅れ側を正とする。
【ワンポイント解説】
若干厳しめですが,電験一種の計算問題としては平均よりやや易しめの問題なので★2つとしています。電験一種の二次試験には分布定数回路の問題が多数出題されかつ計算が複雑な問題もよく出題されます。計算間違いをしないように丁寧に解きたい問題です。
1.\(\mathrm {T}\)形等価回路
分布定数回路において,線路の抵抗とインダクタンスによるインピーダンスを\(\dot Z\),線路の静電容量と漏れコンダクタンスによるアドミタンスを\(\dot Y\)とすると,\(\mathrm {T}\)形等価回路は図1のように表すことができます。
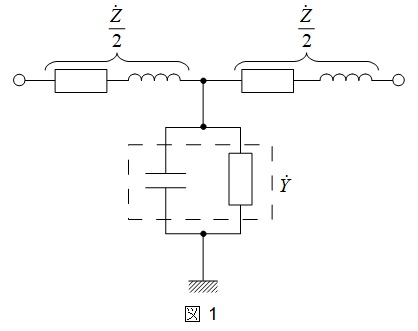
2.四端子定数
任意の図2のような回路がある時,送電端の相電圧\({\dot E}_{\mathrm {s}}\)と電流\({\dot I}_{\mathrm {s}}\),受電端の相電圧\({\dot E}_{\mathrm {r}}\)と電流\({\dot I}_{\mathrm {r}}\)の関係が以下の行列式で表されるものを四端子定数と言います。
\[
\begin{pmatrix} {\dot E}_{\mathrm {s}} \\ {\dot I}_{\mathrm {s}} \end{pmatrix} = \begin{pmatrix} \dot A & \dot B \\ \dot C & \dot D \end{pmatrix} \begin{pmatrix} {\dot E}_{\mathrm {r}} \\ {\dot I}_{\mathrm {r}} \end{pmatrix}
\]
ただし,
\[
\begin{eqnarray}
\dot A&=&\left. \frac {{\dot E}_{\mathrm {s}}}{{\dot E}_{\mathrm {r}}} \right| _{{\dot I}_{\mathrm {r}}=0}
\dot B&=&\left. \frac {{\dot E}_{\mathrm {s}}}{{\dot I}_{\mathrm {r}}} \right| _{{\dot E}_{\mathrm {r}}=0} \\[ 5pt ]
\dot C&=&\left. \frac {{\dot I}_{\mathrm {s}}}{{\dot E}_{\mathrm {r}}} \right| _{{\dot I}_{\mathrm {r}}=0}
\dot D&=&\left. \frac {{\dot I}_{\mathrm {s}}}{{\dot I}_{\mathrm {r}}} \right| _{{\dot E}_{\mathrm {r}}=0}
\end{eqnarray}
\]
となります。

【関連する「電気の神髄」記事】
【解答】
(1)送電線の四端子定数\(\dot A\),\(\dot B\),\(\dot C\),\(\dot D\)
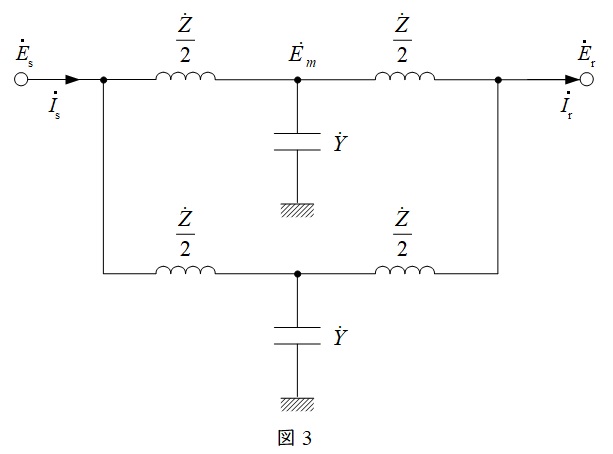
題意より送電線は2回線であるから,\(\mathrm {T}\)形等価回路を描くと図3のようになる。ただし,\({\dot E}_{\mathrm {s}}\),\({\dot I}_{\mathrm {s}}\),\({\dot E}_{\mathrm {r}}\),\({\dot I}_{\mathrm {r}}\)はそれぞれ,送電端の相電圧,送電端の電流,受電端の相電圧,受電端の電流である。
図3において\(\dot Z\)と\(\dot Y\)は,
\[
\begin{eqnarray}
\dot Z&=&\mathrm {j}2\pi f L \\[ 5pt ]
&=&\mathrm {j}2\pi \times 50\times 1.6\times 10^{-3}\times 100 \\[ 5pt ]
&≒&\mathrm {j}50.265 [ \Omega ] \\[ 5pt ]
\dot Y&=&\mathrm {j}2\pi f C \\[ 5pt ]
&=&\mathrm {j}2\pi \times 50\times 0.01\times 10^{-6}\times 100 \\[ 5pt ]
&≒&\mathrm {j}3.1416 \times 10^{-4} [ \mathrm {S} ]
\end{eqnarray}
\]
となる。ここで,中間点\({\dot E}_{\mathrm {m}}\)の電圧は,\(\displaystyle \frac {\dot Z}{2}\)に流れる電流が\(\displaystyle \frac {{\dot I}_{\mathrm {r}}}{2}\)であるから,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {m}}&=&{\dot E}_{\mathrm {r}}+\frac {\dot Z}{2}\cdot \frac {{\dot I}_{\mathrm {r}}}{2} \\[ 5pt ]
&=&{\dot E}_{\mathrm {r}}+\frac {\dot Z}{4}{\dot I}_{\mathrm {r}}
\end{eqnarray}
\]
となる。よって,コンデンサを流れる電流\({\dot I}_{\mathrm {y}}\)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {y}}&=&{\dot E}_{\mathrm {m}}\dot Y \\[ 5pt ]
&=&\left( {\dot E}_{\mathrm {r}}+\frac {\dot Z}{4}{\dot I}_{\mathrm {r}}\right) \dot Y \\[ 5pt ]
&=&\dot Y{\dot E}_{\mathrm {r}}+\frac {\dot Z\dot Y}{4}{\dot I}_{\mathrm {r}}
\end{eqnarray}
\]
となる。これより,送電端の電流\({\dot I}_{\mathrm {s}}\)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s}}&=&2\left( {\dot I}_{\mathrm {y}} + \frac {{\dot I}_{\mathrm {r}}}{2} \right) \\[ 5pt ]
&=&2\left( \dot Y{\dot E}_{\mathrm {r}}+\frac {\dot Z\dot Y}{4}{\dot I}_{\mathrm {r}} + \frac {{\dot I}_{\mathrm {r}}}{2} \right) \\[ 5pt ]
&=&2\dot Y{\dot E}_{\mathrm {r}}+\left( 1+\frac {\dot Z\dot Y}{2}\right) {\dot I}_{\mathrm {r}}
\end{eqnarray}
\]
となる。送電端の相電圧\({\dot E}_{\mathrm {s}}\)は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&{\dot E}_{\mathrm {m}} + \frac {\dot Z}{2}\cdot \frac {{\dot I}_{\mathrm {s}}}{2} \\[ 5pt ]
&=&{\dot E}_{\mathrm {r}}+\frac {\dot Z}{4}{\dot I}_{\mathrm {r}} + \frac {\dot Z}{2}\cdot \frac {1}{2}\left\{ 2\dot Y{\dot E}_{\mathrm {r}}+\left( 1+\frac {\dot Z\dot Y}{2}\right) {\dot I}_{\mathrm {r}}\right\} \\[ 5pt ]
&=&\left( 1+\frac {\dot Z\dot Y}{2}\right) {\dot E}_{\mathrm {r}}+\frac {\dot Z}{4}\left( 2+\frac {\dot Z\dot Y}{2}\right) {\dot I}_{\mathrm {r}}
\end{eqnarray}
\]
と求められる。以上より,\({\dot E}_{\mathrm {s}}\)と\({\dot I}_{\mathrm {s}}\)の式をワンポイント解説「2.四端子定数」の各パラメータとを比較すると,
\[
\begin{eqnarray}
\dot A&=&1+\frac {\dot Z\dot Y}{2} \\[ 5pt ]
\dot B&=&\frac {\dot Z}{4}\left( 2+\frac {\dot Z\dot Y}{2}\right) \\[ 5pt ]
\dot C&=&2\dot Y \\[ 5pt ]
\dot D&=&1+\frac {\dot Z\dot Y}{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\(\dot Z\)と\(\dot Y\)にそれぞれ値を代入すると,
\[
\begin{eqnarray}
\dot A&=&1+\frac {\mathrm {j}50.265 \times \mathrm {j}3.1416 \times 10^{-4}}{2} \\[ 5pt ]
&≒&0.99210 \\[ 5pt ]
\dot B&=&\frac {\mathrm {j}50.265}{4}\left( 2+\frac {\mathrm {j}50.265 \times \mathrm {j}3.1416 \times 10^{-4}}{2}\right) \\[ 5pt ]
&≒&\mathrm {j}25.033 [ \Omega ] \\[ 5pt ]
\dot C&=&2\times \mathrm {j}3.1416 \times 10^{-4} \\[ 5pt ]
&=&\mathrm {j}6.2832\times 10^{-4} [ \mathrm {S} ] \\[ 5pt ]
\dot D&=&1+\frac {\mathrm {j}50.265 \times \mathrm {j}3.1416 \times 10^{-4}}{2} \\[ 5pt ]
&≒&0.99210 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)受電端開放の場合の送電端の線間電圧\(\dot {V_{\mathrm {s}}}\)の大きさ
受電端開放である時,\({\dot I}_{\mathrm {r}}=0\)であるから,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}&=&\dot A {\dot E}_{\mathrm {r}} \\[ 5pt ]
\frac {{\dot V}_{\mathrm {s}}}{\sqrt {3}}&=&\dot A \frac {{\dot V}_{\mathrm {r}}}{\sqrt {3}} \\[ 5pt ]
{\dot V}_{\mathrm {s}}&=&\dot A {\dot V}_{\mathrm {r}}
\end{eqnarray}
\]
ここで,\(\dot A=0.99210\)及び\({\dot V}_{\mathrm {r}}=275\mathrm {kV}\)を代入すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s}}&=&\dot A {\dot V}_{\mathrm {r}} \\[ 5pt ]
&=&0.99210\times 275 \\[ 5pt ]
&≒&272.83 → 273 \ [\mathrm {kV}] \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)送電端から供給される無効電力\(\mathrm {[Mvar]}\)
送電端から供給される電力を\(P+\mathrm {j}Q\)とすると,題意より遅れ無効電力を正とするので,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&3 \dot A {\dot E}_{\mathrm {r}} \overline {\dot C {\dot E}_{\mathrm {r}}} \\[ 5pt ]
&=&3 \times 0.99210 \times \frac {275 \times 10^{3}}{\sqrt {3}} \times \left( -\mathrm {j}6.2832\times 10^{-4}\right) \times \frac {275 \times 10^{3}}{\sqrt {3}} \\[ 5pt ]
&≒&-\mathrm {j}47.141 \times 10^{6} → 47.1 \ [ \mathrm {Mvar}] (進み) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん