《電力・管理》〈送電〉[H28:問6] 電力系統における潮流計算に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

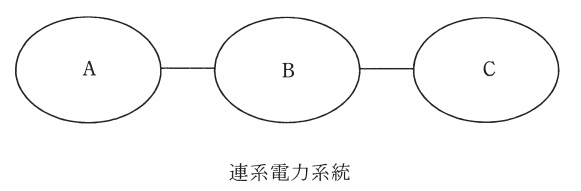
電力系統\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)及び\( \ \mathrm {C} \ \)が，図に示すように相互に連系されている。\( \ \mathrm {AB} \ \)間は非同期連系であり，\( \ \mathrm {BC} \ \)間は交流連系である。

\( \ \mathrm {A} \ \)で\( \ \mathrm {450 \ MW} \ \)の電源脱落が発生し，\( \ \mathrm {BC} \ \)間の連系潮流が，\( \ \mathrm {C} \ \)から\( \ \mathrm {B} \ \)の向きに\( \ \mathrm {214 \ MW} \ \)となった。ただし，電源脱落前における各電力系統の周波数はそれぞれの標準周波数，各連系潮流は\( \ \mathrm {0 \ MW} \ \)とし，電源脱落後の\( \ \mathrm {AB} \ \)間の連系潮流は，\( \ \mathrm {A} \ \)及び\( \ \mathrm {B} \ \)それぞれの周波数低下量の差に比例するものとする(比例定数を正とし，連系潮流は周波数低下量の小さい方から大きい方の向きを正とする)。なお，周波数低下量は，各電力系統の標準周波数を基準とする。

このとき，電源脱落後の以下の諸量を求めよ。諸元は次のとおりである(各記号の添字は，電力系統\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)又は\( \ \mathrm {C} \ \)を表す)。

・系統容量：\(S \ [\mathrm {MW}]\)
\[
S_{\mathrm {A}}=5 \ 000，S_{\mathrm {B}}=15 \ 000，S_{\mathrm {C}}=55 \ 000
\] ・パーセント系統定数：\(％K \ [\mathrm {％MW/Hz}]\)
\[
％K_{\mathrm {A}}=8，％K_{\mathrm {B}}=10，％K_{\mathrm {C}}=12
\]

(1)　\(\mathrm {C}\)の周波数低下量：\(\Delta F_{\mathrm {C}} \ [\mathrm {Hz}]\)

(2)　\(\mathrm {B}\)の周波数低下量：\(\Delta F_{\mathrm {B}} \ [\mathrm {Hz}]\)

(3)　\(\mathrm {AB}\)間の連系潮流：\(P_{\mathrm {AB}} \ [\mathrm {MW}]\)

(4)　\(\mathrm {A}\)の周波数低下量：\(\Delta F_{\mathrm {A}} \ [\mathrm {Hz}]\)

(5)　\(\mathrm {AB}\)間の連系潮流の比例定数：\(R_{\mathrm {AB}} \ [\mathrm {MW/Hz}]\)

ただし，(1)，(2)及び(4)は小数第3位を，(3)は小数第1位を，(5)は1の位を，それぞれ四捨五入して答えよ。

【ワンポイント解説】

電験一種としては比較的易しい問題と言えます。平成28年度の電力・管理の中では最も易しい問題なので，ほとんどの受験生が選択したと思われます。

【解答】

(1)\(\mathrm {C}\)の周波数低下量：\(\Delta F_{\mathrm {C}} \ [\mathrm {Hz}] \ \)
電力系統\(\mathrm {C}\)の系統定数\(K_{\mathrm {C}}\)は，
\[
\begin{eqnarray}
K_{\mathrm {C}}&=& ％K_{\mathrm {C}}S_{\mathrm {C}} \\[ 5pt ] &=&0.12 \times 55000 \\[ 5pt ] &=&6600 \ [\mathrm {MW/Hz}] \end{eqnarray}
\] となるので，周波数低下量\(\Delta F_{\mathrm {C}}\)は\(\mathrm {BC}\)間の連系潮流\(P_{\mathrm {BC}}\)が\( \ \mathrm {214 \ MW} \ \)であるから，
\[
\begin{eqnarray}
\Delta F_{\mathrm {C}}&=&\frac {P_{\mathrm {BC}}}{K_{\mathrm {C}}} \\[ 5pt ] &=&\frac {214}{6600} \\[ 5pt ] &≒&0.032424　→　0.03 \ [\mathrm {Hz}] \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)\(\mathrm {B}\)の周波数低下量：\(\Delta F_{\mathrm {B}}[\mathrm {Hz}]\)
\(\mathrm {BC}\)間は交流連系なので，周波数低下量は電力系統\(\mathrm {C}\)と等しい。よって，\(\Delta F_{\mathrm {B}}=0.03 \ [\mathrm {Hz}]\)

(3)\(\mathrm {AB}\)間の連系潮流：\(P_{\mathrm {AB}} \ [\mathrm {MW}]\)
電力系統\(\mathrm {B}\)の系統定数\(K_{\mathrm {B}}\)は，
\[
\begin{eqnarray}
K_{\mathrm {B}}&=& ％K_{\mathrm {B}}S_{\mathrm {B}} \\[ 5pt ] &=&0.1 \times 15000 \\[ 5pt ] &=&1500 \ [\mathrm {MW/Hz}] \end{eqnarray}
\] であるから，系統\(\mathrm {B}\)での電力低下量\(\Delta P_{\mathrm {B}}\)は，
\[
\begin{eqnarray}
\Delta P_{\mathrm {B}}&=& K_{\mathrm {B}}\Delta F_{\mathrm {B}} \\[ 5pt ] &=&1500 \times 0.032424 \\[ 5pt ] &=&48.636 \ [\mathrm {MW}] \end{eqnarray}
\] となる。よって，\(\mathrm {AB}\)間の連系潮流\(P_{\mathrm {AB}}\)は，
\[
\begin{eqnarray}
P_{\mathrm {AB}}&=& \Delta P_{\mathrm {B}}+P_{\mathrm {BC}} \\[ 5pt ] &=&48.636+214 \\[ 5pt ] &≒&262.64　→　263 \ [\mathrm {MW}] \end{eqnarray}
\] と求められる。

(4)\(\mathrm {A}\)の周波数低下量：\(\Delta F_{\mathrm {A}}[\mathrm {Hz}]\)
電力系統\(\mathrm {A}\)の系統定数\(K_{\mathrm {A}}\)は，
\[
\begin{eqnarray}
K_{\mathrm {A}}&=& ％K_{\mathrm {A}}S_{\mathrm {A}} \\[ 5pt ] &=&0.08 \times 5000 \\[ 5pt ] &=&400 \ [\mathrm {MW/Hz}] \end{eqnarray}
\] となる。また，系統\(\mathrm {A}\)での電力低下量\(\Delta P_{\mathrm {A}}\)は，電源脱落量\(\Delta G_{\mathrm {A}}=\mathrm {450MW}\)であるから，
\[
\begin{eqnarray}
\Delta P_{\mathrm {A}}&=&\Delta G_{\mathrm {A}}-P_{\mathrm {AB}} \\[ 5pt ] &=&450-262.64 \\[ 5pt ] &=&187.36 \ [\mathrm {MW}] \end{eqnarray}
\] であるから，\(\mathrm {A}\)の周波数低下量\(\Delta F_{\mathrm {A}}\)は，
\[
\begin{eqnarray}
\Delta F_{\mathrm {A}}&=&\frac {\Delta P_{\mathrm {A}}}{K_{\mathrm {A}}} \\[ 5pt ] &=&\frac {187.36}{400}
&=&0.4684　→　0.47 \ [\mathrm {Hz}] \end{eqnarray}
\] と求められる。

(5)\(\mathrm {AB}\)間の連系潮流の比例定数：\(R_{\mathrm {AB}}[\mathrm {MW/Hz}]\)
題意より，電源脱落後の\(\mathrm {AB}\)間の連系潮流は，\(\mathrm {A}\)及び\(\mathrm {B}\)それぞれの周波数低下量の差に比例するので，
\[
\begin{eqnarray}
P_{\mathrm {AB}}&=&R_{\mathrm {AB}}\left( \Delta F_{\mathrm {A}}-\Delta F_{\mathrm {B}}\right) \\[ 5pt ] R_{\mathrm {AB}}&=&\frac {P_{\mathrm {AB}}}{\Delta F_{\mathrm {A}}-\Delta F_{\mathrm {B}}} \\[ 5pt ] &=&\frac {262.64}{0.4684-0.032424} \\[ 5pt ] &≒&602　→　600 \ [\mathrm {MW/Hz}] \end{eqnarray}
\] と求められる。