《機械・制御》〈回転機〉[R04:問2]回生制動している三相誘導電動機に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

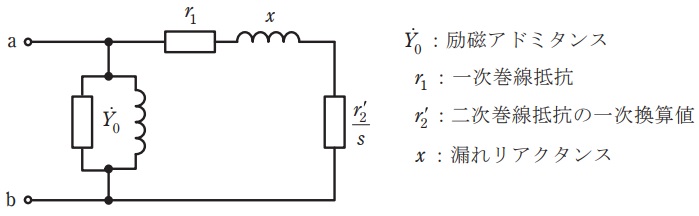
定格電圧\( \ 200 \ \mathrm {V} \ \)，定格周波数\( \ 50 \ \mathrm {Hz} \ \)，定格出力\( \ 15 \ \mathrm {kW} \ \)，\( \ 4 \ \)極の三相誘導電動機がある。図は滑り\( \ s \ \)で運転中の三相誘導電動機の星形一相分の\( \ \mathrm {L} \ \)形等価回路であり，各回路定数は次のとおりであった。
\[
\begin{eqnarray}
{\dot Y}_{0} &=&\frac {1}{0.625+\mathrm {j}15.5} \ \mathrm {S}，r_{1}=r_{2}^{\prime }=0.285 \ \Omega ，x=1.05 \ \Omega \\[ 5pt ] \end{eqnarray}
\] この電動機が\( \ 1590 \ \mathrm {{min}^{-1}} \ \)で回生制動している場合について，次の問に答えよ。ただし，機械損，漂遊負荷損は無視できるものとする。

(1)　同期速度\( \ N_{\mathrm {0}} \ \)及び滑り\( \ s \ \)を求めよ。

(2)　機械的な出力\( \ P_{\mathrm {m}} \ \)を求めよ。ただし，制動中の\( \ P_{\mathrm {m}} \ \)は負となる。

(3)　電動機トルク\( \ T \ \)を求めよ。

(4)　電源側に回生される電力\( \ P_{\mathrm {r}} \ \)を求めよ。

【ワンポイント解説】

回生制動している三相誘導電動機に関する問題です。
回生制動という状態が受験生を惑わせようという意図を感じますが，計算方法はすべて電動機運転の場合と変わりません。
したがって，滑り，出力，トルクが負となること等に注意して完答を狙うようにしましょう。

1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。また，同期角速度\( \ \omega _{\mathrm {s}} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] &=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ] &=&\frac {4\pi f}{p} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \)，回転数が\( \ N \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.誘導電動機の\( \ \mathrm {L} \ \)形等価回路
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \)は一次電流，\( \ {\dot I}_{2}^{\prime } \ \)は二次電流の一次換算値，\( \ {\dot I}_{0} \ \)は励磁電流，\( \ r_{1} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。

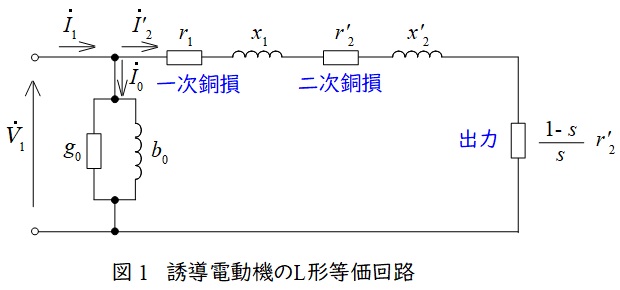
図1より，
\[
\begin{eqnarray}
I_{2}^{\prime } &=& \frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}} \\[ 5pt ] \end{eqnarray}
\] となるから，二次入力\( \ P_{2} \ \)は，
\[
\begin{eqnarray}
P_{2}&=&3\frac {r_{2}^{\prime}}{s}{I^{\prime}_{2}}^{2} \\[ 5pt ] &=&3\frac {r_{2}^{\prime}}{s}\cdot \left( {\frac {V_{1}}{\displaystyle \sqrt{\left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}}}\right) ^{2} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}}
\end{eqnarray}
\] となり，発生するトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T&=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {(1-s)P_{2}}{(1-s)\omega _{s}} \\[ 5pt ] &=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ] &=&\frac {3r_{2}^{\prime}}{\omega _{s}s}\cdot \frac {V_{1}^{2}}{\displaystyle \left( r_{1}+\frac {r_{2}^{\prime}}{s}\right) ^{2} +(x_{1}+x_{2}^{\prime}) ^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

4.滑り\( \ s \ \)と同期速度\( \ N_{\mathrm {s}} \ \)及び回転速度\( \ N \ \)の関係
誘導電動機は滑り\( \ s \ \)に応じて発電機もしくは電動機に状態が変化します。
①\( \ 0≦s≦1 \ \)のとき
　固定子磁界の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)の方が回転子の回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)より大きい状態であるため，誘導電動機の状態となります。したがって，回転子には正のトルクが発生することになります。

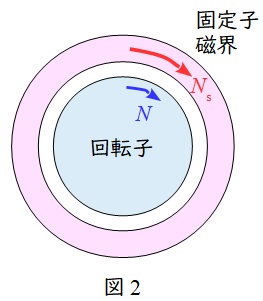
②\( \ s＜0 \ \)のとき
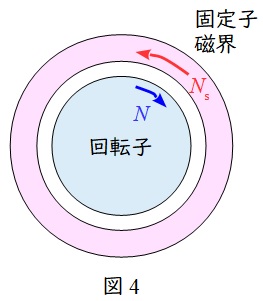
　回転子の回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)の方が固定子磁界の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)より大きい状態であるため，誘導発電機の状態となります。このとき，回転子には負のトルクが発生し，回生制動の状態となり電源側にエネルギーが回生されます。

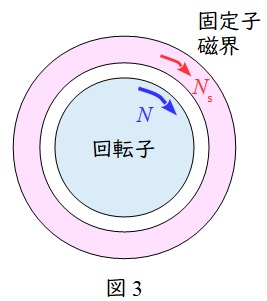
③\( \ s＞1 \ \)のとき
　固定子磁界の同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)と回転子の回転速度\( \ N \ \mathrm {[{min}^{-1}]} \ \)が逆方向の状態となるため，逆相制動の誘導電動機の状態となります。このとき，回転子には大きな負のトルクがかかり逆相制動と呼ばれる状態となります。固定子入力の\( \ 3 \ \)相のうち\( \ 2 \ \)相を入れ替えたとき，この状態になります。

【解答】

(1)同期速度\( \ N_{\mathrm {0}} \ \)及び滑り\( \ s \ \)
ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)」の通り，同期速度\( \ N_{\mathrm {0}} \ \mathrm {[{min}^{-1}]} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {0}} &=&\frac {120f}{p} \\[ 5pt ] &=&\frac {120\times 50}{4} \\[ 5pt ] &=&1 \ 500 \ \mathrm {[{min}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。また滑り\( \ s \ \)は，電動機が\( \ N=1 \ 590 \ \mathrm {[{min}^{-1}]} \ \)で運転しているので，ワンポイント解説「2.誘導機の滑り\( \ s \ \)」の通り，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {0}}-N}{N_{\mathrm {0}}} \\[ 5pt ] &=&\frac {1 \ 500-1 \ 590}{1 \ 500} \\[ 5pt ] &=&-0.06 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)出力\( \ P_{\mathrm {m}} \ \)
電動機の定格一次電圧を\( \ V_{1}=200 \ \mathrm {[V]} \ \)，負荷電流を\( \ I_{2}^{\prime } \ \mathrm {[A]} \ \)とすると，与えられている等価回路より，
\[
\begin{eqnarray}
I_{2}^{\prime } &=&\frac {\displaystyle \frac {V_{1}}{\sqrt {3}}}{\displaystyle \sqrt {\left( r_{1}+\frac {r_{2}^{\prime }}{s}\right) ^{2}+x^{2}}} \\[ 5pt ] &=&\frac {\displaystyle \frac {200}{\sqrt {3}}}{\displaystyle \sqrt {\left( 0.285+\frac {0.285}{-0.06}\right) ^{2}+1.05^{2}}} \\[ 5pt ] &≒&\frac {200}{\displaystyle \sqrt {3}\sqrt {21.039}} \\[ 5pt ] &≒&25.174 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，出力\( \ P_{\mathrm {m}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {m}} &=&3 \frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] &=&3 \times \frac {1-\left( -0.06\right)}{-0.06}\times 0.285 \times 25.174^{2} \\[ 5pt ] &≒&-9 \ 572.5 \ \mathrm {[W]}　→　-9.57 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)電動機トルク\( \ T \ \)
ワンポイント解説「3.誘導電動機の\( \ \mathrm {L} \ \)形等価回路」の通り，電動機トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，角速度\( \ \omega \ \mathrm {[rad / s]} \ \)とすると，
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {m}}}{\omega } \\[ 5pt ] &=&\frac {P_{\mathrm {m}}}{\displaystyle \frac {2\pi N}{60}} \\[ 5pt ] &=&\frac {-9 \ 572.5}{\displaystyle \frac {2\pi \times 1590 }{60} } \\[ 5pt ] &≒&-57.491　→　-57.5 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)電源側に回生される電力\( \ P_{\mathrm {r}} \ \)
電源側に回生される電力\( \ P_{\mathrm {r}} \ \mathrm {[kW]} \ \)は，機械的出力\( \ P_{\mathrm {m}} \ \mathrm {[kW]} \ \)から鉄損\( \ P_{\mathrm {i}} \ \mathrm {[W]} \ \)及び銅損\( \ P_{\mathrm {c}} \ \mathrm {[W]} \ \)を差し引いたものである。

鉄損\( \ P_{\mathrm {i}} \ \mathrm {[W]} \ \)及び銅損\( \ P_{\mathrm {c}} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {i}} &=&3\mathrm {Re} \left[ Y_{0}\right] \left( \frac {V_{1}}{\sqrt {3}} \right) ^{2} \\[ 5pt ] &=&3\times \mathrm {Re} \left[ \frac {1}{0.625+\mathrm {j}15.5}\right] \times \left( \frac {200}{\sqrt {3}} \right) ^{2} \\[ 5pt ] &=&3\times \mathrm {Re} \left[ \frac {1}{0.625+\mathrm {j}15.5}\times \frac {0.625-\mathrm {j}15.5}{0.625-\mathrm {j}15.5}\right] \times \frac {40 \ 000}{3} \\[ 5pt ] &=& \mathrm {Re} \left[ \frac {0.625-\mathrm {j}15.5}{0.625^{2}+15.5^{2}}\right] \times 40 \ 000 \\[ 5pt ] &=&\frac {0.625}{0.625^{2}+15.5^{2}} \times 40 \ 000 \\[ 5pt ] &≒&103.89 \ \mathrm {[W]} \\[ 5pt ] P_{\mathrm {c}} &=&3\left( r_{1}+r_{2}^{\prime }\right) {I_{2}^{\prime }}^{2} \\[ 5pt ] &=&3\times \left( 0.285+0.285\right) \times 25.174^{2} \\[ 5pt ] &≒&1 \ 083.7 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] となるので，電源に回生される電力\( \ P_{\mathrm {r}} \ \mathrm {[kW]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {r}} &=&-P_{\mathrm {m}}-P_{\mathrm {i}}-P_{\mathrm {c}} \\[ 5pt ] &=&9 \ 572.5-103.89-1 \ 083.7 \\[ 5pt ] &≒&8 \ 384.9 \ \mathrm {[W]}　→　8.38 \ \mathrm {[kW]} \\[ 5pt ] \end{eqnarray}
\] と求められる。