【問題】
【難易度】★★★☆☆(普通)
三相インバータの出力電圧に関して,次の問に答えよ。
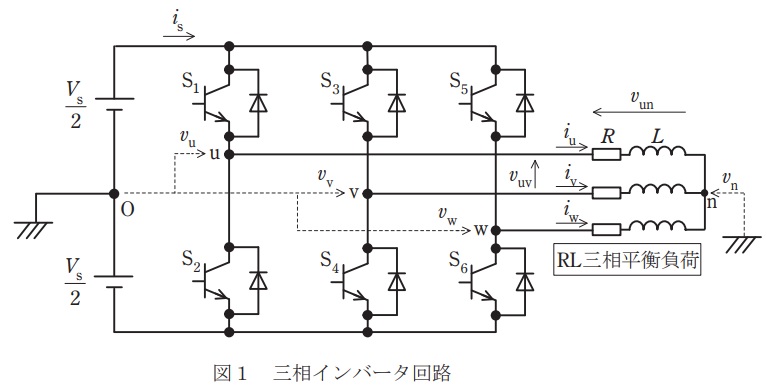
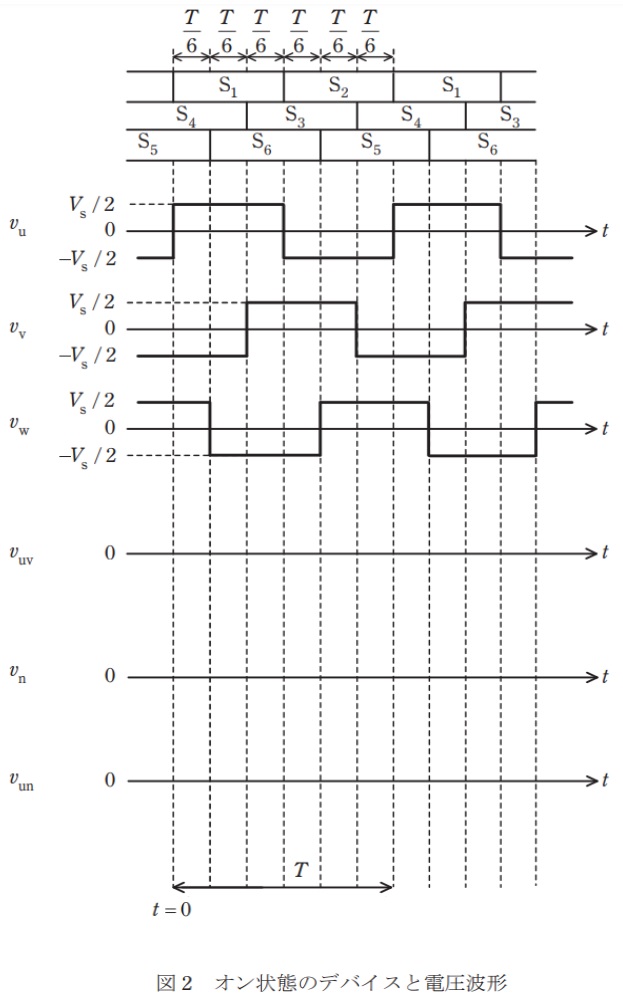
図1は,三相インバータの回路を示す。インバータの直流電源電圧を\( \ V_{\mathrm {s}} \ \)として,直流電源の中点\( \ \mathrm {O} \ \)を接地する。中点\( \ \mathrm {O} \ \)と点\( \ \mathrm {u} \ \),\( \ \mathrm {v} \ \),\( \ \mathrm {w} \ \)の間の電圧を\( \ v_{\mathrm {u}} \ \),\( \ v_{\mathrm {v}} \ \),\( \ v_{\mathrm {w}} \ \)とし,それらは\( \ \displaystyle \frac {V_{\mathrm {s}}}{2} \ \)または\( \ \displaystyle -\frac {V_{\mathrm {s}}}{2} \ \)となる。負荷は星形結線された\( \ \mathrm {RL} \ \)三相平衡負荷である。中点\( \ \mathrm {O} \ \)と負荷の中性点\( \ \mathrm {n} \ \)の間の電圧を\( \ v_{\mathrm {n}} \ \)とする。図2は,デバイス\( \ \mathrm {S_{1}} \ \)から\( \ \mathrm {S_{6}} \ \)のうちのオンのゲート信号が与えられているデバイスと,電圧\( \ v_{\mathrm {u}} \ \),\( \ v_{\mathrm {v}} \ \),\( \ v_{\mathrm {w}} \ \)の波形を示す。デバイス\( \ \mathrm {S_{1}} \ \)から\( \ \mathrm {S_{6}} \ \)のオンオフ切替の周期を\( \ T \ \)として,以下の問に答えよ。
(1) 線間電圧\( \ v_{\mathrm {uv}}=v_{\mathrm {u}}-v_{\mathrm {v}} \ \)を解答用紙の図に示せ。最大値と最小値を明示せよ。
(2) 負荷電流\( \ i_{\mathrm {u}} \ \),\( \ i_{\mathrm {v}} \ \),\( \ i_{\mathrm {w}} \ \)の和がゼロであることより,中点\( \ \mathrm {O} \ \)と負荷の中性点\( \ \mathrm {n} \ \)の間の電圧\( \ v_{\mathrm {n}} \ \)の式を電圧\( \ v_{\mathrm {u}} \ \),\( \ v_{\mathrm {v}} \ \),\( \ v_{\mathrm {w}} \ \)を用いて表せ。
(3) 小問(2)で求めた電圧\( \ v_{\mathrm {n}} \ \)を解答用紙の図に示せ。最大値と最小値を明示せよ。
(4) 負荷相電圧\( \ v_{\mathrm {un}}=v_{\mathrm {u}}-v_{\mathrm {n}} \ \)を解答用紙の図に示せ。最大値と最小値を明示せよ。
(5) 直流電源電流\( \ i_{\mathrm {s}} \ \)に含まれる変動成分の繰り返し周波数を求めよ。
【ワンポイント解説】
三相インバータの動作に関する問題です。
各スイッチ素子の動作を見ながら波形を描き,電圧値等を検討する三相インバータのメカニズムを理解するには非常にオススメの問題と言えます。
\( \ 1 \ \)種のパワーエレクトロニクスの問題としては比較的取り組みやすい問題であったかと思います。
1.三相インバータの動作
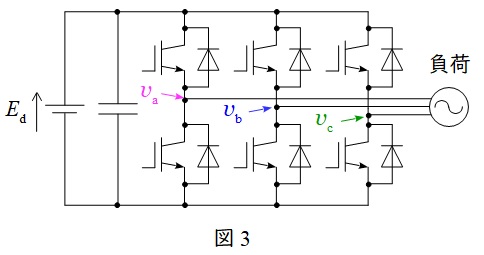
三相インバータは直流から交流を得る回路で,図3のような\( \ 6 \ \)つのスイッチで構成されています。
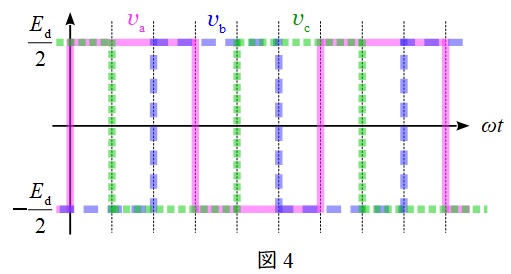
例えば,対応する正負のスイッチを\( \ \displaystyle \frac {2}{3}\pi \ \)ずつずらしてオンオフ制御すると,図4のように\( \ \displaystyle \frac {2}{3}\pi \ \)ずつずれた方形波が得られ,線間電圧を取れば図5のようなより正弦波に近い波形が得られます。
このとき,線間電圧の実効値\( \ V \ \)は,
\[
\begin{eqnarray}
V &=&\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }E_{\mathrm {d}}^{2}\mathrm {d}\theta } \\[ 5pt ]
&=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\int _{0}^{\frac {2}{3}\pi }1\mathrm {d}\theta } \\[ 5pt ]
&=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left[ \theta \right] _{0}^{\frac {2}{3}\pi }} \\[ 5pt ]
&=&E_{\mathrm {d}}\sqrt {\frac {1}{\pi }\left( \frac {2}{3}\pi -0 \right) } \\[ 5pt ]
&=&\sqrt {\frac {2}{3}}E_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
となります。

【解答】
(1)線間電圧\( \ v_{\mathrm {uv}} \ \)を示し,最大値と最小値を明示
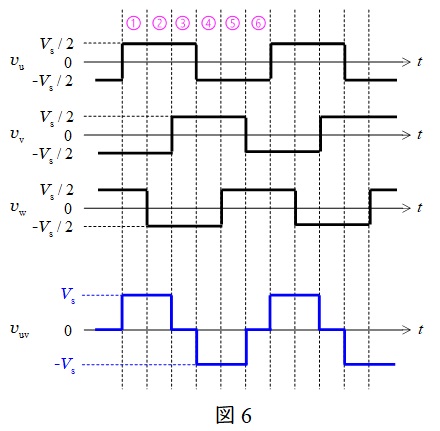
図6のように,スイッチのオンオフが変化するタイミング毎に①~⑥の領域に分けると,それぞれ\( \ v_{\mathrm {uv}}=v_{\mathrm {u}}-v_{\mathrm {v}} \ \)は,
①のとき,
\[
\begin{eqnarray}
v_{\mathrm {uv}} &=&\frac {V_{\mathrm {s}}}{2}-\left( -\frac {V_{\mathrm {s}}}{2}\right) \\[ 5pt ]
&=&V_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
②のとき,
\[
\begin{eqnarray}
v_{\mathrm {uv}} &=&\frac {V_{\mathrm {s}}}{2}-\left( -\frac {V_{\mathrm {s}}}{2}\right) \\[ 5pt ]
&=&V_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
③のとき,
\[
\begin{eqnarray}
v_{\mathrm {uv}} &=&\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2} \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
④のとき,
\[
\begin{eqnarray}
v_{\mathrm {uv}} &=&-\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2} \\[ 5pt ]
&=&-V_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
⑤のとき,
\[
\begin{eqnarray}
v_{\mathrm {uv}} &=&-\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2} \\[ 5pt ]
&=&-V_{\mathrm {s}} \\[ 5pt ]
\end{eqnarray}
\]
⑥のとき,
\[
\begin{eqnarray}
v_{\mathrm {uv}} &=&-\frac {V_{\mathrm {s}}}{2}-\left( -\frac {V_{\mathrm {s}}}{2}\right) \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,以降①~⑥を繰り返すので,\( \ v_{\mathrm {uv}} \ \)の波形は図6の通りとなり,最大値は\( \ V_{\mathrm {s}} \ \),最小値は\( \ -V_{\mathrm {s}} \ \)と求められる。
(2)中性点\( \ \mathrm {n} \ \)の間の電圧\( \ v_{\mathrm {n}} \ \)の式を電圧\( \ v_{\mathrm {u}} \ \),\( \ v_{\mathrm {v}} \ \),\( \ v_{\mathrm {w}} \ \)を用いて表す
図1の\( \ \mathrm {RL} \ \)三相平衡負荷について,
\[
\begin{eqnarray}
Ri_{\mathrm {u}}+L\frac {\mathrm {d}i_{\mathrm {u}}}{\mathrm {d}t} &=&v_{\mathrm {u}}-v_{\mathrm {n}} \\[ 5pt ]
Ri_{\mathrm {v}}+L\frac {\mathrm {d}i_{\mathrm {v}}}{\mathrm {d}t} &=&v_{\mathrm {v}}-v_{\mathrm {n}} \\[ 5pt ]
Ri_{\mathrm {w}}+L\frac {\mathrm {d}i_{\mathrm {w}}}{\mathrm {d}t} &=&v_{\mathrm {w}}-v_{\mathrm {n}} \\[ 5pt ]
\end{eqnarray}
\]
の回路方程式が立てられるので,左辺右辺ともに全て加えると,
\[
\begin{eqnarray}
R\left( i_{\mathrm {u}}+i_{\mathrm {v}}+i_{\mathrm {w}}\right) +L\frac {\mathrm {d}}{\mathrm {d}t}\left( i_{\mathrm {u}}+i_{\mathrm {v}}+i_{\mathrm {w}}\right) &=&v_{\mathrm {u}}+v_{\mathrm {v}}+v_{\mathrm {w}}-3v_{\mathrm {n}} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ i_{\mathrm {u}}+i_{\mathrm {v}}+i_{\mathrm {w}}=0 \ \)であることから,
\[
\begin{eqnarray}
0 &=&v_{\mathrm {u}}+v_{\mathrm {v}}+v_{\mathrm {w}}-3v_{\mathrm {n}} \\[ 5pt ]
3v_{\mathrm {n}} &=&v_{\mathrm {u}}+v_{\mathrm {v}}+v_{\mathrm {w}} \\[ 5pt ]
v_{\mathrm {n}} &=&\frac {v_{\mathrm {u}}+v_{\mathrm {v}}+v_{\mathrm {w}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)電圧\( \ v_{\mathrm {n}} \ \)を図に示し,最大値と最小値を明示
図7のように,スイッチのオンオフが変化するタイミング毎に①~⑥の領域に分けると,それぞれ\( \ \displaystyle v_{\mathrm {n}}=\frac {v_{\mathrm {u}}+v_{\mathrm {v}}+v_{\mathrm {w}}}{3} \ \)は,
①のとき,
\[
\begin{eqnarray}
v_{\mathrm {n}}&=&\frac {\displaystyle \frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2}+\frac {V_{\mathrm {s}}}{2}}{3} \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
②のとき,
\[
\begin{eqnarray}
v_{\mathrm {n}}&=&\frac {\displaystyle \frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2}}{3} \\[ 5pt ]
&=&-\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
③のとき,
\[
\begin{eqnarray}
v_{\mathrm {n}}&=&\frac {\displaystyle \frac {V_{\mathrm {s}}}{2}+\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2}}{3} \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
④のとき,
\[
\begin{eqnarray}
v_{\mathrm {n}}&=&\frac {\displaystyle -\frac {V_{\mathrm {s}}}{2}+\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2}}{3} \\[ 5pt ]
&=&-\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
⑤のとき,
\[
\begin{eqnarray}
v_{\mathrm {n}}&=&\frac {\displaystyle -\frac {V_{\mathrm {s}}}{2}+\frac {V_{\mathrm {s}}}{2}+\frac {V_{\mathrm {s}}}{2}}{3} \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
⑥のとき,
\[
\begin{eqnarray}
v_{\mathrm {n}}&=&\frac {\displaystyle -\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{2}+\frac {V_{\mathrm {s}}}{2}}{3} \\[ 5pt ]
&=&-\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
\end{eqnarray}
\]
となり,以降①~⑥を繰り返すので,\( \ v_{\mathrm {n}} \ \)の波形は図7の通りとなり,最大値は\( \ \displaystyle \frac {V_{\mathrm {s}}}{6} \ \),最小値は\( \ \displaystyle -\frac {V_{\mathrm {s}}}{6} \ \)と求められる。

(4)負荷相電圧\( \ v_{\mathrm {un}} \ \)を図に示し,最大値と最小値を明示
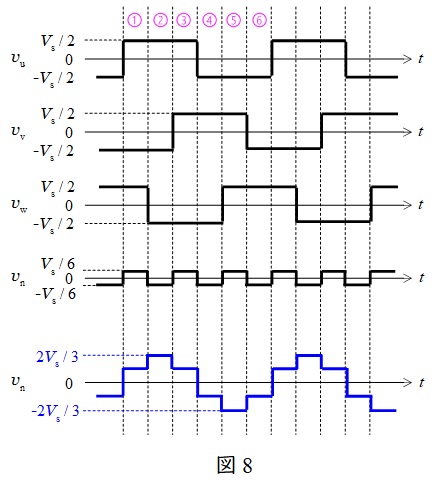
図8のように,スイッチのオンオフが変化するタイミング毎に①~⑥の領域に分けると,それぞれ\( \ \displaystyle v_{\mathrm {un}}=v_{\mathrm {u}}-v_{\mathrm {n}} \ \)は,
①のとき,
\[
\begin{eqnarray}
v_{\mathrm {un}}&=&\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
②のとき,
\[
\begin{eqnarray}
v_{\mathrm {un}}&=&\frac {V_{\mathrm {s}}}{2}-\left( -\frac {V_{\mathrm {s}}}{6}\right) \\[ 5pt ]
&=&\frac {2V_{\mathrm {s}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
③のとき,
\[
\begin{eqnarray}
v_{\mathrm {un}}&=&\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
④のとき,
\[
\begin{eqnarray}
v_{\mathrm {un}}&=&-\frac {V_{\mathrm {s}}}{2}-\left( -\frac {V_{\mathrm {s}}}{6}\right) \\[ 5pt ]
&=&-\frac {V_{\mathrm {s}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
⑤のとき,
\[
\begin{eqnarray}
v_{\mathrm {un}}&=&-\frac {V_{\mathrm {s}}}{2}-\frac {V_{\mathrm {s}}}{6} \\[ 5pt ]
&=&-\frac {2V_{\mathrm {s}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
⑥のとき,
\[
\begin{eqnarray}
v_{\mathrm {un}}&=&-\frac {V_{\mathrm {s}}}{2}-\left( -\frac {V_{\mathrm {s}}}{6}\right) \\[ 5pt ]
&=&-\frac {V_{\mathrm {s}}}{3} \\[ 5pt ]
\end{eqnarray}
\]
となり,以降①~⑥を繰り返すので,\( \ v_{\mathrm {un}} \ \)の波形は図8の通りとなり,最大値は\( \ \displaystyle \frac {2V_{\mathrm {s}}}{3} \ \),最小値は\( \ \displaystyle -\frac {2V_{\mathrm {s}}}{3} \ \)と求められる。
(5)直流電源電流\( \ i_{\mathrm {s}} \ \)に含まれる変動成分の繰り返し周波数
インバータは\( \ \displaystyle \frac {T}{6} \ \)毎にスイッチが切り替わり,変動成分はその都度生じる。三相平衡負荷の場合はどのタイミングにおいても同じ波形となるので,\( \ i_{\mathrm {s}} \ \)に含まれる変動成分の繰り返し周波数は\( \ \displaystyle \frac {6}{T} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん