【問題】
【難易度】★★☆☆☆(やや易しい)
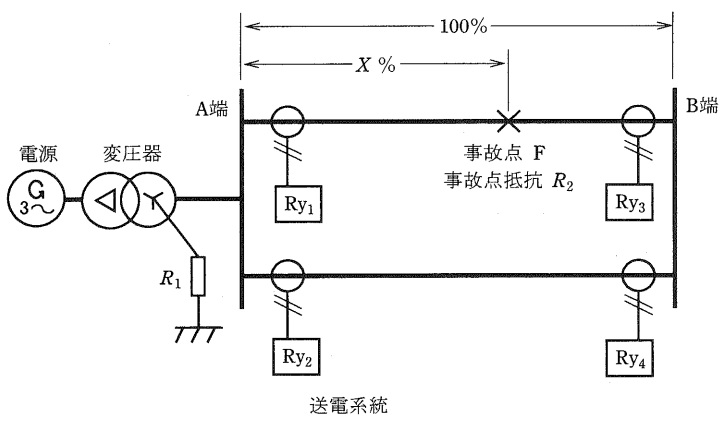
地絡方向リレーを設置した図のような送電系統を考える。送電線一回線に一線地絡事故が発生した場合のリレーの動作について,次の問に答えよ。
ただし,計算諸元は次のとおりとする。また,変圧器に接続されている中性点の接地抵抗は,送電線や変圧器のインピーダンスよりも非常に大きいものとし,送電線の静電容量は無視する。さらに,\( \ \mathrm {B} \ \)端は無負荷,無電源とする。
変電所送電端線間電圧 \( \ 77 \ 000 \ \mathrm {[V]} \ \)
\( \ \mathrm {A} \ \)端変圧器中性点の接地抵抗 \( \ R_{1} = 100 \ \mathrm {[\Omega ]} \ \)
地絡方向リレーの\( \ \mathrm {CT} \ \)比と整定値
\( \ \mathrm {A} \ \)端リレー\( \ \left( \mathrm {Ry_{1}},\mathrm {Ry_{2}}\right) \ \)\( \ \mathrm {CT} \ \)比:\( \ 1 \ 000 \ \mathrm {[A]}/5 \ \mathrm {[A]} \ \),整定値(電流):\( \ 0.30 \ \mathrm {[A]} \ \)
\( \ \mathrm {B} \ \)端リレー\( \ \left( \mathrm {Ry_{3}},\mathrm {Ry_{4}}\right) \ \)\( \ \mathrm {CT} \ \)比:\( \ 800 \ \mathrm {[A]}/5 \ \mathrm {[A]} \ \),整定値(電流):\( \ 0.40 \ \mathrm {[A]} \ \)
事故点までの距離と事故点抵抗
\( \ \mathrm {A} \ \)端~\( \ \mathrm {B} \ \)端の送電線の距離を\( \ 100 \ \mathrm {[%]} \ \)としたときの\( \ \mathrm {A} \ \)端~事故点\( \ \mathrm {F} \ \)までの距離:\( \ X \ \mathrm {[%]} \ \)
事故点\( \ \mathrm {F} \ \)の事故点抵抗:\( \ R_{2} \ \mathrm {[\Omega ]} \ \)
*事故点抵抗は純抵抗成分であるとする。
(1) \( \ X=60.0 \ \mathrm {[%]} \ \),\( \ R_{2}=0 \ \mathrm {[\Omega ]} \ \)であるとき,事故点\( \ \mathrm {F} \ \)に流れる地絡電流を求めよ。
(2) \( \ X=60.0 \ \mathrm {[%]} \ \),\( \ R_{2}=230 \ \mathrm {[\Omega ]} \ \)であるとき,\( \ \mathrm {Ry_{1}} \ \),\( \ \mathrm {Ry_{2}} \ \),\( \ \mathrm {Ry_{3}} \ \)に入力される電流の大きさをそれぞれ求めよ。
(3) \( \ R_{2}=230 \ \mathrm {[\Omega ]} \ \)であるとき,受電端(\( \ \mathrm {B} \ \)端)リレーが両回線ともに不動作,送電端(\( \ \mathrm {A} \ \)端)リレーが両回線ともに動作となり,受電端が停電する\( \ X \ \mathrm {[%]} \ \)の範囲を求めよ。
【ワンポイント解説】
一線地絡時のリレー動作に関する問題です。
一見問題文が長く難しそうに見えますが,基本的な公式以外はほとんど使わず,比較的取り組みやすい問題でした。
電力管理は機械制御に比べると幾分時間に余裕があるので,こういう問題を見逃さないように一通り問題に目を通すようにしましょう。
【解答】
(1)\( \ X=60.0 \ \mathrm {[%]} \ \),\( \ R_{2}=0 \ \mathrm {[\Omega ]} \ \)であるとき,事故点\( \ \mathrm {F} \ \)に流れる地絡電流
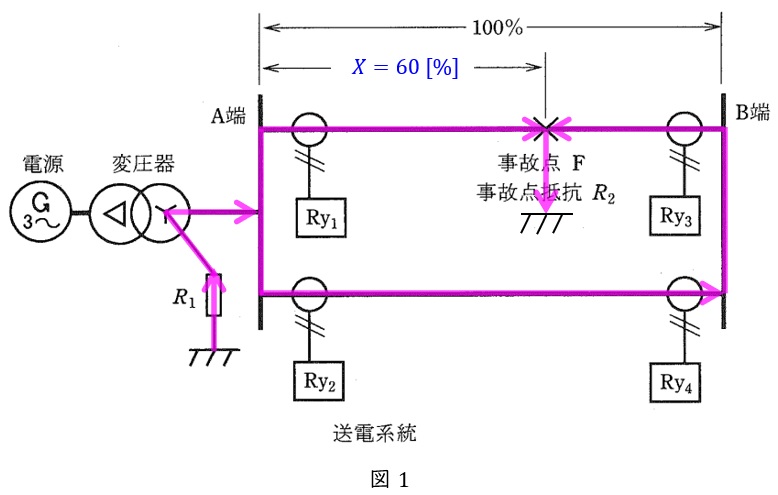
題意に沿って,事故時の電流の流れを記載すると,図1のようになる。
中性点の接地抵抗\( \ R_{1} = 100 \ \mathrm {[\Omega ]} \ \)は,送電線や変圧器のインピーダンスよりも非常に大きく\( \ R_{1} \ \)以外の抵抗は無視できるから,事故点\( \ \mathrm {F} \ \)に流れる地絡電流\( \ I_{\mathrm {f1}} \ \mathrm {[A]} \ \)は,送電線線間電圧\( \ V=77 \ 000 \ \mathrm {[V]} \ \)より,
\[
\begin{eqnarray}
I_{\mathrm {f1}}&=& \frac {\displaystyle \frac {V}{\sqrt{3}}}{R_{1}} \\[ 5pt ]
&=& \frac {\displaystyle \frac {77 \ 000}{\sqrt{3}}}{100} \\[ 5pt ]
&≒& 444.56 → 445 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ X=60.0 \ \mathrm {[%]} \ \),\( \ R_{2}=230 \ \mathrm {[\Omega ]} \ \)であるとき,\( \ \mathrm {Ry_{1}} \ \),\( \ \mathrm {Ry_{2}} \ \),\( \ \mathrm {Ry_{3}} \ \)に入力される電流
\( \ R_{1} = 100 \ \mathrm {[\Omega ]} \ \),\( \ R_{2}=230 \ \mathrm {[\Omega ]} \ \)より,事故点\( \ \mathrm {F} \ \)に流れる地絡電流\( \ I_{\mathrm {f2}} \ \mathrm {[A]} \ \)は,送電線線間電圧\( \ V=77 \ 000 \ \mathrm {[V]} \ \)より,
\[
\begin{eqnarray}
I_{\mathrm {f2}}&=& \frac {\displaystyle \frac {V}{\sqrt{3}}}{R_{1}+R_{2}} \\[ 5pt ]
&=& \frac {\displaystyle \frac {77 \ 000}{\sqrt{3}}}{100+230} \\[ 5pt ]
&≒& 134.72 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,事故電流は図1の通り,\( \ \mathrm {Ry_{1}} \ \)と\( \ \mathrm {Ry_{2}} \ \),\( \ \mathrm {Ry_{3}} \ \),\( \ \mathrm {Ry_{4}} \ \)に分流されるから,\( \ \mathrm {Ry_{1}} \ \),\( \ \mathrm {Ry_{2}} \ \),\( \ \mathrm {Ry_{3}} \ \)の一次側に流れる電流\( \ I_{\mathrm {Ry1}} \ \mathrm {[A]} \ \),\( \ I_{\mathrm {Ry2}} \ \mathrm {[A]} \ \),\( \ I_{\mathrm {Ry3}} \ \mathrm {[A]} \ \)は,分流の法則より,
\[
\begin{eqnarray}
I_{\mathrm {Ry1}}&=&\frac {200-X}{X+\left( 200-X\right) }I_{\mathrm {f2}} \\[ 5pt ]
&=&\frac {200-60}{60+\left( 200-60\right) }\times 134.72 \\[ 5pt ]
&=& 94.304 \ \mathrm {[A]} \\[ 5pt ]
I_{\mathrm {Ry2}}&=&\frac {X}{X+\left( 200-X\right) }I_{\mathrm {f2}} \\[ 5pt ]
&=&\frac {60}{60+\left( 200-60\right) }\times 134.72 \\[ 5pt ]
&=& 40.416 \ \mathrm {[A]} \\[ 5pt ]
I_{\mathrm {Ry3}}&=&I_{\mathrm {Ry2}} \\[ 5pt ]
&=& 40.416 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ \mathrm {Ry_{1}} \ \),\( \ \mathrm {Ry_{2}} \ \),\( \ \mathrm {Ry_{3}} \ \)に入力される電流\( \ i_{\mathrm {Ry1}} \ \mathrm {[A]} \ \),\( \ i_{\mathrm {Ry2}} \ \mathrm {[A]} \ \),\( \ i_{\mathrm {Ry3}} \ \mathrm {[A]} \ \)は,\( \ \mathrm {Ry_{1}} \ \)と\( \ \mathrm {Ry_{2}} \ \)の変流比が\( \ 1 \ 000 \ \mathrm {[A]}/5 \ \mathrm {[A]} \ \),\( \ \mathrm {Ry_{3}} \ \)の変流比が\( \ 800 \ \mathrm {[A]}/5 \ \mathrm {[A]} \ \)であるから,
\[
\begin{eqnarray}
i_{\mathrm {Ry1}}&=&\frac {5}{1 \ 000}I_{\mathrm {Ry1}} \\[ 5pt ]
&=&\frac {5}{1 \ 000}\times 94.304 \\[ 5pt ]
&=& 0.47152 → 0.472 \ \mathrm {[A]} \\[ 5pt ]
i_{\mathrm {Ry2}}&=&\frac {5}{1 \ 000}I_{\mathrm {Ry2}} \\[ 5pt ]
&=&\frac {5}{1 \ 000}\times 40.416 \\[ 5pt ]
&=& 0.20208 → 0.202 \ \mathrm {[A]} \\[ 5pt ]
i_{\mathrm {Ry3}}&=&\frac {5}{800}I_{\mathrm {Ry3}} \\[ 5pt ]
&=&\frac {5}{800}\times 40.416 \\[ 5pt ]
&=& 0.2526 → 0.253 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ R_{2}=230 \ \mathrm {[\Omega ]} \ \)であるとき,受電端(\( \ \mathrm {B} \ \)端)リレーが両回線ともに不動作,送電端(\( \ \mathrm {A} \ \)端)リレーが両回線ともに動作となり,受電端が停電する\( \ X \ \mathrm {[%]} \ \)
(2)より,\( \ i_{\mathrm {Ry1}}>i_{\mathrm {Ry2}} \ \)であり,\( \ \mathrm {Ry_{3}} \ \)と\( \ \mathrm {Ry_{4}} \ \)に流れる電流は等しいので,\( \ \mathrm {Ry_{2}} \ \)と\( \ \mathrm {Ry_{3}} \ \)について検討すれば良い。
\( \ \mathrm {Ry_{2}} \ \)の整定値\( \ i_{\mathrm {Ry2}}=0.30 \ \mathrm {[A]} \ \)及び\( \ \mathrm {Ry_{3}} \ \)の整定値\( \ i_{\mathrm {Ry3}}=0.40 \ \mathrm {[A]} \ \)の一次側換算値\( \ I_{\mathrm {Ry2}} \ \mathrm {[A]} \ \),\( \ I_{\mathrm {Ry3}} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {Ry2}}&=&\frac {1 \ 000}{5}i_{\mathrm {Ry2}} \\[ 5pt ]
&=&\frac {1 \ 000}{5}\times 0.30 \\[ 5pt ]
&=& 60 \ \mathrm {[A]} \\[ 5pt ]
I_{\mathrm {Ry3}}&=&\frac {800}{5}i_{\mathrm {Ry3}} \\[ 5pt ]
&=&\frac {800}{5}\times 0.40 \\[ 5pt ]
&=& 64 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。図1より\( \ I_{\mathrm {Ry2}} =I_{\mathrm {Ry3}} \ \)であるから,受電端(\( \ \mathrm {B} \ \)端)リレーが両回線ともに不動作,送電端(\( \ \mathrm {A} \ \)端)リレーが両回線ともに動作するためには\( \ 60≦I_{\mathrm {Ry2}}<64 \ \)であればよい。(2)と同様に\( \ I_{\mathrm {Ry2}} \ \mathrm {[A]} \ \)の大きさは,
\[
\begin{eqnarray}
I_{\mathrm {Ry2}}&=&\frac {X}{X+\left( 200-X\right) }I_{\mathrm {f2}} \\[ 5pt ]
&=&\frac {X}{200}\times 134.72 \\[ 5pt ]
&=&0.6736X \\[ 5pt ]
\end{eqnarray}
\]
なので,条件を満たす\( \ X \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
60&≦&I_{\mathrm {Ry2}}<64 \\[ 5pt ]
60&≦&0.6736X<64 \\[ 5pt ]
89.1&≦&X<95.0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん