【問題】
【難易度】★★★★☆(やや難しい)
送電線の二相短絡事故に関し,次の問に答えよ。
(1) 図1及び同期機の基本式を基にして,無負荷同期機の\( \ \mathrm {BC} \ \)相\( \ 2 \ \)線短絡事故時の正相,逆相,零相電圧\( \ {\dot V}_{1} \ \),\( \ {\dot V}_{2} \ \),\( \ {\dot V}_{0} \ \)及び正相,逆相,零相電流\( \ {\dot I}_{1} \ \),\( \ {\dot I}_{2} \ \),\( \ {\dot I}_{0} \ \)を発電機の正相誘導起電圧\( \ \dot E \ \),零相,正相,逆相インピーダンス\( \ {\dot Z}_{0} \ \),\( \ {\dot Z}_{1} \ \),\( \ {\dot Z}_{2} \ \)で表せ。

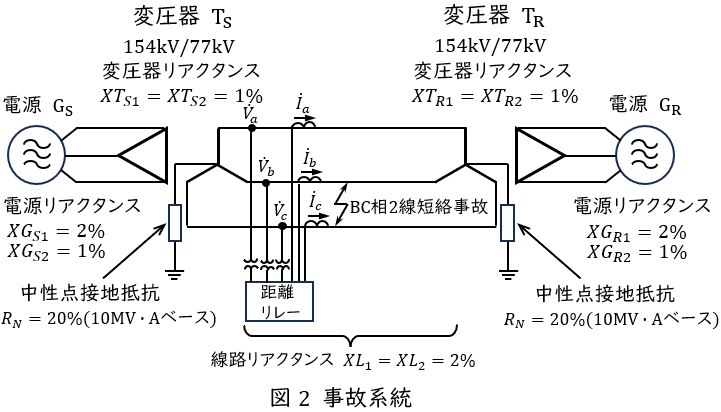
(2) 図2に示す系統において,\( \ 77 \ \mathrm {[kV]} \ \)送電線の中間地点(変圧器\( \ \mathrm {T}_{\mathrm {S}} \ \)及び\( \ \mathrm {T}_{\mathrm {R}} \ \)から等距離の地点)で\( \ \mathrm {BC} \ \)相\( \ 2 \ \)線短絡事故が発生した場合,変圧器\( \ \mathrm {T}_{\mathrm {S}} \ \)の\( \ 77 \ \mathrm {[kV]} \ \)側出口に設置された距離リレーに入力される各相の電流値及び電圧値(いずれも\( \ 77 \ \mathrm {[kV]} \ \)側換算値)を求めよ。ただし,位相については電源\( \ \mathrm {G}_{\mathrm {S}} \ \)の\( \ \mathrm {A} \ \)相内部誘起電圧を基準とする。また,電源\( \ \mathrm {G}_{\mathrm {S}} \ \),\( \ \mathrm {G}_{\mathrm {R}} \ \)の内部誘起電圧は\( \ 154 \ \mathrm {[kV]} \ \)とし,事故点のアーク抵抗及び発電機,変圧器,送電線の抵抗分は無視するものとする。
図中の%インピーダンスの値は,基準容量を\( \ 10 \ \mathrm {[MV\cdot A]} \ \)ベースとし,基準電圧は各系統電圧で表すものとする。また,添え字\( \ 1 \ \),\( \ 2 \ \)は正相及び逆相を表す。
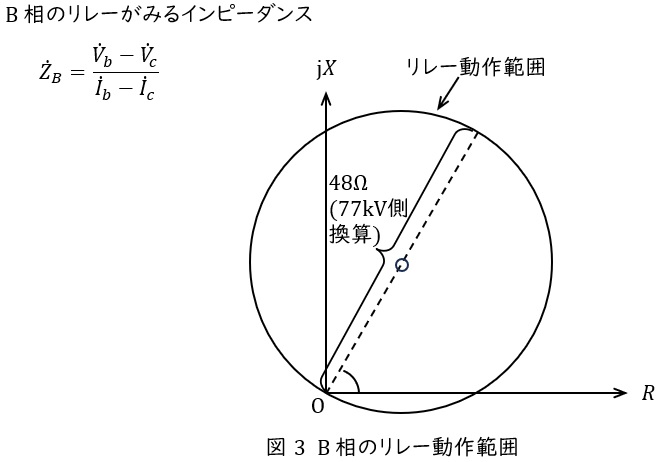
(3) (2)の事故時に\( \ \mathrm {B} \ \)相の距離リレーがみるインピーダンスを求め,リレーの動作範囲内にあるか判定せよ。ただし,距離リレーがみるインピーダンスは以下の通りとし,\( \ \mathrm {B} \ \)相のリレーの動作範囲は図3で示される円の内側で設定されているものとする。
【ワンポイント解説】
二相短絡事故時の電圧,電流を対称座標法を用いて求める問題です。
解法は比較的パターン化されていますが,計算量が多く,完答はかなり厳しい問題です。
最初は対称座標法の定義を覚えること,(1)の中身を理解することからスタートして下さい。
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータ\( \ a \ \)は,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
となります。上記より,
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ]
1+a+a^{2}&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
2.対称座標法
故障計算をする際に非常に便利な方法で,以下のように定義し対称座標変換されます。
零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-{\dot Z}_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-{\dot Z}_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-{\dot Z}_{2}{\dot I}_{2}
\end{eqnarray}
\]
【解答】
(1)\( \ \mathrm {BC} \ \)相\( \ 2 \ \)線短絡事故時の関係式
事故点での各相の電圧,電流をそれぞれ\( \ {\dot V}_{a} \ \),\( \ {\dot V}_{b} \ \),\( \ {\dot V}_{c} \ \),\( \ {\dot I}_{a} \ \),\( \ {\dot I}_{b} \ \),\( \ {\dot I}_{c} \ \)とおく。本問においては\( \ \mathrm {BC} \ \)相\( \ 2 \ \)線短絡が成立することから,\( \ {\dot V}_{b} = {\dot V}_{c} \ \),\( \ {\dot I}_{a}=0 \ \),\( \ {\dot I}_{b}=-{\dot I}_{c} \ \)が成立する。ここで,零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \),零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)として関係式を立てると,ワンポイント解説「2.対称座標法」の通り,
\[
\begin{eqnarray}
{\dot V}_{a} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} &・・・・・・・・・・・・ ①& \\[ 5pt ]
{\dot V}_{b} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2}={\dot V}_{c} &・・・・・・・・・・・・ ②& \\[ 5pt ]
{\dot V}_{c} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2}={\dot V}_{b} &・・・・・・・・・・・・ ③& \\[ 5pt ]
{\dot I}_{a} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2}=0 &・・・・・・・・・・・・ ④& \\[ 5pt ]
{\dot I}_{b} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}=-{\dot I}_{c} &・・・・・・・・・・・・ ⑤& \\[ 5pt ]
{\dot I}_{c} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}=-{\dot I}_{b} &・・・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
となる。②及び③より,
\[
\begin{eqnarray}
{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
a^{2}{\dot V}_{1} + a{\dot V}_{2} &=&a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\left( a^{2}-a\right) {\dot V}_{1}&=&\left( a^{2}-a\right) {\dot V}_{2} \\[ 5pt ]
{\dot V}_{1}&=&{\dot V}_{2} \ \ \ &・・・・・・・・ ⑦& \\[ 5pt ]
\end{eqnarray}
\]
となり,⑤及び⑥より,
\[
\begin{eqnarray}
{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} &=&-\left( {\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}\right) \\[ 5pt ]
2{\dot I}_{0}+ \left( a^{2}+a\right) {\dot I}_{1} + \left( a+a^{2}\right) {\dot I}_{2} &=&0 \\[ 5pt ]
2{\dot I}_{0}- {\dot I}_{1} -{\dot I}_{2} &=&0 \left( ∵a+a^{2}+1=0\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。さら④を上式に加えれば,
\[
\begin{eqnarray}
3{\dot I}_{0} &=&0 \\[ 5pt ]
{\dot I}_{0} &=&0 &・・・・・・・・・・・・・・・・・・・・・・・ ⑧& \\[ 5pt ]
\end{eqnarray}
\]
となり,これを④に代入すれば,
\[
\begin{eqnarray}
{\dot I}_{1} + {\dot I}_{2} &=&0 \\[ 5pt ]
{\dot I}_{1} &=&-{\dot I}_{2} \ \ &・・・・・・・・・・・・・・・・・・ ⑨& \\[ 5pt ]
\end{eqnarray}
\]
となる。⑦~⑨を発電機の基本式に適用すると,
\[
\begin{eqnarray}
{\dot V}_{0} &=&-{\dot Z}_{0}{\dot I}_{0} \\[ 5pt ]
&=&-{\dot Z}_{0}\times 0 \\[ 5pt ]
&=& 0 \ \ &・・・・・・・・・・・・ ⑩& \\[ 5pt ]
\dot E-{\dot Z}_{1}{\dot I}_{1} &=&-{\dot Z}_{2}{\dot I}_{2} \\[ 5pt ]
&=&{\dot Z}_{2}{\dot I}_{1} \\[ 5pt ]
\left( {\dot Z}_{1}+{\dot Z}_{2}\right) {\dot I}_{1} &=&\dot E \\[ 5pt ]
{\dot I}_{1} &=&\frac {\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} &・・・・・・・・・・・・ ⑪& \\[ 5pt ]
{\dot I}_{2} &=&-\frac {\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} &・・・・・・・・・・・・ ⑫& \\[ 5pt ]
\end{eqnarray}
\]
となり,⑪及び⑫を発電機の基本式に適用すれば,
\[
\begin{eqnarray}
{\dot V}_{1}={\dot V}_{2} &=&-{\dot Z}_{2}{\dot I}_{2} \\[ 5pt ]
&=&-{\dot Z}_{2}\left( -\frac {\dot E}{{\dot Z}_{1}+{\dot Z}_{2}}\right) \\[ 5pt ]
&=&\frac {{\dot Z}_{2}\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} \ \ &・・・・・・・・・・ ⑬& \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,⑧,⑩,⑪,⑫,⑬が求める関係式となる。
(2)\( \ \mathrm {BC} \ \)相\( \ 2 \ \)線短絡事故時,距離リレーに入力される各相の電流値及び電圧値
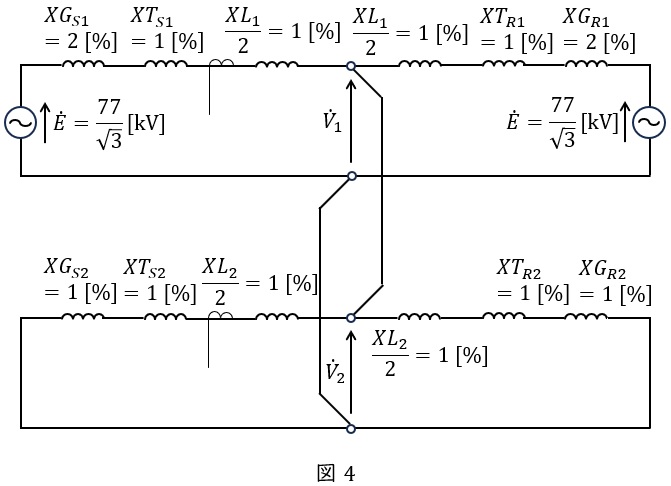
(1)より,\( \ \mathrm {BC} \ \)相\( \ 2 \ \)線短絡事故時の対称分等価回路は図4のようになる。
故障点からみた正相インピーダンス\( \ {\dot Z}_{1} \ \mathrm {[p.u.]} \ \)及び逆相インピーダンス\( \ {\dot Z}_{2} \ \mathrm {[p.u.]} \ \)は,図4の回路が左右対称であることから,
\[
\begin{eqnarray}
{\dot Z}_{1} &=&\frac {\displaystyle \mathrm {j}XG_{S1}+\mathrm {j}XT_{S1}+\frac {\mathrm {j}XL_{S1}}{2}}{2} \\[ 5pt ]
&=&\frac {\mathrm {j}0.02+\mathrm {j}0.01+\mathrm {j}0.01}{2} \\[ 5pt ]
&=&\mathrm {j}0.02 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot Z}_{2} &=&\frac {\displaystyle \mathrm {j}XG_{S2}+\mathrm {j}XT_{S2}+\frac {\mathrm {j}XL_{S2}}{2}}{2} \\[ 5pt ]
&=&\frac {\mathrm {j}0.01+\mathrm {j}0.01+\mathrm {j}0.01}{2} \\[ 5pt ]
&=&\mathrm {j}0.015 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。図1より,\( \ 2 \ \)線短絡事故時の短絡電流は\( \ {\dot I}_{b} \ \)であり,(1)より,
\[
\begin{eqnarray}
{\dot I}_{b} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
&=&0+ a^{2}{\dot I}_{1} – a{\dot I}_{1} \\[ 5pt ]
&=&\left( a^{2}-a\right){\dot I}_{1} \\[ 5pt ]
&=&\left\{ -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}-\left(-\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2}\right) \right\} \frac {\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} \left( ∵⑪\right) \\[ 5pt ]
&=&\frac {-\mathrm {j}\sqrt {3}\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} \\[ 5pt ]
&=&\frac {-\mathrm {j}\sqrt {3}\times 1}{\mathrm {j}0.02+\mathrm {j}0.015} \\[ 5pt ]
&=&-49.487 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,基準電流\( \ I_{n} \ \mathrm {[A]} \ \)は,
\[
\begin{eqnarray}
I_{n} &=&\frac {P_{n}}{\sqrt {3}V_{n}} \\[ 5pt ]
&=&\frac {10\times 10^{6}}{\sqrt {3}\times 77\times 10^{3}} \\[ 5pt ]
&≒&74.981 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
なので,短絡電流は,
\[
\begin{eqnarray}
{\dot I}_{b} &=&-49.487\times 74.981 \\[ 5pt ]
&≒&-3 \ 710.6 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。距離リレーに入力される電流値は,変圧器\( \ \mathrm {T}_{\mathrm {S}} \ \)側の電流,すなわち半分であるので,その各相の電流値\( \ {\dot I}_{Rb} \ \)及び\( \ {\dot I}_{Rc} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{Rb} &=&\frac {{\dot I}_{b}}{2} \\[ 5pt ]
&=&\frac {-3 \ 710.6}{2} \\[ 5pt ]
&=&-1 \ 855.3 → -1 \ 860 \ \mathrm {[A]} \\[ 5pt ]
{\dot I}_{Rc} &=&\frac {{\dot I}_{c}}{2} \\[ 5pt ]
&=&-\frac {{\dot I}_{b}}{2} \\[ 5pt ]
&=&-\frac {-3 \ 710.6}{2} \\[ 5pt ]
&=&1 \ 855.3 → 1 \ 860 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,事故発生時の事故点電圧\( \ {\dot V}_{b} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{b}={\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
&=&0+ a^{2}{\dot V}_{1} + a{\dot V}_{1} \left( ∵⑩,⑬\right) \\[ 5pt ]
&=&\left( a^{2}+a\right) {\dot V}_{1} \\[ 5pt ]
&=&- {\dot V}_{1} \left( ∵a+a^{2}+1=0\right) \\[ 5pt ]
&=&-\frac {{\dot Z}_{2}\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} \left( ∵⑬\right) \\[ 5pt ]
&=&-\frac {\mathrm {j}0.015\times 1}{\mathrm {j}0.02+\mathrm {j}0.015} \\[ 5pt ]
&=&-0.428 \ 57 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,距離リレーに入力される各相の電圧値\( \ {\dot V}_{Rb} \ \mathrm {[p.u.]} \ \)及び\( \ {\dot V}_{Rc} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{Rb} &=&{\dot V}_{b}+\frac {\mathrm {j}XL_{S1}}{2}\cdot \frac {{\dot I}_{b}}{2} \\[ 5pt ]
&=&-0.428 \ 57 +\mathrm {j}0.01 \times \frac {-49.487}{2} \\[ 5pt ]
&≒&-0.428 \ 57 -\mathrm {j}0.247 \ 44 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot V}_{Rc} &=&{\dot V}_{c}+\frac {\mathrm {j}XL_{S2}}{2}\cdot \frac {{\dot I}_{c}}{2} \\[ 5pt ]
&=&-0.428 \ 57 +\mathrm {j}0.01 \times \frac {49.487}{2} \\[ 5pt ]
&≒&-0.428 \ 57 +\mathrm {j}0.247 \ 44 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,どちらもボルト\( \ \mathrm {[V]} \ \)で表すと,
\[
\begin{eqnarray}
{\dot V}_{Rb} &=&\frac {77\times 10^{3}}{\sqrt {3}}\left( -0.428 \ 57 -\mathrm {j}0.247 \ 44\right) \\[ 5pt ]
&≒&-19 \ 052 -\mathrm {j}11 \ 000 \ \mathrm {[V]} → -19.1 -\mathrm {j}11.0 \ \mathrm {[kV]} \\[ 5pt ]
{\dot V}_{Rc} &=&\frac {77\times 10^{3}}{\sqrt {3}}\left( -0.428 \ 57 +\mathrm {j}0.247 \ 44\right) \\[ 5pt ]
&≒&-19 \ 052 +\mathrm {j}11 \ 000 \ \mathrm {[V]} → -19.1+\mathrm {j}11.0 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。さらに,\( \ \mathrm {a} \ \)相が見る電圧値\( \ {\dot V}_{Ra} \ \mathrm {[kV]} \ \)及び電流値\( \ {\dot I}_{Ra} \ \mathrm {[A]} \ \)は,\( \ {\dot I}_{a}=0 \ \mathrm {[A]} \ \)より,
\[
\begin{eqnarray}
{\dot I}_{Ra} &=&{\dot I}_{a} \\[ 5pt ]
&=&0 \ \mathrm {[A]} \\[ 5pt ]
{\dot V}_{Ra} &=&{\dot V}_{a} \\[ 5pt ]
&=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
&=&0+\frac {{\dot Z}_{2}\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} +\frac {{\dot Z}_{2}\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} \left( ∵⑬\right) \\[ 5pt ]
&=&\frac {2{\dot Z}_{2}\dot E}{{\dot Z}_{1}+{\dot Z}_{2}} \\[ 5pt ]
&=&\frac {2\times \mathrm {j}0.015\times 1}{\mathrm {j}0.02+\mathrm {j}0.015} \\[ 5pt ]
&≒&0.857 \ 14 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,ボルト\( \ \mathrm {[V]} \ \)で表すと,
\[
\begin{eqnarray}
{\dot V}_{Ra} &=&\frac {77\times 10^{3}}{\sqrt {3}}\times 0.857 \ 14 \\[ 5pt ]
&≒&38 \ 105 \ \mathrm {[V]} → 38.1 \ \mathrm {[kV]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \mathrm {B} \ \)相の距離リレーがみるインピーダンスを求め,リレーの動作範囲内にあるかを判定
題意より,\( \ \mathrm {B} \ \)相の距離リレーがみるインピーダンス\( \ {\dot Z}_{B} \ \mathrm {[\Omega ]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{B} &=&\frac {{\dot V}_{Rb}-{\dot V}_{Rc}}{{\dot I}_{Rb}-{\dot I}_{Rc}} \\[ 5pt ]
&=&\frac {-19 \ 052 -\mathrm {j}11 \ 000-\left( -19 \ 052 +\mathrm {j}11 \ 000\right) }{-1 \ 855.3-1 \ 855.3} \\[ 5pt ]
&=&\frac {-\mathrm {j}22 \ 000}{-3 \ 710.6} \\[ 5pt ]
&≒&\mathrm {j}5.929 \ 0 → \mathrm {j}5.93 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
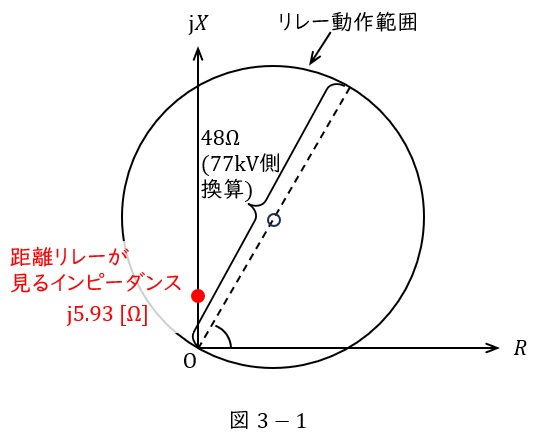
と求められ,図に示すと図3-1のようになり,リレーの動作範囲内であることがわかる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん