【問題】
【難易度】★★★★☆(やや難しい)
制御対象の伝達関数が,\( \ \displaystyle G\left( s\right) =\frac {3}{s+2} \ \)と与えられているとき,以下の問に答えよ。
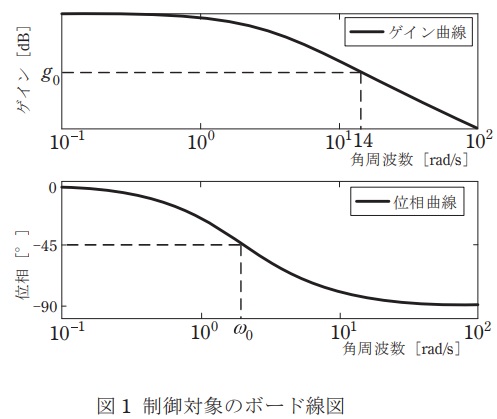
(1) 制御対象の伝達関数\( \ \displaystyle G\left( s\right) =\frac {3}{s+2} \ \)の周波数特性をあらわすボード線図の概略図が図1のようにあらわされている。この図のゲイン\( \ g_{0} \ \mathrm {[dB]} \ \),角周波数\( \ \omega _{0} \ \mathrm {[rad /s]} \ \)に入る値を答えよ。ただし,ゲイン曲線は,\( \ \mathrm {dB} \ \)(デシベル)表示するものとし,横軸の角周波数\( \ \mathrm {[rad /s]} \ \)は,対数目盛で表示する場合を考える。なお,\( \ \log _{10}2 =0.3010 \ \),\( \ \log _{10}3 =0.4771 \ \)とする。
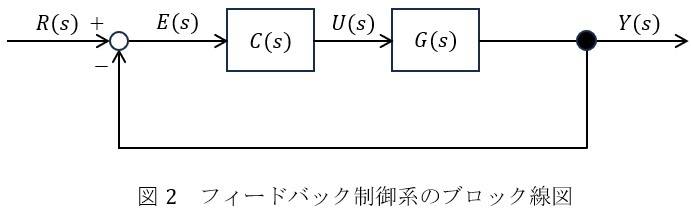
(2) 制御対象\( \ G \left( s\right) \ \)に対して,図2に示すフィードバック制御系を構成する。\( \ C \left( s\right) \ \)は制御器の伝達関数である。また,\( \ R \left( s\right) \ \)は目標値,\( \ Y \left( s\right) \ \)は制御量,\( \ E \left( s\right) \ \)は制御偏差,\( \ U \left( s\right) \ \)は操作量であり,時間信号\( \ r \left( t\right) \ \),\( \ y \left( t\right) \ \),\( \ e \left( t\right) \ \),\( \ u \left( t\right) \ \)をそれぞれラプラス変換したものである。
図2のフィードバック制御系の制御器を\( \ C \left( s\right) =K \ \)とするとき,目標値\( \ R \left( s\right) \ \)から閉ループ出力\( \ Y \left( s\right) \ \)までの閉ループ伝達関数\( \ G_{\mathrm {c}} \left( s\right) \ \)を求めよ。
(3) (2)で求めた閉ループ伝達関数\( \ G_{\mathrm {c}} \left( s\right) \ \)に対して,位相が\( \ -45° \ \)となる角周波数を\( \ \omega _{1} \ \)とする。このとき,\( \ \displaystyle \left| G_{\mathrm {c}} \left( \mathrm {j}\omega _{1}\right) \right| =\frac {0.9}{\sqrt {2}}\ \)となる制御器\( \ C \left( s\right) =K \ \),および角周波数\( \ \omega _{1} \ \)を求めよ。
(4) 図2のフィードバック制御系の制御器を\( \ C \left( s\right) =K \ \)の代りに\( \ \displaystyle C \left( s\right) =\frac {1}{\left( s+1\right) ^{2}} \ \)と設定する。この新しく設定された制御器\( \ C \left( s\right) \ \)に対する一巡伝達関数を\( \ G_{\mathrm {a}} \left( s\right) \ \)とするとき,一巡伝達関数\( \ G_{\mathrm {a}} \left( s\right) \ \)の位相が\( \ -180° \ \)となる角周波数\( \ \omega _{2} \ \)を求めよ。
(5) (4)と同様に図2のフィードバック制御系の制御器を\( \ \displaystyle C \left( s\right) =\frac {1}{\left( s+1\right) ^{2}} \ \)と設定する。このとき得られたフィードバック制御系のゲイン余裕を求めよ。
【ワンポイント解説】
フィードバック制御系のゲインや角周波数を検討する問題です。
じっくりと考えれば解ける問題ですが,計算量や作業量が多く,時間的にかなり厳しい問題と言えるかと思います。
ただし,本問で扱う内容は自動制御で重要な内容ばかりなので,学習教材としてはとても良い問題かと思います。
1.ブロック線図の考え方
①直列
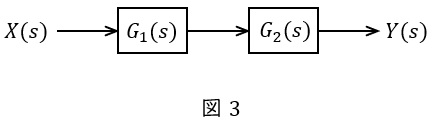
図3のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
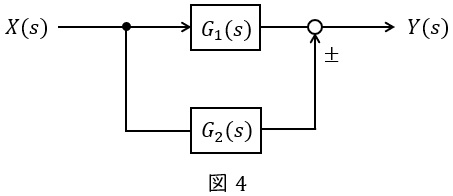
②並列
図4のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
③フィードバック
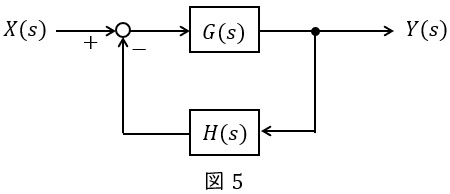
図5のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.一次遅れ要素の伝達関数
\( \ \displaystyle G\left( s\right) =\frac {K}{1+Ts} \ \)で表される伝達関数を一次遅れ要素の伝達関数といい,\( \ K \ \)をゲイン定数,\( \ T \ \)を時定数といいます。
このとき\( \ s→\mathrm {j}\omega \ \)とすれば,周波数伝達関数が\( \ \displaystyle W(\mathrm {j}\omega ) =\frac {K}{1+\mathrm {j}\omega T} \ \)となり,ゲイン\( \ g \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| W(\mathrm {j}\omega )\right| \\[ 5pt ]
&=&20\log _{10} \frac {K}{\sqrt {1+\left( \omega T\right) ^{2}}} \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
となりますが,\( \ \displaystyle \omega \ll \frac {1}{T} \ \)すなわち\( \ \omega T \ll 1 \ \)のとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {1+0}} \\[ 5pt ]
&=&20\log _{10}K \\[ 5pt ]
\end{eqnarray}
\]
とほぼ一定の値となり,\( \ \displaystyle \omega \gg \frac {1}{T} \ \)すなわち\( \ \omega T \gg 1 \ \)のとき,
\[
\begin{eqnarray}
g&≃&20\log _{10} \frac {K}{\sqrt {\left( \omega T\right) ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {K}{\omega T} \\[ 5pt ]
&=&20\log _{10} K-20\log _{10}\omega T \\[ 5pt ]
\end{eqnarray}
\]
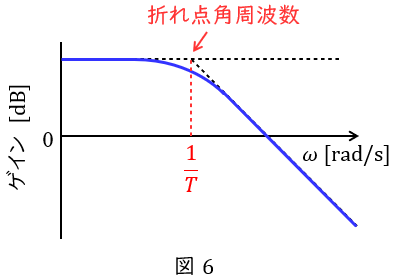
となり,横軸に対数座標をとると,ほぼ直線的に減少していくことになります。これをボード線図といい,図6のようになります。
図6において\( \ \displaystyle \omega =\frac {1}{T} \ \)となる角周波数を折れ点角周波数と呼びます。
3.システムの安定性と速応性
システムの安定性と速応性は,読んで字のごとくどれだけシステムが安定しているか,どれだけ速く応答するかの指標です。ゲイン余裕や位相余裕,ゲイン交差角周波数や位相交差角周波数は,開ループ周波数伝達関数を用いたボード線図とナイキスト線図により理解することができます。
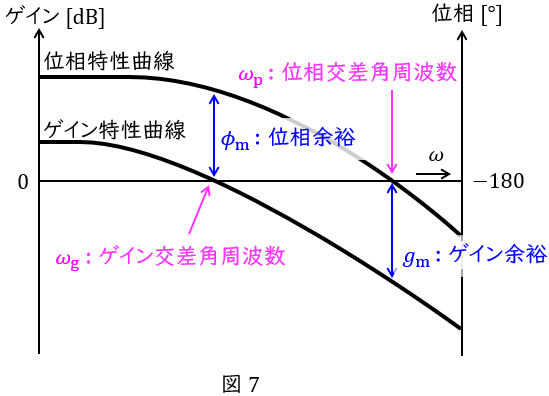
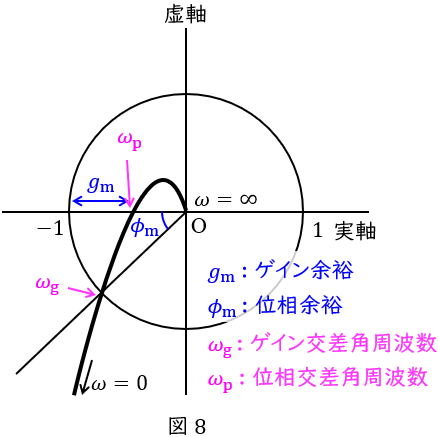
ボード線図は,横軸に角周波数,縦軸にゲインと位相の二軸としたグラフで図7のように描くことができ,ナイキスト線図は実軸と虚軸の平面において,角周波数を\( \ 0 \ \)から\( \ \infty \ \)まで変化させたときのベクトル軌跡で図8のように描くことができます。
安定性の仕様を与える尺度としてはゲイン余裕\( \ g_{\mathrm {m}} \ \)と位相余裕\( \ \phi _{\mathrm {m}} \ \)があり,ゲイン余裕は位相が\( \ -180 \ [°] \ \)のときの\( \ 0 \ \mathrm {[dB]} \ \)との差で,位相余裕はゲインが\( \ 0 \ \mathrm {[dB]} \ \)のときの\( \ -180 \ [°] \ \)との位相差となります。ボード線図とナイキスト線図においては図7及び図8に示すような相互関係があります。
速応性の仕様を与える尺度としてはゲイン交差角周波数\( \ \omega _{\mathrm {g}} \ \)と位相交差角周波数\( \ \omega _{\mathrm {p}} \ \)があり,ゲイン交差角周波数はゲインが\( \ 0 \ \mathrm {[dB]} \ \)のときの角周波数,位相交差角周波数は位相が\( \ -180 \ [°] \ \)のときの角周波数となります。ボード線図とナイキスト線図においては図7及び図8に示すような相互関係になります。
【解答】
(1)図のゲイン\( \ g_{0} \ \mathrm {[dB]} \ \),角周波数\( \ \omega _{0} \ \mathrm {[rad /s]} \ \)に入る値
\( \ \displaystyle G\left( s\right) =\frac {3}{s+2} \ \)の周波数伝達関数は\( \ \displaystyle G\left( \mathrm {j}\omega \right) =\frac {3}{2+\mathrm {j}\omega } \ \)であるから,ゲイン\( \ g \ \mathrm {[dB]} \ \)は,ワンポイント解説「2.一次遅れ要素の伝達関数」の通り,
\[
\begin{eqnarray}
g&=&20\log _{10} \left| G\left( \mathrm {j}\omega \right) \right| \\[ 5pt ]
&=&20\log _{10} \left| \frac {3}{2+\mathrm {j}\omega } \right| \\[ 5pt ]
&=&20\log _{10} \frac {3}{\sqrt {4+\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,図1に沿って,\( \ \omega =14 \ \mathrm {[rad /s]} \ \)を代入すると,求めるゲイン\( \ g_{0} \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g_{0}&=&20\log _{10} \frac {3}{\sqrt {4+14 ^{2}}} \\[ 5pt ]
&=&20\log _{10} \frac {3}{\sqrt {200}} \\[ 5pt ]
&=&20\log _{10} 3-20\log _{10} \sqrt {200} \\[ 5pt ]
&=&20\log _{10} 3-20\times \frac {1}{2}\log _{10} 200 \\[ 5pt ]
&=&20\log _{10} 3-20\times \frac {1}{2}\left( \log _{10} 2+\log _{10} 100\right) \\[ 5pt ]
&=&20\times 0.477 \ 1-20\times \frac {1}{2}\times \left( 0.3010+2 \right) \\[ 5pt ]
&=&-13.468 → -13.5 \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ \displaystyle G\left( \mathrm {j}\omega \right) \ \)を式変形すると,
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) &=&\frac {3}{2+\mathrm {j}\omega } \\[ 5pt ]
&=&\frac {3}{2+\mathrm {j}\omega }\times \frac {2-\mathrm {j}\omega }{2-\mathrm {j}\omega } \\[ 5pt ]
&=&\frac {3}{4+\omega ^{2}}\left( 2-\mathrm {j}\omega \right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,図1における位相が\( \ -45 \ ° \ \)のときの角周波数\( \ \omega _{0} \ \mathrm {[rad /s]} \ \)は,
\[
\begin{eqnarray}
\tan \left( -45°\right) &=&-\frac {\omega _{0}}{2} \\[ 5pt ]
-1 &=&-\frac {\omega _{0}}{2} \\[ 5pt ]
\omega _{0}&=&2 \ \mathrm {[rad /s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)目標値\( \ R \left( s\right) \ \)から閉ループ出力\( \ Y \left( s\right) \ \)までの閉ループ伝達関数\( \ G_{\mathrm {c}} \left( s\right) \ \)
ワンポイント解説「1.ブロック線図の考え方」の通り,\( \ R \left( s\right) \ \)から\( \ Y \left( s\right) \ \)までの閉ループ伝達関数\( \ G_{\mathrm {c}} \left( s\right) \ \)は,
\[
\begin{eqnarray}
G_{\mathrm {c}} \left( s\right) &=&\frac {C \left( s\right) G \left( s\right) }{1+C \left( s\right) G \left( s\right) } \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ C \left( s\right) =K \ \)及び\( \ \displaystyle G\left( s\right) =\frac {3}{s+2} \ \)を代入して整理すると,
\[
\begin{eqnarray}
G_{\mathrm {c}} \left( s\right) &=&\frac {\displaystyle K\cdot \frac {3}{s+2} }{1+\displaystyle K\cdot \frac {3}{s+2}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {3K}{s+2} }{\displaystyle \frac {s+2}{s+2} +\frac {3K}{s+2}} \\[ 5pt ]
&=&\frac {3K}{s+2+3K} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \displaystyle \left| G_{\mathrm {c}} \left( \mathrm {j}\omega _{1}\right) \right| =\frac {0.9}{\sqrt {2}} \ \)となる制御器\( \ C \left( s\right) =K \ \),および角周波数\( \ \omega _{1} \ \)
\( \ G_{\mathrm {c}} \left( s\right) \ \)の周波数伝達関数は\( \ \displaystyle G_{\mathrm {c}} \left( \mathrm {j}\omega \right) =\frac {3K}{2+3K+\mathrm {j}\omega } \ \)となるので,(1)と同様に考えると位相が\( \ -45 \ ° \ \)のときの角周波数\( \ \omega _{1} \ \mathrm {[rad /s]} \ \)と\( \ K \ \)との関係は,
\[
\begin{eqnarray}
-1 &=&-\frac {\omega _{1} }{2+3K} \\[ 5pt ]
2+3K&=&\omega _{1} ・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさ\( \ \displaystyle \left| G_{\mathrm {c}} \left( \mathrm {j}\omega _{1}\right) \right| =\frac {0.9}{\sqrt {2}} \ \)より,
\[
\begin{eqnarray}
\left| G_{\mathrm {c}} \left( \mathrm {j}\omega _{1}\right) \right| &=&\frac {3K}{\sqrt {\left( 2+3K\right) ^{2}+\omega _{1}^{2}}} \\[ 5pt ]
\frac {0.9}{\sqrt {2}} &=&\frac {\omega _{1}-2}{\sqrt {\omega _{1}^{2}+\omega _{1}^{2}}} \\[ 5pt ]
\frac {0.9}{\sqrt {2}} &=&\frac {\omega _{1}-2}{\sqrt {2}\omega _{1}} \\[ 5pt ]
0.9 &=&\frac {\omega _{1}-2}{\omega _{1}} \\[ 5pt ]
0.9\omega _{1} &=&\omega _{1}-2 \\[ 5pt ]
0.1\omega _{1} &=&2 \\[ 5pt ]
\omega _{1} &=&20 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められ,さらにこれを①に代入すれば,
\[
\begin{eqnarray}
2+3K&=&\omega _{1} \\[ 5pt ]
&=&20 \\[ 5pt ]
3K&=&18 \\[ 5pt ]
K&=&6 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)一巡伝達関数\( \ G_{\mathrm {a}} \left( s\right) \ \)の位相が\( \ -180° \ \)となる角周波数\( \ \omega _{2} \ \)
図2の一巡伝達関数\( \ G_{\mathrm {a}} \left( s\right) \ \)は,
\[
\begin{eqnarray}
G_{\mathrm {a}} \left( s\right) &=&C \left( s\right) G \left( s\right) \\[ 5pt ]
&=&\frac {1}{\left( s+1\right) ^{2}}\cdot \frac {3}{s+2} \\[ 5pt ]
&=&\frac {1}{s^{2}+2s+1}\cdot \frac {3}{s+2} \\[ 5pt ]
&=&\frac {3}{s^{3}+4s^{2}+5s+2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ G_{\mathrm {a}} \left( s\right) \ \)の周波数伝達関数\( \ G_{\mathrm {a}} \left( \mathrm {j}\omega \right) \ \)は,
\[
\begin{eqnarray}
G_{\mathrm {a}} \left( \mathrm {j}\omega \right) &=&\frac {3}{\left( \mathrm {j}\omega \right) ^{3}+4\left( \mathrm {j}\omega \right) ^{2}+\mathrm {j}5\omega +2} \\[ 5pt ]
&=&\frac {3}{2-4\omega ^{2}+\mathrm {j}\left( 5\omega -\omega ^{3} \right) } \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,位相が\( \ -180° \ \)となる角周波数\( \ \omega _{2} \ \mathrm {[rad / s]} \ \)は,上式の虚部が零であれば良いので,\( \ \omega > 0 \ \)に注意すれば,
\[
\begin{eqnarray}
5\omega _{2}-\omega _{2} ^{3} &=&0 \\[ 5pt ]
5-\omega _{2} ^{2} &=&0 \\[ 5pt ]
\omega _{2} ^{2} &=&5 \\[ 5pt ]
\omega _{2} &=&\sqrt {5} → 2.24 \ \mathrm {[rad / s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)フィードバック制御系のゲイン余裕
ワンポイント解説「3.システムの安定性と速応性」の通り,ゲイン余裕は位相が\( \ -180° \ \)のときの\( \ 0 \ \mathrm {[dB]} \ \)とゲインの差なので,角周波数\( \ \omega _{2}=\sqrt {5} \ \mathrm {[rad / s]} \ \)のときのゲインの差を求めれば良い。したがって,ゲイン余裕\( \ g_{\mathrm {m}} \ \mathrm {[dB]} \ \)は,
\[
\begin{eqnarray}
g_{\mathrm {m}} &=&0-20\log _{10} \left| G_{\mathrm {a}} \left( \mathrm {j}\omega _{2} \right) \right| \\[ 5pt ]
&=&-20\log _{10} \left| \frac {3}{2-4\omega _{2}^{2}+\mathrm {j}\left( 5\omega _{2}-\omega _{2}^{3} \right) } \right| \\[ 5pt ]
&=&-20\log _{10} \left| \frac {3}{2-4\left( \sqrt {5}\right) ^{2}+\mathrm {j}\left\{ 5\sqrt {5}-\left( \sqrt {5}\right) ^{3} \right\} } \right| \\[ 5pt ]
&=&-20\log _{10} \left| \frac {3}{-18+\mathrm {j}0 } \right| \\[ 5pt ]
&=&-20\log _{10} \frac {1}{6} \\[ 5pt ]
&=&20\log _{10} 6 \\[ 5pt ]
&=&20\times \left( \log _{10} 2+\log _{10} 3\right) \\[ 5pt ]
&=&20\times \left( 0.301 \ 0+0.477 \ 1 \right) \\[ 5pt ]
&=&15.562 → 15.6 \ \mathrm {[dB]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん