《理論》〈電磁気〉[H20:問1]直線上に配置された不等量異符号の点電荷による電位及び電界に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，直線上に配置された不等量異符号の点電荷による電位及び電界に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる式を解答群の中から選び，その記号をマークシートに記入しなさい。なお，真空の誘電率を$ \ \varepsilon _{0} \ $とする。

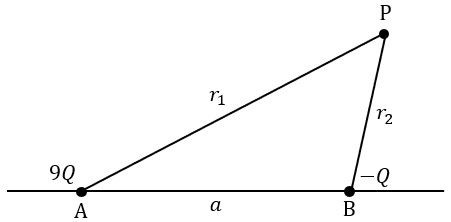
真空中で，図のように直線上の点$ \ \mathrm {A} \ $，点$ \ \mathrm {B} \ $にそれぞれ点電荷$ \ 9Q \ $と$ \ -Q \ $が配置されている。$ \ \mathrm {AB} \ $間の距離を$ \ a \ $とする。点$ \ \mathrm {A} \ $から$ \ r_{1} \ $，点$ \ \mathrm {B} \ $から$ \ r_{2} \ $の距離にある点$ \ \mathrm {P} \ $における電位$ \ V_{P} \ $は$ \ \fbox {　（１）　} \ $である。したがって，$ \ \fbox {　（２）　} \ $の条件が成り立つ点の電位は零となる。

一方，電界が零となる点を$ \ \mathrm {D} \ $とすると，点$ \ \mathrm {D} \ $は点$ \ \mathrm {A} \ $，点$ \ \mathrm {B} \ $を通る直線上にあり，$ \ \mathrm {AD} \ $間距離は$ \ \fbox {　（３）　} \ $，$ \ \mathrm {BD} \ $間距離は$ \ \fbox {　（４）　} \ $である。これより，点$ \ \mathrm {D} \ $の電位$ \ V_{D} \ $は$ \ \fbox {　（５）　} \ $となる。

〔問1の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {Q}{4\pi \varepsilon _{0}}\left( \frac {9}{r_{1}}-\frac {1}{r_{2}}\right)　　　　　&（ロ）&　\frac {r_{1}}{r_{2}}=-9　　　　　&（ハ）&　-\frac {3a}{4} \\[ 5pt ] &（ニ）&　-\frac {a}{4}　　　　　　　&（ホ）&　\frac {a}{4}　　　　　&（ヘ）&　\frac {r_{1}}{r_{2}}=9 \\[ 5pt ] &（ト）&　\frac {3a}{2}　　　　　&（チ）&　\frac {a}{2}　　　　　　　&（リ）&　\frac {Q}{\pi \varepsilon _{0}a^{2}} \\[ 5pt ] &（ヌ）&　\frac {3a}{4}　　　　　&（ル）&　\frac {Q}{4\pi \varepsilon _{0}}\left( \frac {9}{r_{1}^{2}}-\frac {1}{r_{2}^{2}}\right)　　　　　　&（ヲ）&　\frac {Q}{\pi \varepsilon _{0}a} \\[ 5pt ] &（ワ）&　\frac {2Q}{\pi \varepsilon _{0}a}　　　　　&（カ）&　\frac {r_{1}}{r_{2}}=3　　　　　　&（ヨ）&　\frac {Q}{4\pi \varepsilon _{0}}\left( \frac {9}{r_{1}}+\frac {1}{r_{2}}\right) \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

電荷量の異なる電荷を置いたときの電位や電界を考える問題です。
$ \ 1 \ $種としてはかなり解きやすい問題なので，多くの受験生が完答をできた問題かと思います。
本問で扱う内容はいずれも$ \ 3 \ $種から学習している内容なので，必ず理解しておきましょう。

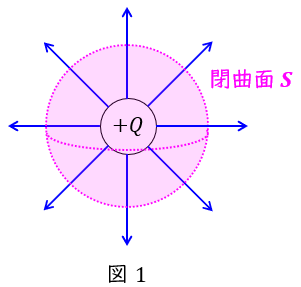
1.ガウスの法則
$ \ Q \ \mathrm {[C]} \ $から出る電気力線は$ \ \displaystyle \frac {Q}{\varepsilon } \ $本，電束は$ \ Q \ $本であり，電界$ \ E \ \mathrm {[V / m]} \ $及び電束密度$ \ D \ \mathrm {[C / m^{2}]} \ $との関係は，任意の閉曲面において，
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ] \int _{S} \boldsymbol D \cdot \mathrm {d}\boldsymbol S &=& Q \\[ 5pt ] \end{eqnarray}
\] となり，これをガウスの法則といいます。閉曲面が球で，点電荷に蓄えられている電荷$ \ Q \ \mathrm {[C]} \ $があれば，電界$ \ E \ \mathrm {[V / m]} \ $は，
\[
\begin{eqnarray}
4\pi r^{2} \cdot E &=& \frac {Q}{\varepsilon } \\[ 5pt ] E &=& \frac {Q}{4\pi \varepsilon r^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。

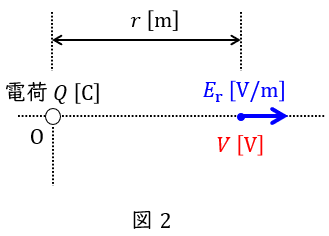
2.空間上の電位$ \ V \ $
中心からの距離$ \ r \ \mathrm {[m]} \ $に関する電界$ \ E_{\mathrm {r}} \ \mathrm {[V / m]} \ $が与えられている時，その場所の電位$ \ V \ \mathrm {[V]} \ $は無限遠を基準とすると，
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E_{\mathrm {r}}\mathrm {d}r \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)解答：イ
一般に点電荷$ \ Q \ $から$ \ r \ $離れた場所の電位$ \ V \ $は無限遠を基準とすると，ワンポイント解説「2.空間上の電位$ \ V \ $」の通り，
\[
\begin{eqnarray}
V&=&-\int _{\infty }^{r}E\mathrm {d}r \\[ 5pt ] &=&-\int _{\infty }^{r}\frac {Q}{4\pi \varepsilon _{0}r^{2}}\mathrm {d}r \\[ 5pt ] &=&-\frac {Q}{4\pi \varepsilon _{0}}\int _{\infty }^{r}\frac {1}{r^{2}}\mathrm {d}r \\[ 5pt ] &=&-\frac {Q}{4\pi \varepsilon _{0}}\left[ -\frac {1}{r}\right] _{\infty }^{r} \\[ 5pt ] &=&-\frac {Q}{4\pi \varepsilon _{0}}\left( -\frac {1}{r}\right) \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}r} \\[ 5pt ] \end{eqnarray}
\] となるので，点$ \ \mathrm {P} \ $における電位$ \ V_{P} \ $は，
\[
\begin{eqnarray}
V_{P}&=&\frac {9Q}{4\pi \varepsilon r_{1}}-\frac {Q}{4\pi \varepsilon _{0}r_{2}} \\[ 5pt ] &=&\frac {Q}{4\pi \varepsilon _{0}}\left( \frac {9}{r_{1}}-\frac {1}{r_{2}}\right) \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヘ
(1)解答式より，電位が零となるのは，
\[
\begin{eqnarray}
\frac {Q}{4\pi \varepsilon _{0}}\left( \frac {9}{r_{1}}-\frac {1}{r_{2}}\right) &=&0 \\[ 5pt ] \frac {9}{r_{1}}-\frac {1}{r_{2}}&=&0 \\[ 5pt ] \frac {9}{r_{1}}&=&\frac {1}{r_{2}} \\[ 5pt ] \frac {r_{1}}{r_{2}}&=&9 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ト
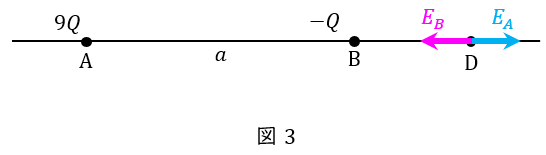
電界の向きは，点電荷$ \ 9Q \ $からは電気力線が出て，点電荷$ \ -Q \ $には電気力線が入る方向であるため，電界が零となる点$ \ \mathrm {D} \ $は図3に示すように直線$ \ \mathrm {AB} \ $上の右側の点となる。
$ \ \mathrm {BD} \ $間距離を$ \ r \ $とすると，点$ \ \mathrm {D} \ $における電界の大きさ$ \ E \ $を求める式より，
\[
\begin{eqnarray}
E = \frac {9Q}{4\pi \varepsilon _{0}\left( a+r\right) ^{2}}-\frac {Q}{4\pi \varepsilon _{0}r^{2}}&=&0 \\[ 5pt ] \frac {9Q}{4\pi \varepsilon _{0}\left( a+r\right) ^{2}}&=&\frac {Q}{4\pi \varepsilon _{0}r^{2}} \\[ 5pt ] \frac {9}{\left( a+r\right) ^{2}}&=&\frac {1}{ r^{2}} \\[ 5pt ] \frac {3}{a+r}&=&\frac {1}{ r} \\[ 5pt ] 3r&=&a+r \\[ 5pt ] 2r&=&a \\[ 5pt ] r&=&\frac {a}{2} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ \mathrm {AD} \ $間距離は$ \ \displaystyle a+\frac {a}{2}=\frac {3a}{2} \ $と求められる。

(4)解答：チ
(3)解答式より，$ \ \mathrm {BD} \ $間距離は$ \ \displaystyle \frac {a}{2} \ $と求められる。

(5)解答：ヲ
(3)及び(4)解答より，点$ \ \mathrm {D} \ $の電位$ \ V_{D} \ $は，
\[
\begin{eqnarray}
V_{P}&=&\frac {9Q}{\displaystyle 4\pi \varepsilon _{0} \frac {3a}{2}}-\frac {Q}{\displaystyle 4\pi \varepsilon _{0} \frac {a}{2}} \\[ 5pt ] &=&\frac {3Q}{\displaystyle 2\pi \varepsilon _{0} a}-\frac {Q}{\displaystyle 2\pi \varepsilon _{0} a} \\[ 5pt ] &=&\frac {2Q}{\displaystyle 2\pi \varepsilon _{0} a} \\[ 5pt ] &=&\frac {Q}{\displaystyle \pi \varepsilon _{0} a} \\[ 5pt ] \end{eqnarray}
\] と求められる。