【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,直流回路の電流計算(等価変換)に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
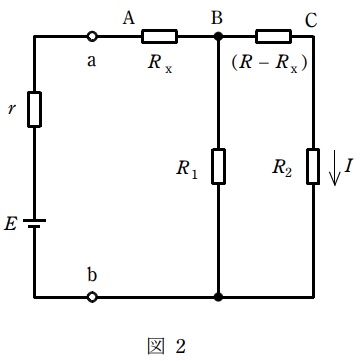
図1において,抵抗\( \ R_{2} \ \)に流れる電流\( \ I \ \)が最小になる条件を求めたい。ただし,図の可変抵抗\( \ \mathrm {A}-\mathrm {C} \ \)間の抵抗を\( \ R \ \),\( \ \mathrm {A}-\mathrm {B} \ \)間の抵抗を\( \ R_{\mathrm {x}} \ \),\( \ \mathrm {B}-\mathrm {C} \ \)間の抵抗を\( \ \left( R-R_{\mathrm {x}}\right) \ \)とする。
まず,図1の端子\( \ \mathrm {a}-\mathrm {b} \ \)より左側部分を図2に示す抵抗\( \ r \ \)と電圧源\( \ E \ \)に等価変換すると,それぞれ\( \ r=\fbox { (1) } \ \mathrm {[\Omega ]} \),\( \ E=\fbox { (2) } \ \mathrm {[V]} \ \)となる。
ところで,図2について考えると,\( \ R_{2} \ \)に流れる電流\( \ I \ \)は,
\[
\begin{eqnarray}
I &=& \frac {R_{1}E}{\fbox { (3) }+R_{1}\left( R_{2}+R\right) +r\left( R_{1}+R_{2}+R\right) } ・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,電流\( \ I \ \)が最小になる条件は①式の分母が最大の場合であるから,\( \ R_{\mathrm {x}}=\fbox { (4) } \ \)となるように可変抵抗を調整した場合に電流が最小となる。このとき,\( \ \left( r+R_{\mathrm {x}}\right) \ \)と\( \ \left( R-R_{\mathrm {x}}+R_{2}\right) \ \)の関係は,\( \ \left( r+R_{\mathrm {x}}\right) \ \fbox { (5) } \ \left( R-R_{\mathrm {x}}+R_{2}\right) \ \)となる。ただし,\( \ \left( R_{2}+R\right) > r \ \)であるとする。

〔問2の解答群〕
\[
\begin{eqnarray}
&(イ)& R_{2}+R-r &(ロ)& > &(ハ)& = \\[ 5pt ]
&(ニ)& 4.5 &(ホ)& 21 &(ヘ)& R_{\mathrm {x}}\left( R_{2}+R-r-R_{\mathrm {x}}\right) \\[ 5pt ]
&(ト)& 2 &(チ)& 9 &(リ)& R_{\mathrm {x}}\left( R_{1}+R_{2}+R-r-R_{\mathrm {x}}\right) \\[ 5pt ]
&(ヌ)& < &(ル)& \frac {R_{2}+R-r}{2} &(ヲ)& \frac {R_{1}+R_{2}+R-r}{2} \\[ 5pt ]
&(ワ)& 1 &(カ)& 24 &(ヨ)& R_{\mathrm {x}}\left( R_{2}+R-r\right) \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
3種から定番である等価変換を用いた問題です。(3)の計算がやや面倒ですが,主だって難しい内容はありません。
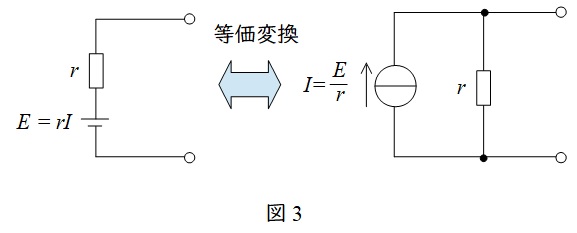
1.電圧源と電流源の等価変換
図3に示すように,電圧源と電流源は直列と並列で等価変換することができます。
【関連する「電気の神髄」記事】
【解答】
(1)解答:チ
(2)解答:ホ
ワンポイント解説「1.電圧源と電流源の等価変換」の通り,図1の電流源を電圧源に等価変換した時の電圧の大きさを\( \ E_{0} \ \)とすると,
\[
\begin{eqnarray}
E_{0} &=&3\times 7.5 \\[ 5pt ]
&=&22.5 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \mathrm {a}-\mathrm {b} \ \)の左側の回路はすべて直列となるから,
\[
\begin{eqnarray}
r &=&3+6 \\[ 5pt ]
&=&9 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
E &=&E_{0}-1.5 \\[ 5pt ]
&=&22.5-1.5 \\[ 5pt ]
&=&21 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヘ
直並列の合成抵抗及び分流の法則より,\( \ R_{2} \ \)を流れる電流\( \ I \ \)は,
\[
\begin{eqnarray}
I &=&\frac {E}{\displaystyle \left( r+R_{\mathrm {x}}\right) +\frac {R_{1}\left[ \left( R-R_{\mathrm {x}}\right) +R_{2}\right] }{R_{1}+\left[ \left( R-R_{\mathrm {x}}\right) +R_{2}\right] }}\times \frac {R_{1}}{R_{1}+\left[ \left( R-R_{\mathrm {x}}\right) +R_{2}\right] } \\[ 5pt ]
&=&\frac {R_{1}E}{\displaystyle \left( r+R_{\mathrm {x}}\right) \left( R_{1}+R-R_{\mathrm {x}} +R_{2}\right) +R_{1}\left( R-R_{\mathrm {x}}+R_{2}\right) } \\[ 5pt ]
&=&\frac {R_{1}E}{r\left( R_{1}+R-R_{\mathrm {x}}+R_{2}\right) +R_{\mathrm {x}}\left( R_{1}+R-R_{\mathrm {x}} +R_{2}\right) +R_{1}\left( R-R_{\mathrm {x}}+R_{2}\right) } \\[ 5pt ]
&=&\frac {R_{1}E}{r\left( R_{1}+R-R_{\mathrm {x}}+R_{2}\right) +R_{\mathrm {x}}\left( R-R_{\mathrm {x}} +R_{2}\right) +R_{1}\left( R+R_{2}\right) } \\[ 5pt ]
&=&\frac {R_{1}E}{R_{\mathrm {x}}\left( R_{2}+R-r-R_{\mathrm {x}} \right) +R_{1}\left( R+R_{2}\right) +r\left( R_{1}+R_{2}+R\right)} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
(3)の解答式の分母を\( \ A=R_{\mathrm {x}}\left( R_{2}+R-r-R_{\mathrm {x}} \right) +R_{1}\left( R+R_{2}\right) +r\left( R_{1}+R_{2}+R\right) \ \)と置く。両辺微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}A}{\mathrm {d}R_{\mathrm {x}}} &=&R_{2}+R-r-2R_{\mathrm {x}} \\[ 5pt ]
\end{eqnarray}
\]
となる。分母が最大となる条件は\( \ \displaystyle \frac {\mathrm {d}A}{\mathrm {d}R_{\mathrm {x}}}=0 \ \)の時であるから,
\[
\begin{eqnarray}
R_{2}+R-r-2R_{\mathrm {x}} &=&0 \\[ 5pt ]
R_{\mathrm {x}} &=&\frac {R_{2}+R-r}{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ハ
(4)の解答式を変形すると,
\[
\begin{eqnarray}
2R_{\mathrm {x}} &=&R_{2}+R-r \\[ 5pt ]
R_{\mathrm {x}}+r &=&R_{2}-R_{\mathrm {x}}+R \\[ 5pt ]
\end{eqnarray}
\]
となるので,両者は等しい関係となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん