【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,電力システムにおける計画・運用のための,計算機システムに組み込まれている潮流計算に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句を解答群の中から選び,その記号を記述用紙の解答欄に記入しなさい。
潮流計算は,電力系統やプラントなどの電力システムの計画・運用に必須な計算技術である。一般に潮流計算は,電力方程式を厳密に解いて,電圧,位相角,有効・無効電力潮流を求める交流法を用いることが多い。この電力方程式では,送電線や変圧器をブランチ,発変電所などの母線をノードとして,アドミタンス行列で表現された電気回路に基づいて構成され,電力システムの場合,非零要素が極めて少ない\( \ \fbox { (1) } \ \)行列となる。一方,この電力方程式の既知量は,そのノードの特性に応じて指定される。一般的には,発電母線に対して有効電力及び電圧を指定するノードを\( \ \mathrm {PV} \ \)指定ノードと呼び,負荷母線に対して有効電力及び無効電力を指定するノードを\( \ \mathrm {PQ} \ \)指定ノードと呼び,さらに,電圧位相角の基準となるノードを\( \ \fbox { (2) } \ \)ノードと呼び,系統の有効・無効電力損失分を充当させている。また,この方程式の電圧座標の取り方に応じて,\( \ \fbox { (3) } \ \)座標又は極座標が使用される。
電力方程式は非線形代数方程式であり,これを解くには未知数に適当な初期値を設定して,反復計算により正解に収束させる必要がある。その代表例として,\( \ \fbox { (4) } \ \)法があり,反復計算する係数として,\( \ \fbox { (5) } \ \)と呼ばれる電力方程式の微分係数を用いて収束計算する方法が著名である。
一方,上述した交流法に対して,電圧の位相角と有効電力潮流の概略値を求める直流法と呼ばれる簡易計算も用いることがある。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& 立 体 &(ロ)& スパース &(ハ)& ルンゲクッタ \\[ 5pt ]
&(ニ)& スラック &(ホ)& 逐次係数 &(ヘ)& オイラー \\[ 5pt ]
&(ト)& ヤコビアン行例 &(チ)& 補 充 &(リ)& フラット \\[ 5pt ]
&(ヌ)& 三 角 &(ル)& インピーダンス &(ヲ)& 加速係数 \\[ 5pt ]
&(ワ)& 直 角 &(カ)& 慣 性 &(ヨ)& ニュートンラフソン \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
計算機システムに組み込まれている潮流計算に関する問題です。
非常に専門性が高く計算機内の内容なので,実務で電力潮流を扱っている方でも厳しい問題であったかなと思います。おそらく選択された受験生は少ないと予想されますので,参考程度に見ておいて下さい。
1.潮流計算に用いる電力方程式
電力潮流は発電所から負荷までどのように電力が流れるかを検討する技術で,電力方程式が用いられることが多いです。電力方程式では,発変電所等の母線をノード,送電線や変圧器をブランチとして,アドミタンス行列で表現されます。
ノードには有効電力,無効電力,電圧,位相角の\( \ 4 \ \)つの変数があり,\( \ 2 \ \)つが既知,残りの二つを未知として計算していきます。
このうち発電母線に対しては発電機で有効電力が調整されており\( \mathrm {AVR} \ \)で電圧を調整できるので\( \ \mathrm {PV} \ \)指定ノード,負荷母線に対しては消費する有効電力と力率によって定まる無効電力が分かるので\( \ \mathrm {PQ} \ \)指定ノードとなります。また,発電母線のうち一つを電圧位相角の基準として,系統の有効・無効電力損失分を充当させるノード,すなわち電圧と位相が定まる基準ノード(スラックノード)とします。
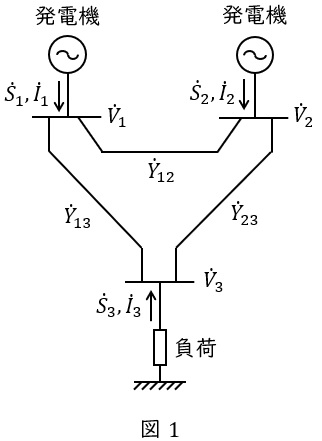
文章で説明しても非常にわかりにくいので,例えば簡易的に令和3年電力管理科目問3で出題された図1に示すような電力系統を考えていきます。母線\( \ 1 \ \)をスラックノードとすると,母線\( \ 2 \ \)は\( \ \mathrm {PV} \ \)指定ノード,母線\( \ 3 \ \)は\( \ \mathrm {PQ} \ \)指定ノードとなります。
各母線間のアドミタンスを図1の通りとすると,図1の各電圧及び電流の関係は,
\[
\begin{eqnarray}
{\dot I}_{1}&=&{\dot Y}_{12}\left( {\dot V}_{1}-{\dot V}_{2}\right) +{\dot Y}_{13}\left( {\dot V}_{1}-{\dot V}_{3}\right) \\[ 5pt ]
&=&\left( {\dot Y}_{12}+{\dot Y}_{13}\right) {\dot V}_{1}-{\dot Y}_{12}{\dot V}_{2}-{\dot Y}_{13}{\dot V}_{3} \\[ 5pt ]
{\dot I}_{2}&=&{\dot Y}_{12}\left( {\dot V}_{2}-{\dot V}_{1}\right) +{\dot Y}_{23}\left( {\dot V}_{2}-{\dot V}_{3}\right) \\[ 5pt ]
&=&-{\dot Y}_{12}{\dot V}_{1}+\left( {\dot Y}_{12}+{\dot Y}_{23}\right) {\dot V}_{2}-{\dot Y}_{23}{\dot V}_{3} \\[ 5pt ]
{\dot I}_{3}&=&{\dot Y}_{13}\left( {\dot V}_{3}-{\dot V}_{1}\right) +{\dot Y}_{23}\left( {\dot V}_{3}-{\dot V}_{2}\right) \\[ 5pt ]
&=&-{\dot Y}_{13}{\dot V}_{1}-{\dot Y}_{23}{\dot V}_{2}+\left( {\dot Y}_{13}+{\dot Y}_{23}\right) {\dot V}_{3} \\[ 5pt ]
\end{eqnarray}
\]
となり,行列の形に整理すると,
\[
\begin{eqnarray}
\begin{bmatrix}
{\dot I}_{1} \\
{\dot I}_{2} \\
{\dot I}_{3} \\
\end{bmatrix}
&=&
\begin{bmatrix}
\displaystyle {\dot Y}_{12}+{\dot Y}_{13} & \displaystyle -{\dot Y}_{12} & \displaystyle -{\dot Y}_{13} \\
\displaystyle -{\dot Y}_{12} & \displaystyle {\dot Y}_{12}+{\dot Y}_{23} & \displaystyle -{\dot Y}_{23} \\
\displaystyle -{\dot Y}_{13} & \displaystyle -{\dot Y}_{23} & \displaystyle {\dot Y}_{13}+{\dot Y}_{23} \\
\end{bmatrix}
\begin{bmatrix}
{\dot V}_{1} \\
{\dot V}_{2} \\
{\dot V}_{3} \\
\end{bmatrix}
\end{eqnarray}
\]
となります。この行列式のうち,
\[
\begin{eqnarray}
\left[ {\dot Y}_{kl}\right]
&=&
\begin{bmatrix}
\displaystyle {\dot Y}_{12}+{\dot Y}_{13} & \displaystyle -{\dot Y}_{12} & \displaystyle -{\dot Y}_{13} \\
\displaystyle -{\dot Y}_{12} & \displaystyle {\dot Y}_{12}+{\dot Y}_{23} & \displaystyle -{\dot Y}_{23} \\
\displaystyle -{\dot Y}_{13} & \displaystyle -{\dot Y}_{23} & \displaystyle {\dot Y}_{13}+{\dot Y}_{23} \\
\end{bmatrix}
\end{eqnarray}
\]
をノードアドミタンス行列といいます。実際の系統においては,ノードの数に対してブランチの数が少ないため,ノードアドミタンス行列の要素は零が非常に多い疎行列(スパース行列)となります。
次に,複素電力\( \ {\dot S}_{k}=P_{k}+\mathrm {j}Q_{k} \ \left( k=1,2,3\right) \ \)とすれば,遅れ無効電力を正とすると,
\[
\begin{eqnarray}
P_{k}+\mathrm {j}Q_{k}&=&{\dot V}_{\mathrm {k}}\overline {\dot I_{k}} \\[ 5pt ]
&=&{\dot V}_{\mathrm {k}}\displaystyle \sum_{l=1}^3 \overline {{\dot Y}_{kl}{\dot V}_{l}} \\[ 5pt ]
\end{eqnarray}
\]
となり,アドミタンス\( \ {\dot Y}_{kl}=G_{kl}+\mathrm {j}B_{kl} \ \)とすれば,
\[
\begin{eqnarray}
{\dot V}_{k}&=&\left| {\dot V}_{k}\right| \left( \cos \theta _{k}+\mathrm {j}\sin \theta _{k}\right) \\[ 5pt ]
\overline {{\dot V}_{l}}&=&\left| {\dot V}_{l}\right| \left( \cos \theta _{l}-\mathrm {j}\sin \theta _{l}\right) \\[ 5pt ]
\overline {{\dot Y}_{kl}}&=&G_{kl}-\mathrm {j}B_{kl} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
P_{k}+\mathrm {j}Q_{k}&=&\left| {\dot V}_{k}\right| \left( \cos \theta _{k}+\mathrm {j}\sin \theta _{k}\right)\displaystyle \sum_{l=1}^3 \left( G_{kl}-\mathrm {j}B_{kl}\right) \left| {\dot V}_{l}\right| \left( \cos \theta _{l}-\mathrm {j}\sin \theta _{l}\right) \\[ 5pt ]
&=&\displaystyle \sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left( \cos \theta _{k}+\mathrm {j}\sin \theta _{k}\right) \left( \cos \theta _{l}-\mathrm {j}\sin \theta _{l}\right) \left( G_{kl}-\mathrm {j}B_{kl}\right) \\[ 5pt ]
&=&\displaystyle \sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left\{ \cos \theta _{k}\cos \theta _{l}+\sin \theta _{k}\sin \theta _{l}+\mathrm {j}\left( \sin \theta _{k}\cos \theta _{l}-\cos \theta _{k}\sin \theta _{l}\right) \right\} \left( G_{kl}-\mathrm {j}B_{kl}\right) \\[ 5pt ]
&=&\displaystyle \sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left\{ \cos \left( \theta _{k}- \theta _{l}\right) +\mathrm {j} \sin \left( \theta _{k}- \theta _{l}\right) \right\} \left( G_{kl}-\mathrm {j}B_{kl}\right) \\[ 5pt ]
&=&\displaystyle \sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left[ G_{kl} \cos \left( \theta _{k}- \theta _{l}\right) +B_{kl}\sin \left( \theta _{k}- \theta _{l}\right) +\mathrm {j} \left\{ G_{kl} \sin \left( \theta _{k}- \theta _{l}\right) -B_{kl}\cos \left( \theta _{k}- \theta _{l}\right) \right\} \right] \\[ 5pt ]
\end{eqnarray}
\]
と整理できるので,\( \ P_{k} \ \)及び\( \ Q_{k} \ \)は,
\[
\begin{eqnarray}
P_{k}&=&\sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left\{ G_{kl} \cos \left( \theta _{k}- \theta _{l}\right) +B_{kl}\sin \left( \theta _{k}- \theta _{l}\right) \right\} \\[ 5pt ]
Q_{k}&=&\sum_{l=1}^3\left| {\dot V}_{k}\right| \left| {\dot V}_{l}\right| \left\{ G_{kl} \sin \left( \theta _{k}- \theta _{l}\right) -B_{kl}\cos \left( \theta _{k}- \theta _{l}\right) \right\} \\[ 5pt ]
\end{eqnarray}
\]
となります。このように各母線の有効電力と無効電力を電圧の大きさと位相で表す式を電力方程式といいます。実際の系統においては,ノードの数がさらに多くなるので,上式はさらに複雑になります。
2.ニュートンラプソン法
電力方程式に基づく変数の計算を繰り返すことで未知の量を求める方法です。図1を例において,以下に示すような偏微分\( \ \displaystyle \frac{ \partial f }{ \partial x } \ \)を成分とするヤコビアン行例と呼ばれる電力方程式の微分係数を用いて収束計算をしていき,誤差が許容値範囲内になる収束判定を満たしたときの値を解とします。
詳細は専門性が高すぎるので割愛しますが,未知の量に適当な数値を入れて既知の量を求め,求められた誤差から未知の量を修正し,繰り返し演算で誤差が許容値以下になる未知の量を推定していくようなイメージで良いかと思います。
\[
\begin{eqnarray}
\left(
\begin{array}{c}
\Delta P_{2} \\
\Delta P_{3} \\
\Delta Q_{3}
\end{array}
\right) &=& \left(
\begin{array}{ccc}
\displaystyle \frac { \partial P_{2} }{ \partial \theta _{2} } & \displaystyle \frac { \partial P_{2} }{ \partial \theta _{3} } & \displaystyle \frac { \partial P_{2} }{ \partial V_{3} } \\
\displaystyle \frac { \partial P_{3} }{ \partial \theta _{2} } & \displaystyle \frac { \partial P_{3} }{ \partial \theta _{3} } & \displaystyle \frac { \partial P_{3} }{ \partial V_{3} } \\
\displaystyle \frac { \partial Q_{3} }{ \partial \theta _{2} } & \displaystyle \frac { \partial Q_{3} }{ \partial \theta _{3} } & \displaystyle \frac { \partial Q_{3} }{ \partial V_{3} } \\
\end{array}
\right)
\left(
\begin{array}{c}
\Delta \theta _{2} \\
\Delta \theta _{3} \\
\Delta V_{3}
\end{array}
\right)
\end{eqnarray}
\]
【解答】
(1)解答:ロ
題意より解答候補は,(ロ)スパース,(ホ)逐次係数,(ヌ)三角,(ル)インピーダンス,(ワ)直角,等になると思います。
ワンポイント解説「1.潮流計算に用いる電力方程式」の通り,非零要素が極めて少ない行列をスパース行列(疎行列)といいます。
(2)解答:ニ
題意より解答候補は,(ニ)スラック,(ヘ)オイラー,(チ)補充,(リ)フラット,(カ)慣性,等になると思います。
ワンポイント解説「1.潮流計算に用いる電力方程式」の通り,電圧位相角の基準とし,系統の有効・無効電力損失分を充当させているノードをスラックノードといいます。
(3)解答:ワ
題意より解答候補は,(イ)立体,(ヌ)三角,(ワ)直角,等になると思います。
電力方程式の座標は,電圧座標の取り方に応じて直角(直交)座標又は極座標が使用されます。
(4)解答:ヨ
題意より解答候補は,(ハ)ルンゲクッタ,(ル)インピーダンス,(ヲ)加速係数,(ヨ)ニュートンラフソン,等になると思います。
ワンポイント解説「2.ニュートンラプソン法」の通り,電力方程式を解くために未知数に適当な初期値を設定して,反復計算により正解に収束させていく計算手法をニュートンラプソン法といいます。
(5)解答:ト
題意より解答候補は,(ホ)逐次係数,(ト)ヤコビアン行例,(ヲ)加速係数,等になると思います。
ワンポイント解説「2.ニュートンラプソン法」の通り,収束計算に使用する電力方程式の微分係数はヤコビアン行列と呼ばれます。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん