【問題】
【難易度】★☆☆☆☆(易しい)
次の文章は,三相交流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
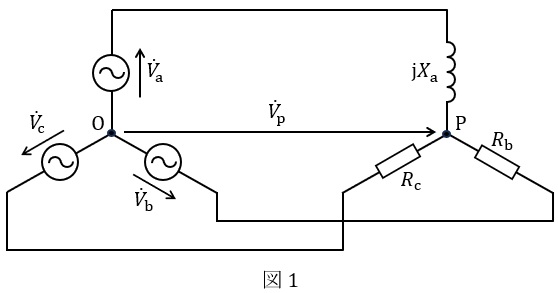
図1の回路は,\( \ \mathrm {Y} \ \)結線の対称三相電源に\( \ \mathrm {Y} \ \)結線の不平衡三相負荷が接続された不平衡三相回路である。不平衡負荷は,一つの誘導性負荷及び二つの等しい純抵抗負荷(電灯)から構成されている。ただし,誘導性負荷のリアクタンスは\( \ X_{\mathrm {a}} \ \),抵抗負荷の抵抗値は\( \ R_{\mathrm {b}} \ \),\( \ R_{\mathrm {c}} \ \)であり,\( \ X_{\mathrm {a}}=R_{\mathrm {b}}=R_{\mathrm {c}}=R \ \)とする。
ここで,対称三相電源の相回転の順が\( \ {\dot V}_{\mathrm {a}} \ → \ {\dot V}_{\mathrm {b}} \ → \ {\dot V}_{\mathrm {c}} \ \)であるとき,以下の手順に従って,対称三相電源の相回転の順(相順)と電灯の明暗の関係を考察する。
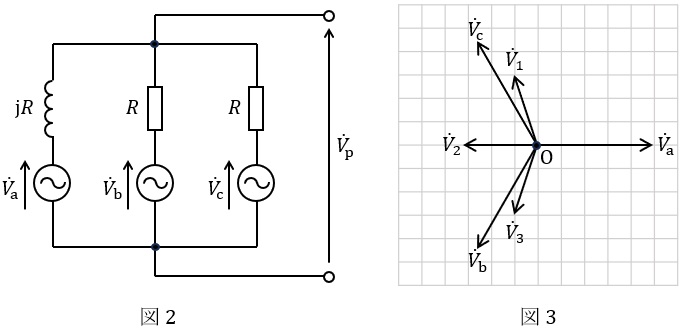
図1の不平衡三相回路は,図2に示す等価回路に変換できる。ミルマンの定理より,図2の等価回路における中性点\( \ \mathrm {O}-\mathrm {P} \ \)間の電圧\( \ {\dot V}_{\mathrm {p}} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {p}} &=&\frac {\displaystyle \frac {{\dot V}_{\mathrm {a}}}{\mathrm {j}R}+\frac {{\dot V}_{\mathrm {b}}}{R}+\frac {{\dot V}_{\mathrm {c}}}{R}}{\displaystyle \frac {1}{\mathrm {j}R}+\frac {1}{R}+\frac {1}{R}}= \ \fbox { (1) } \ ・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで対称三相電源であることから,\( \ {\dot V}_{\mathrm {b}} +{\dot V}_{\mathrm {c}}=-{\dot V}_{\mathrm {a}} \ \)の関係が成り立つので,①式の\( \ {\dot V}_{\mathrm {p}} \ \)は,\( \ {\dot V}_{\mathrm {a}} \ \)を用いて,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {p}} &=& \ \fbox { (2) } ・・・・・・・・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
と表すことができる。
図3は,相回転の順が\( \ {\dot V}_{\mathrm {a}} \ → \ {\dot V}_{\mathrm {b}} \ → \ {\dot V}_{\mathrm {c}} \ \)である対称三相電源のベクトル図を示したものであり,②式の\( \ {\dot V}_{\mathrm {p}} \ \)を表すベクトルは図3の\( \ \fbox { (3) } \ \)である。
ここで,\( \ X_{\mathrm {a}}=R_{\mathrm {b}}=R_{\mathrm {c}}=R \ \)であることに注意すれば,二つの電灯に流れる電流の大きさは\( \ \left| {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {p}} \right| \ \)と\( \ \left| {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {p}} \right| \ \)に比例する。また,図3のベクトル図より,\( \ \left| {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {p}} \right| \ \)と\( \ \left| {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {p}} \right| \ \)の間には,\( \ \fbox { (4) } \ \)の関係が成立する。したがって,二つの電灯\( \ R_{\mathrm {b}} \ \)と\( \ R_{\mathrm {c}} \ \)の明るさの関係は,\( \ \fbox { (5) } \ \)。
〔問5の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {\mathrm {j}{\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}}{2-\mathrm {j}} &(ロ)& \left| {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {p}} \right| > \left| {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {p}} \right| &(ハ)& {\dot V}_{\mathrm {2}} \\[ 5pt ]
&(ニ)& \left| {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {p}} \right| < \left| {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {p}} \right| &(ホ)& \frac {-\mathrm {j}{\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}}{2-\mathrm {j}} &(ヘ)& -\frac {1-\mathrm {j}3}{5}{\dot V}_{\mathrm {a}} \\[ 5pt ]
&(ト)& {\dot V}_{\mathrm {3}} &(チ)& -\frac {1+\mathrm {j}3}{5}{\dot V}_{\mathrm {a}} &(リ)& \left| {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {p}} \right| = \left| {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {p}} \right| \\[ 5pt ]
&(ヌ)& \frac {1+\mathrm {j}3}{5}{\dot V}_{\mathrm {a}} &(ル)& \frac {-\mathrm {j}{\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}}{2+\mathrm {j}} &(ヲ)& {\dot V}_{\mathrm {1}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
&(ワ)& 電灯 \ R_{\mathrm {b}} \ が電灯 \ R_{\mathrm {c}} \ よりも明るくなる \\[ 5pt ]
&(カ)& 電灯 \ R_{\mathrm {b}} \ が電灯 \ R_{\mathrm {c}} \ よりも暗くなる \\[ 5pt ]
&(ヨ)& 電灯 \ R_{\mathrm {b}} \ と電灯 \ R_{\mathrm {c}} \ は同じ明るさになる \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
抵抗とリアクトルの不平衡三相負荷が接続された三相回路に関する問題です。
例年難易度が高い問題が出題されやすい問5としては非常に易しい問題なので,多くの受験生が完答できた問題かと思います。
特別な公式もなく配点も高いので,ミスに注意して完答を目指すようにして下さい。
【解答】
(1)解答:ホ
①式を整理すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {p}} &=&\frac {\displaystyle \frac {{\dot V}_{\mathrm {a}}}{\mathrm {j}R}+\frac {{\dot V}_{\mathrm {b}}}{R}+\frac {{\dot V}_{\mathrm {c}}}{R}}{\displaystyle \frac {1}{\mathrm {j}R}+\frac {1}{R}+\frac {1}{R}} \\[ 5pt ]
&=&\frac {\displaystyle \frac {{\dot V}_{\mathrm {a}}}{\mathrm {j}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}}{\displaystyle \frac {1}{\mathrm {j}}+1+1} \\[ 5pt ]
&=&\frac {\displaystyle -\mathrm {j}{\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}}{2-\mathrm {j}} \left( ∵\frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j} \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:チ
(1)解答式に\( \ {\dot V}_{\mathrm {b}} +{\dot V}_{\mathrm {c}}=-{\dot V}_{\mathrm {a}} \ \)を代入して整理すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {p}} &=&\frac {\displaystyle -\mathrm {j}{\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}}{2-\mathrm {j}} \\[ 5pt ]
&=&\frac {\displaystyle -\mathrm {j}{\dot V}_{\mathrm {a}}-{\dot V}_{\mathrm {a}}}{2-\mathrm {j}} \\[ 5pt ]
&=&-\frac {\displaystyle 1+\mathrm {j}}{2-\mathrm {j}}{\dot V}_{\mathrm {a}} \\[ 5pt ]
&=&-\frac {\displaystyle 1+\mathrm {j}}{2-\mathrm {j}}\times \frac {2+\mathrm {j}}{2+\mathrm {j}}{\dot V}_{\mathrm {a}} \\[ 5pt ]
&=&-\frac {\displaystyle 2+\mathrm {j}+\mathrm {j}2-1}{4-\left( -1\right) }{\dot V}_{\mathrm {a}} \\[ 5pt ]
&=&-\frac {1+\mathrm {j}3}{5}{\dot V}_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
(2)解答式を整理すると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {p}} &=&-\frac {1+\mathrm {j}3}{5}{\dot V}_{\mathrm {a}} \\[ 5pt ]
&=&\left( -\frac {1}{5}-\mathrm {j}\frac {3}{5}\right) {\dot V}_{\mathrm {a}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,図3で\( \ {\dot V}_{\mathrm {p}} \ \)を表すベクトルは\( \ {\dot V}_{\mathrm {3}} \ \)と求められる。
(4)解答:ニ
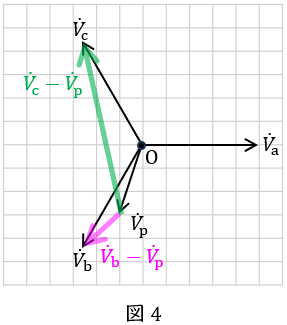
\( \ {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {p}} \ \)と\( \ {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {p}} \ \)を作図すると図4のようになる。
図4より,\( \ \left| {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {p}} \right| < \left| {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {p}} \right| \ \)であることがわかる。
(5)解答:カ
(4)解答式の通り,\( \ R_{\mathrm {b}} \ \)に加わる電圧\( \ \left| {\dot V}_{\mathrm {b}}-{\dot V}_{\mathrm {p}} \right| \ \)は\( \ R_{\mathrm {c}} \ \)に加わる電圧\( \ \left| {\dot V}_{\mathrm {c}}-{\dot V}_{\mathrm {p}} \right| \ \)より小さく,電流値も小さくなるので,電灯\( \ R_{\mathrm {b}} \ \)が電灯\( \ R_{\mathrm {c}} \ \)よりも暗くなることがわかる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん