【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は図を解答群の中から選び,その記号をマークシートに記入しなさい。
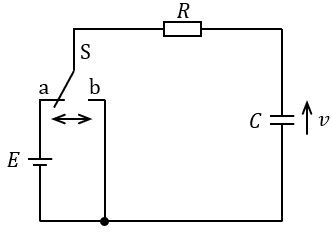
図のように,抵抗\( \ R \ \),静電容量\( \ C \ \)及び電圧源\( \ E \ \)を接続した回路がある。この回路における静電容量\( \ C \ \)の両端の電圧\( \ v \ \)の時間的変化を求めたい。
スイッチ\( \ \mathrm {S} \ \)は静電容量\( \ C \ \)の両端の電圧\( \ v \ \)によって次のように制御される。
\[
\begin{eqnarray}
\left\{
\begin{array}{l}
v=V_{1} \ のとき,\ \mathrm {b} \ 側から \ \mathrm {a} \ 側に切り替わる。 \\[ 5pt ]
v=V_{2} \ のとき,\ \mathrm {a} \ 側から \ \mathrm {b} \ 側に切り替わる。 \\[ 5pt ]
ここで,V_{1} \lt V_{2} \lt E \ とする。 \\[ 5pt ]
\end{array}
\right\}
\end{eqnarray}
\]
時刻\( \ t = 0 \ \)では,スイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {a} \ \)側にあり,\( \ v \ \)の初期値は\( \ V_{1} \ \)である。
時刻\( \ t \gt 0 \ \)において,スイッチが切り替わる時刻を順に\( \ T_{1} \ \),\( \ T_{2} \ \),\( \ \cdots \ \)とする。
\( \ 0≦t \lt T_{1} \ \)における\( \ v \ \)の時間的変化は次式で表される。
\[
\begin{eqnarray}
v &=& \ \fbox { (1) } \ \ ・・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
\( \ v=V_{2} \ \)となった瞬間,スイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {a} \ \)側から\( \ \mathrm {b} \ \)側に切り替わる。この時刻\( \ T_{1} \ \)は次式で表される。
\[
\begin{eqnarray}
T_{1} &=& \ \fbox { (2) } ・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
\( \ T_{1}≦t \lt T_{2} \ \)における\( \ v \ \)の時間的変化は次式で表される。
\[
\begin{eqnarray}
v &=& \ \fbox { (3) } \ \ ・・・・・・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
\( \ v=V_{1} \ \)となった瞬間,スイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {b} \ \)側から\( \ \mathrm {a} \ \)側に切り替わる。この時刻\( \ T_{2} \ \)は,
\[
\begin{eqnarray}
T_{2} &=&T_{1}+ \ \fbox { (4) } \ ・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
である。
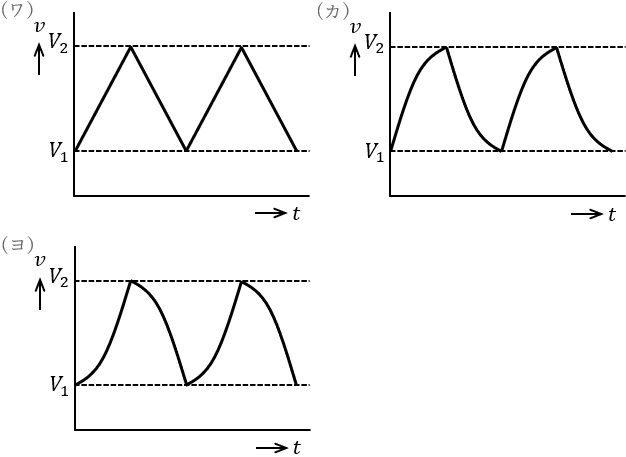
\( \ v \ \)はスイッチにより,\( \ V_{1} \ \)と\( \ V_{2} \ \)の間で上昇・下降を繰り返す。この様子を示す\( \ v \ \)の波形は\( \ \fbox { (5) } \ \)である。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& CR\log _{e}\frac {E-V_{1}}{E-V_{2}} &(ロ)& CR\log _{e}\frac {V_{1}}{V_{2}-V_{1}} &(ハ)& V_{2}\left( 1-e^{-\frac {1}{CR}\left( t-T_{1}\right) }\right) \\[ 5pt ]
&(ニ)& CR\log _{e}\frac {E}{V_{2}-V_{1}} &(ホ)& Ee^{-\frac {1}{CR}t}+V_{1} &(ヘ)& V_{2}-Ee^{-\frac {1}{CR}\left( t-T_{1}\right) } \\[ 5pt ]
&(ト)& V_{2} e^{-\frac {1}{CR}\left( t-T_{1}\right) } &(チ)& CR\log _{e}\frac {V_{2}}{V_{1}} &(リ)& E\left( 1-e^{-\frac {1}{CR}t}\right) +V_{1} \\[ 5pt ]
&(ヌ)& \left( V_{1}-E\right) e^{-\frac {1}{CR}t}+E \ &(ル)& CR\log _{e}\frac {V_{2}}{V_{2}-V_{1}} &(ヲ)& CR\log _{e}\frac {E}{E-V_{2}+V_{1}} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
スイッチ切換えを伴う\( \ RC \ \)直列回路の過渡現象に関する問題です。
スイッチ切換え以外は一般的な\( \ RC \ \)直列回路の基本回路となります。初期条件だけ注意して完答を目指すようにしましょう。
1.過渡現象における\( \ RLC \ \)それぞれの電圧
線路に流れる電流を\( \ i \ \mathrm {[A]} \ \)とし,抵抗\( \ R \ \mathrm {[\Omega ]} \ \)の電圧\( \ V_{\mathrm{R}} \ \mathrm {[V]} \ \),リアクトル\( \ L \ \mathrm {[H]} \ \)の電圧\( \ V_{\mathrm{L}} \ \mathrm {[V]} \ \),コンデンサ\( \ C \ \mathrm {[F]} \ \)の電圧\( \ V_{\mathrm{C}} \ \mathrm {[V]} \ \)とすると,
\[
\begin{eqnarray}
V_{\mathrm{R}} &=& Ri \\[ 5pt ]
V_{\mathrm{L}} &=& L\frac {\mathrm {d}i}{\mathrm {d}t} \\[ 5pt ]
V_{\mathrm{C}} &=& \frac {1}{C}\int i \mathrm {d}t =\frac {q}{C}\\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ i=i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \left ( \ln {x} \right) &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} \mathrm {d}x&=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時, x=A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right)となります。 \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ヌ
コンデンサに蓄えられる電荷を\( \ q \ \)とする。\( \ 0≦t \lt T_{1} \ \)のとき,スイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {a} \ \)側なので,回路方程式は,ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電圧」の通り,
\[
\begin{eqnarray}
Ri+\frac {q}{C}&=&E \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ \displaystyle i=\frac {\mathrm {d}q}{\mathrm {d}t} \ \)であるから,
\[
\begin{eqnarray}
R\frac {\mathrm {d}q}{\mathrm {d}t}+\frac {q}{C}&=&E \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで過渡解を\( \ q_{t} \ \)とすれば,
\[
\begin{eqnarray}
R\frac {\mathrm {d}q_{t}}{\mathrm {d}t}+\frac {q_{t}}{C}&=&0 \\[ 5pt ]
R\frac {\mathrm {d}q_{t}}{\mathrm {d}t}&=&-\frac {q_{t}}{C} \\[ 5pt ]
\frac {1}{q_{t}}\mathrm {d}q_{t}&=&-\frac {1}{RC}\mathrm {d}t \\[ 5pt ]
\int \frac {1}{q_{t}}\mathrm {d}q_{t}&=&\int -\frac {1}{RC}\mathrm {d}t \\[ 5pt ]
\ln q_{t}&=&-\frac {1}{RC}t+C \left( C \ は積分定数\right) \\[ 5pt ]
q_{t}&=&Ae^{-\frac {1}{RC}t} \left( A \ は積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,定常解を\( \ q_{s} \ \)とすれば,\( \ \displaystyle \frac {\mathrm {d}q}{\mathrm {d}t}=0 \ \)なので,
\[
\begin{eqnarray}
\frac {q_{s}}{C}&=&E \\[ 5pt ]
q_{s}&=&CE \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,一般解は,
\[
\begin{eqnarray}
q&=&q_{s}+q_{t} \\[ 5pt ]
&=&CE+Ae^{-\frac {1}{RC}t} \\[ 5pt ]
\end{eqnarray}
\]
となる。時刻\( \ t=0 \ \)のとき,初期条件\( \ q (0)=CV_{1} \ \)なので,
\[
\begin{eqnarray}
CV_{1}&=&CE+Ae^{-\frac {1}{RC}\times 0} \\[ 5pt ]
CV_{1}&=&CE+A \\[ 5pt ]
A&=&CV_{1}-CE \\[ 5pt ]
&=&C\left( V_{1}-E\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
q&=&CE+C\left( V_{1}-E\right) e^{-\frac {1}{RC}t} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,コンデンサ電圧\( \ v \ \)は,
\[
\begin{eqnarray}
v&=&\frac {q}{C} \\[ 5pt ]
&=&\frac {CE+C\left( V_{1}-E\right) e^{-\frac {1}{RC}t}}{C} \\[ 5pt ]
&=&E+\left( V_{1}-E\right) e^{-\frac {1}{RC}t} \\[ 5pt ]
&=&\left( V_{1}-E\right) e^{-\frac {1}{CR}t}+E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:イ
(1)解答式より,\( \ v=V_{2} \ \)となる時刻\( \ T_{1} \ \)は,
\[
\begin{eqnarray}
V_{2}&=&\left( V_{1}-E\right) e^{-\frac {1}{CR}T_{1}}+E \\[ 5pt ]
V_{2}-E&=&\left( V_{1}-E\right) e^{-\frac {1}{CR}T_{1}} \\[ 5pt ]
e^{-\frac {1}{CR}T_{1}}&=&\frac {V_{2}-E}{V_{1}-E} \\[ 5pt ]
e^{\frac {1}{CR}T_{1}}&=&\frac {V_{1}-E}{V_{2}-E} \\[ 5pt ]
\frac {1}{CR}T_{1}&=&\log _{e} \frac {V_{1}-E}{V_{2}-E} \\[ 5pt ]
T_{1}&=&CR\log _{e}\frac {V_{1}-E}{V_{2}-E} \\[ 5pt ]
&=&CR\log _{e}\frac {E-V_{1}}{E-V_{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ト
(1)と同様に,スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {b} \ \)側に切り替わった後の\( \ q \ \)の一般解は,
\[
\begin{eqnarray}
q&=&Ae^{-\frac {1}{RC}t} \left( A \ は積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,時刻\( \ T_{1} \ \)のとき,\( \ q (T_{1})=CV_{2} \ \)なので,
\[
\begin{eqnarray}
CV_{2}&=&Ae^{-\frac {1}{RC}T_{1}} \\[ 5pt ]
A&=&CV_{2}e^{\frac {1}{RC}T_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
q&=&CV_{2}e^{\frac {1}{RC}T_{1}}e^{-\frac {1}{RC}t} \\[ 5pt ]
&=&CV_{2}e^{-\frac {1}{RC}(t-T_{1}) } \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,コンデンサ電圧\( \ v \ \)は,
\[
\begin{eqnarray}
v&=&\frac {q}{C} \\[ 5pt ]
&=&\frac {CV_{2}e^{-\frac {1}{RC}(t-T_{1}) }}{C} \\[ 5pt ]
&=&V_{2}e^{-\frac {1}{CR}(t-T_{1}) } \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:チ
(3)解答式より,\( \ v=V_{1} \ \)となる時刻\( \ T_{2} \ \)は,
\[
\begin{eqnarray}
V_{1}&=&V_{2}e^{-\frac {1}{CR}(T_{2}-T_{1}) } \\[ 5pt ]
e^{-\frac {1}{CR}(T_{2}-T_{1}) }&=&\frac {V_{1}}{V_{2}} \\[ 5pt ]
e^{\frac {1}{CR}(T_{2}-T_{1}) }&=&\frac {V_{2}}{V_{1}} \\[ 5pt ]
\frac {1}{CR}(T_{2}-T_{1}) &=&\log _{e}\frac {V_{2}}{V_{1}} \\[ 5pt ]
T_{2}-T_{1}&=&CR\log _{e}\frac {V_{2}}{V_{1}} \\[ 5pt ]
T_{2}&=&T_{1}+CR\log _{e}\frac {V_{2}}{V_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:カ
(2),(4)解答式より,グラフとして適当なのは(カ)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん