【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,回路の過渡現象に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
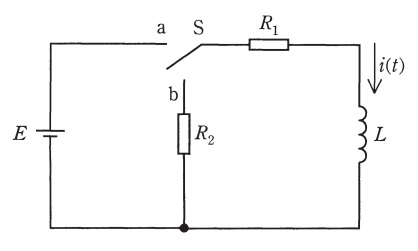
図の回路において,時刻\( \ t < 0 \ \)では,スイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {a} \ \)側にあり,回路は定常状態にあるものとする。
時刻\( \ t = 0 \ \)で,スイッチ\( \ \mathrm {S} \ \)を\( \ \mathrm {b} \ \)側に切り換えたとする。時刻\( \ t ≧ 0 \ \)において,キルヒホッフの電圧則に従う微分方程式が成立するが,この微分方程式の両辺をラプラス変換し,コイル\( \ L \ \)を流れる電流\( \ I ( s ) =\mathcal{L} \left[ i(t)\right] \ \)を求めると,
\[
\begin{eqnarray}
I(s)&=&\fbox { (1) }i(0) ・・・・・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ i(0) \ \)は時刻\( \ t=0 \ \)におけるコイルの電流であり,
\[
\begin{eqnarray}
i(0)&=&\fbox { (2) } ・・・・・・・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
で与えられる。
ラプラス逆変換により,時刻\( \ t ≧ 0 \ \)における電流\( \ i(t) \ \)は,
\[
\begin{eqnarray}
i(t)&=&\mathcal{L}^{-1}[I(s)]=\fbox { (3) } ・・・・・・・・・・・・ ③ \\[ 5pt ]
\end{eqnarray}
\]
となる。
一方,\( \ t=\infty \ \)における電流\( \ i(\infty ) \ \)は,①式及び②式で求めた\( \ I(s) \ \)にラプラス変換の最終値定理を適用すれば,
\[
\begin{eqnarray}
i(\infty )&=&\fbox { (4) } ・・・・・・・・・・・・・・・・・・ ④ \\[ 5pt ]
\end{eqnarray}
\]
と表される。
また,スイッチ\( \ \mathrm {S} \ \)を\( \ \mathrm {b} \ \)側に切り換えた後に,\( \ t=\infty \ \)までに抵抗\( \ R_{1} \ \)で消費されるエネルギー\( \ W \ \)は,
\[
\begin{eqnarray}
W&=&\fbox { (5) } ・・・・・・・・・・・・・・・・・・・ ⑤ \\[ 5pt ]
\end{eqnarray}
\]
となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {E}{R_{1}+R_{2}} &(ロ)& \frac {L}{sL+R_{1}+R_{2}} &(ハ)& \displaystyle \lim_{ s \to \infty } \frac {sLE}{sR_{1}L+R_{1}(R_{1}+R_{2})} \\[ 5pt ]
&(ニ)& \frac {E}{R_{1}} &(ホ)& \frac {E}{R_{2}} &(ヘ)& \frac {E}{R_{1}+R_{2}}\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t} \\[ 5pt ]
&(ト)& \frac {L}{sL+R_{2}} &(チ)& \frac {L}{sL+R_{1}} &(リ)& \displaystyle \lim_{ s \to 0 } \frac {sLE}{sR_{1}L+R_{1}(R_{1}+R_{2})} \\[ 5pt ]
&(ヌ)& \frac {E}{R_{2}}\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t} &(ル)& \frac {E^{2}}{2(R_{1}+R_{2})} &(ヲ)& \displaystyle \lim_{ s \to \infty } \frac {LE}{s^{2}R_{1}L+sR_{1}(R_{1}+R_{2})} \\[ 5pt ]
&(ワ)& \frac {LE^{2}}{2R_{1}(R_{1}+R_{2})} &(カ)& \frac {E}{R_{1}}\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t} &(ヨ)& \frac {LE^{2}}{2R_{2}(R_{1}+R_{2})}
\end{eqnarray}
\]
【ワンポイント解説】
ラプラス変換は二種の二次試験でもよく出題されていたと思います。下記に示すラプラス変換と最終値の定理はよく出題されます。必ず暗記しておいて下さい。
1.代表的なラプラス変換とラプラス逆変換
\(f(t)\)のラプラス変換\(F(s)\)とすると,最低限以下の変換を覚えておく必要があります。
\[
\begin{eqnarray}
&①& f(t)=K(定数) &⇔& F(s)=\frac {K}{s} \\[ 5pt ]
&②& f(t)=t &⇔& F(s)=\frac {1}{s^{2}} \\[ 5pt ]
&③& f(t)=\mathrm {e}^{at} &⇔& F(s)=\frac {1}{s-a} \\[ 5pt ]
&④& f(t)=\cos \omega t &⇔& F(s)=\frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
&⑤& f(t)=\sin \omega t &⇔& F(s)=\frac {\omega }{s^{2}+\omega ^{2}}
\end{eqnarray}
\]
2.微分と積分のラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,
\[
\begin{eqnarray}
\mathcal{L}[f^{\prime }(t)]&=&sF(s)-f(0) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\mathcal{L}\left[ \int ^{t}_{0}f(\tau )\mathrm {d}\tau \right] &=&\frac {1}{s}F(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.最終値の定理
時間関数\( \ f(t) \ \)とそのラプラス変換\( \ F(s) \ \)が与えられている時,
\[
\begin{eqnarray}
\displaystyle \lim_{ t \to \infty }f(t) &=&\lim_{ s \to 0 }sF(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)解答:ロ
スイッチ\( \ \mathrm {S} \ \)を\( \ \mathrm {b} \ \)側に切り換えた後の回路方程式は,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i(t)}{\mathrm {d}t}+(R_{1}+R_{2})i(t)&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。上式をラプラス変換すると,
\[
\begin{eqnarray}
L\left\{ sI(s)-i(0)\right\}+(R_{1}+R_{2}) I(s)&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ I(s) \ \)について整理すると,
\[
\begin{eqnarray}
sLI(s)-Li(0)+(R_{1}+R_{2})I(s) &=& 0 \\[ 5pt ]
(sL+R_{1}+R_{2})I(s) &=& Li(0) \\[ 5pt ]
I(s) &=& \frac {L}{sL+R_{1}+R_{2}}i(0) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ニ
\( \ t \lt 0 \ \)において,スイッチ\( \ \mathrm {S} \ \)は\( \ \mathrm {a} \ \)側にあり,回路は定常状態であるから,コイル\( \ L \ \)の電圧降下はないので,
\[
\begin{eqnarray}
R_{1}i\left( 0\right) &=&E \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,
\[
\begin{eqnarray}
i\left( 0\right) &=&\frac {E}{R_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となる。
(3)解答:カ
(1),(2)より\( \ I(s) \ \)は,
\[
\begin{eqnarray}
I(s)&=&\frac {L}{sL+R_{1}+R_{2}}\frac {E}{R_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となるから,\( \ I(s) \ \)を逆ラプラス変換すると,
\[
\begin{eqnarray}
i(t) &=& \mathcal{L}^{-1}[I(s)] \\[ 5pt ]
&=& \frac {E}{R_{1}}\mathcal{L}^{-1}\left[ \frac {1}{s+\frac {R_{1}+R_{2}}{L}}\right] \\[ 5pt ]
&=& \frac {E}{R_{1}}\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t}
\end{eqnarray}
\]
と求められる。
(4)解答:リ
最終値の定理より,
\[
\begin{eqnarray}
\displaystyle \lim_{ t \to \infty }i(t) &=& \lim_{ s \to 0 }sI(s) \\[ 5pt ]
&=& \lim_{ s \to 0 }s\frac {L}{sL+R_{1}+R_{2}}\frac {E}{R_{1}} \\[ 5pt ]
&=& \displaystyle \lim_{ s \to 0 } \frac {sLE}{sR_{1}L+R_{1}(R_{1}+R_{2})}
\end{eqnarray}
\]
となる。
(5)解答:ワ
スイッチ\( \ \mathrm {S} \ \)を\( \ \mathrm {b} \ \)側に切り換えた後に,\( \ t=\infty \ \)までに抵抗\( \ R_{1} \ \)で消費されるエネルギー\( \ W \ \)は,
\[
\begin{eqnarray}
W &=& \int ^{\infty }_{0}R_{1}i(t)^{2}\mathrm {d}t \\[ 5pt ]
&=& \int ^{\infty }_{0}R_{1}\left( \frac {E}{R_{1}}\mathrm {e}^{-\frac {R_{1}+R_{2}}{L}t}\right) ^{2}\mathrm {d}t \\[ 5pt ]
&=& \frac {E^{2}}{R_{1}}\int ^{\infty }_{0}\mathrm {e}^{-\frac {2(R_{1}+R_{2})}{L}t} \mathrm {d}t \\[ 5pt ]
&=& \frac {E^{2}}{R_{1}}\left[ -\frac {L}{2(R_{1}+R_{2})}\mathrm {e}^{-\frac {2(R_{1}+R_{2})}{L}t}\right] ^{\infty }_{0} \\[ 5pt ]
&=& \frac {LE^{2}}{2R_{1}(R_{1}+R_{2})}
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん