【問題】
【難易度】★★★☆☆(普通)
次の文章は,線電荷周囲の電界に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。ただし,空間の誘電率は\( \ \varepsilon _{0} \ \)とし,各図は断面図である。
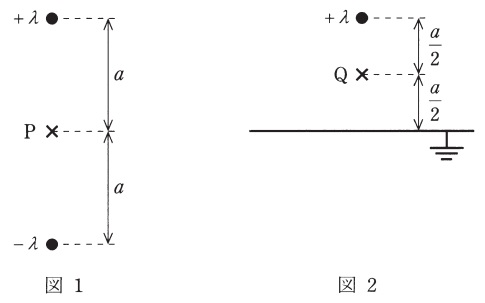
図1のように,線電荷密度の大きさが\( \ \lambda \ \)であり,極性が異なる\( \ 2 \ \)本の無限長線電荷が互いに平行に距離\( \ 2a \ \)を隔てて置かれている場合,中間点\( \ \mathrm {P} \ \)での電界の大きさは\( \ \fbox { (1) } \ \)である。またこのとき,線電荷に生じる単位長さ当たりの力の大きさは\( \ \fbox { (2) } \ \)となる。
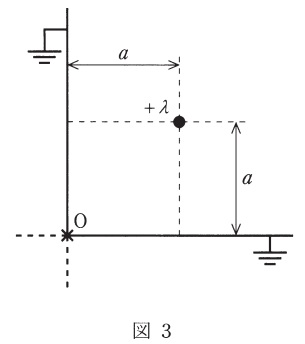
次に,図2のように,線電荷密度が\( \ \lambda \ \)である無限長線電荷が,接地平面と平行に距離\( \ a \ \)を隔てて置かれている場合を考える。このとき,電界の境界条件より,接地面には電気力線が面に垂直に入射することに留意して,影像線電荷を考えると,線電荷と接地面との中間点\( \ Q \ \)での電界の大きさは\( \ \fbox { (3) } \ \)と求めることができる。
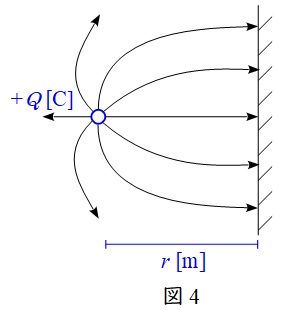
さらに,図3のように直交する\( \ 2 \ \)枚の接地平面があり,両平面と平行に距離\( \ a \ \)を隔てて,線電荷密度が\( \ \lambda \ \)である無限長線電荷が置かれている。この場合,電界の境界条件を考えると,点\( \ \mathrm {O} \ \)における電界の大きさは\( \ \fbox { (4) } \ \)になる。この場合の境界条件を満たす影像線電荷を考えると,線電荷に生じる単位長さ当たりの力の大きさは\( \ \fbox { (5) } \ \)と求めることができる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {2\lambda }{3\pi \varepsilon _{0}a} &(ロ)& \frac {\lambda }{\pi \varepsilon _{0}a} &(ハ)& \frac {3\lambda }{4\pi \varepsilon _{0}a} \\[ 5pt ]
&(ニ)& \frac {\sqrt {2}\lambda ^{2} }{8\pi \varepsilon _{0}a} &(ホ)& \frac {\sqrt {2}\lambda ^{2} }{4\pi \varepsilon _{0}a} &(ヘ)& \frac {\sqrt {2}\lambda }{2\pi \varepsilon _{0}a} \\[ 5pt ]
&(ト)& \frac {\lambda ^{2} }{2\pi \varepsilon _{0}a} &(チ)& \frac {\sqrt {2}\lambda ^{2} }{2\pi \varepsilon _{0}a} &(リ)& \frac {4\lambda }{3\pi \varepsilon _{0}a} \\[ 5pt ]
&(ヌ)& \frac {\lambda }{4\pi \varepsilon _{0}a} &(ル)& \frac {\lambda ^{2} }{8\pi \varepsilon _{0}a} &(ヲ)& 0 \\[ 5pt ]
&(ワ)& \frac {\sqrt {2}\lambda }{4\pi \varepsilon _{0}a} &(カ)& \frac {\lambda ^{2} }{4\pi \varepsilon _{0}a} &(ヨ)& \frac {\lambda }{2\pi \varepsilon _{0}a} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
無限線電荷により発生する周囲の電界や力の大きさの導出に関する問題です。
解法は一般的な点電荷とあまり変わりませんが,点電荷より参考書での取り扱いも少ないと思うので,本問を通じて違いを理解しておくようにしましょう。
1.ガウスの法則
誘電率\( \ \varepsilon \ \mathrm {[F/m]} \ \)の空間において,\( \ Q \ [ \mathrm {C} ] \ \)から出る電気力線は\( \ \displaystyle \frac {Q}{\varepsilon } \ \)本であり,電界\( \ E \ \mathrm {[V/m]} \ \)との関係は,任意の閉曲面において,
\[
\begin{eqnarray}
\int _{S} \boldsymbol E \cdot \mathrm {d}\boldsymbol S &=& \frac {Q}{\varepsilon } \\[ 5pt ]
\end{eqnarray}
\]
となります。閉局面が同軸円筒導体であれば,線電荷密度を\( \ \lambda \ [ \mathrm {C/m} ] \ \)とすると,単位長さ当たりの電界\( \ E \ \mathrm {[V/m]} \ \)は,
\[
\begin{eqnarray}
2\pi r E &=& \frac {\lambda }{\varepsilon } \\[ 5pt ]
E &=& \frac {\lambda }{2\pi \varepsilon r} \\[ 5pt ]
\end{eqnarray}
\]
となります。
2.電気影像法
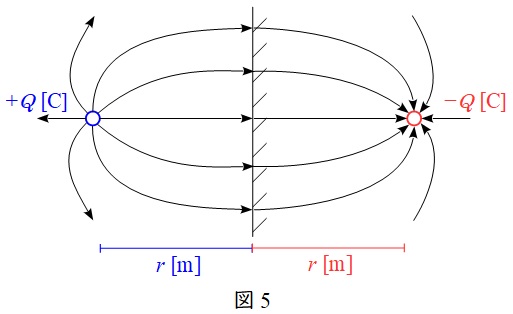
図4のような平面導体から距離\( \ r \ \)を隔てて電荷があるとき,電気力線は導体に垂直に入射するため,図5のように符号が逆の電荷(仮想電荷)を設定して電界を求めることができます。これを電気影像法といいます。
【関連する「電気の神髄」記事】
【解答】
(1)解答:ロ
ワンポイント解説「1.ガウスの法則」の通り,単位長さ当たりの線電荷\( \ +\lambda \ \)が距離\( \ a \ \)離れた点\( \ \mathrm {P} \ \)に作る電界の大きさ\( \ E_{\mathrm {P}1} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {P}1} &=& \frac {\lambda }{2\pi \varepsilon _{0}a} (下向き) \\[ 5pt ]
\end{eqnarray}
\]
であり,単位長さ当たりの線電荷\( \ -\lambda \ \)が距離\( \ a \ \)離れた点\( \ \mathrm {P} \ \)に作る電界の大きさ\( \ E_{\mathrm {P}2} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {P}2} &=& \frac {\lambda }{2\pi \varepsilon _{0}a}(下向き)\\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ E_{\mathrm {P}1} \ \)と\( \ E_{\mathrm {P}2} \ \)は同じ向きとなるので,点\( \ \mathrm {P} \ \)の電界の大きさ\( \ E_{\mathrm {P}} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {P}} &=& E_{\mathrm {P}1}+E_{\mathrm {P}2} \\[ 5pt ]
&=& \frac {\lambda }{2\pi \varepsilon _{0}a}+\frac {\lambda }{2\pi \varepsilon _{0}a} \\[ 5pt ]
&=& \frac {\lambda }{\pi \varepsilon _{0}a} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:カ
単位長さ当たりの線電荷\( \ +\lambda \ \)が距離\( \ 2a \ \)離れた点に作る電界の大きさ\( \ E_{-\lambda} \ \)は,
\[
\begin{eqnarray}
E_{-\lambda} &=& \frac {\lambda }{2\pi \varepsilon _{0}\cdot 2a} \\[ 5pt ]
&=& \frac {\lambda }{4\pi \varepsilon _{0}a} (下向き) \\[ 5pt ]
\end{eqnarray}
\]
となるので,単位長さ当たりの線電荷\( \ -\lambda \ \)にかかる力の大きさ\( \ F_{\mathrm {P}} \ \)は,
\[
\begin{eqnarray}
F_{\mathrm {P}} &=& \lambda E_{-\lambda } \\[ 5pt ]
&=& \lambda \cdot \frac {\lambda }{4\pi \varepsilon _{0} a} \\[ 5pt ]
&=& \frac {\lambda ^{2} }{4\pi \varepsilon _{0}a} (上向き) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
ワンポイント解説「2.電気影像法」の通り,図2の場合における\( \ \mathrm {Q} \ \)の電界\( \ E_{\mathrm {Q}} \ \)は,反対の極性の電荷\( \ -\lambda \ \)を導体から距離\( \ a \ \)を隔てて反対側に設定すれば良いので,(1)と同様に,
\[
\begin{eqnarray}
E_{\mathrm {Q}} &=& \frac {\lambda }{\displaystyle 2\pi \varepsilon _{0}\cdot \frac {a}{2}}+\frac {\lambda }{\displaystyle 2\pi \varepsilon _{0}\cdot \frac {3a}{2}} \\[ 5pt ]
&=& \frac {\lambda }{\displaystyle \pi \varepsilon _{0}a}+\frac {\lambda }{\displaystyle 3\pi \varepsilon _{0}a} \\[ 5pt ]
&=& \frac {4\lambda }{3\pi \varepsilon _{0}a} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヲ
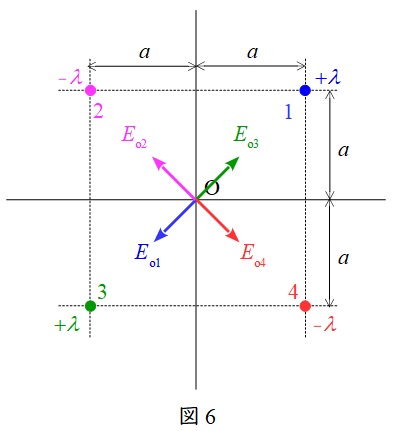
ワンポイント解説「2.電気影像法」に沿って図3の図を書き換えると図6のようになる。
ここで,図6に示すように各線電荷を\( \ 1 \ \),\( \ 2 \ \),\( \ 3 \ \),\( \ 4 \ \)とする。それぞれが点\( \ \mathrm {O} \ \)に作る電界の大きさを\( \ E_{\mathrm {O1}} \ \),\( \ E_{\mathrm {O2}} \ \),\( \ E_{\mathrm {O3}} \ \),\( \ E_{\mathrm {O4}} \ \)とすると,各電荷の向きは線電荷の符号に注意すると,図6のようになる。
それぞれの大きさは等しく,
\[
\begin{eqnarray}
E_{\mathrm {O1}}&=&E_{\mathrm {O2}}=E_{\mathrm {O3}}=E_{\mathrm {O4}} \\[ 5pt ]
&=& \frac {\lambda }{2\pi \varepsilon _{0}\cdot \sqrt {2}a} \\[ 5pt ]
&=& \frac {\lambda }{2\sqrt {2}\pi \varepsilon _{0}a} \\[ 5pt ]
\end{eqnarray}
\]
となり,合成すると,点\( \ \mathrm {O} \ \)の電界の大きさは\( \ 0 \ \)と求められる。
(5)解答:ニ
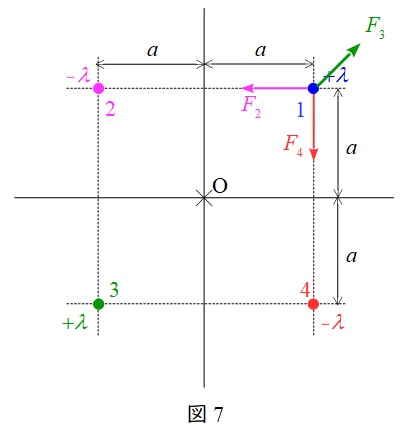
(2)より,各線電荷と\( \ 1 \ \)の線電荷にかかる力の大きさをそれぞれ\( \ F_{\mathrm {2}} \ \),\( \ F_{\mathrm {3}} \ \),\( \ F_{\mathrm {4}} \ \)とすると,図7のようになり,それぞれの力の大きさは,
\[
\begin{eqnarray}
F_{\mathrm {2}}&=&F_{\mathrm {4}} \\[ 5pt ]
&=& \frac {\lambda^{2} }{4\pi \varepsilon _{0}a} \\[ 5pt ]
F_{\mathrm {3}}&=& \frac {\lambda^{2} }{4\sqrt {2}\pi \varepsilon _{0}a} \\[ 5pt ]
&=& \frac {\sqrt {2}\lambda^{2} }{8\pi \varepsilon _{0}a} \\[ 5pt ]
\end{eqnarray}
\]
となる。
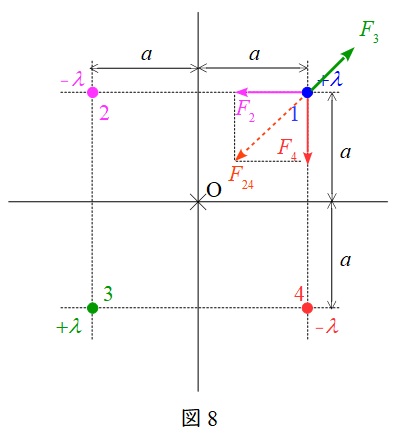
\( \ F_{\mathrm {2}} \ \),\( \ F_{\mathrm {4}} \ \)の合成力\( \ F_{\mathrm {24}} \ \)は,図8に示す通りであり,
\[
\begin{eqnarray}
F_{\mathrm {24}}&=&\sqrt {2}F_{\mathrm {2}} \\[ 5pt ]
&=&\sqrt {2}\cdot \frac {\lambda^{2} }{4\pi \varepsilon _{0}a} \\[ 5pt ]
&=& \frac {\sqrt {2}\lambda^{2} }{4\pi \varepsilon _{0}a} \\[ 5pt ]
\end{eqnarray}
\]
となるから,全体の合成力\( \ F_{\mathrm {l}} \ \)は,
\[
\begin{eqnarray}
F_{\mathrm {l}}&=&F_{\mathrm {24}}-F_{\mathrm {3}} \\[ 5pt ]
&=&\frac {\sqrt {2}\lambda^{2} }{4\pi \varepsilon _{0}a}-\frac {\sqrt {2}\lambda^{2} }{8\pi \varepsilon _{0}a} \\[ 5pt ]
&=& \frac {\sqrt {2}\lambda^{2} }{8\pi \varepsilon _{0}a} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん