《理論》〈電気及び電子計測〉[H19:問4]コンデンサ形計器用変圧器の原理に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，コンデンサ形計器用変圧器の原理に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式を解答群の中から選び，その記号をマークシートに記入しなさい。

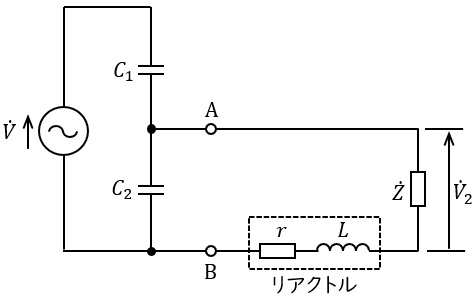
図はコンデンサ形計器用変圧器の等価回路を表したものである。図において，\( \ C_{1} \ \)及び\( \ C_{2} \ \)は静電容量，\( \ r \ \)はリアクトルの抵抗，\( \ L \ \)はリアクトルのインダクタンス，\( \ \dot Z \ \)は負荷のインピーダンスである。ただし，電源の角周波数は\( \ \omega \ \)とする。

図より，変圧比は電源電圧\( \ \dot V \ \)と負荷の電圧\( \ {\dot V}_{2} \ \)のそれぞれの大きさの比から求められる。

まず，負荷を開放して端子\( \ \mathrm {A-B} \ \)から電源側をみたインピーダンスを\( \ {\dot Z}_{0} \ \)とすると，\( \ {\dot Z}_{0}= \ \fbox {　 （１） 　} \ \)となり，また，そのときの端子\( \ \mathrm {A-B} \ \)間に現れる電圧を\( \ {\dot V}_{1} \ \)とすると，\( \ {\dot V}_{1}= \ \fbox {　 （２） 　} \ \times \dot V \ \)で表される。したがって,
\[
\begin{eqnarray}
{\dot V}_{2} &=&\frac {\dot Z}{{\dot Z}_{0}+r+j\omega L+\dot Z}\times {\dot V}_{1}= \ \fbox {　 （３） 　} \ \times \dot V \\[ 5pt ] \end{eqnarray}
\] となる。

ここで，\( \ L \ \)，\( \ C_{1} \ \)，\( \ C_{2} \ \)を適宜選んで\( \ \omega ^{2}L\left( C_{1}+C_{2} \right) =1 \ \)の条件を満足させると，\( \ {\dot V}_{2} \ \)は\( \ \fbox {　 （４） 　} \ \times \dot V \ \)となる。また，リアクトルの抵抗は負荷のインピーダンスより十分小さいと仮定して\( \ r≪\left| \dot Z \right| \ \)とすれば，変圧比\( \ k \ \)は\( \ \displaystyle k=\frac {\left| \dot V \right| }{\left| {\dot V}_{2} \right| } \ \)より\( \ \fbox {　 （５） 　} \ \)となる。このことから\( \ C_{1} \ \)及び\( \ C_{2} \ \)を適切に選ぶことにより，高電圧を適当な大きさの低電圧に変換できることが分かる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {C_{1}+C_{2}}{C_{1}}\times \frac {\dot Z}{1+r}　　　　　&（ロ）&　\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1+\frac {r}{\dot Z}+j\frac {1}{\dot Z}\left[ \omega L -\frac {1}{\omega \left( C_{1}+C_{2}\right) }\right] } \\[ 5pt ] &（ハ）&　\frac {C_{2}}{C_{1}+C_{2}}　　　　　&（ニ）&　\frac {1}{j\omega C_{1}} \\[ 5pt ] &（ホ）&　\frac {C_{1}+C_{2}}{C_{1}}　　　　　&（ヘ）&　\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1-\frac {r}{\dot Z}} \\[ 5pt ] &（ト）&　C_{2}　　　　　&（チ）&　\frac {1}{j\omega \left( C_{1}+C_{2}\right) } \\[ 5pt ] &（リ）&　j\omega \left( C_{1}+C_{2}\right) 　　　　　&（ヌ）&　\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1-\frac {r}{\dot Z}+j\frac {1}{\dot Z}\left[ \omega L +\frac {1}{\omega \left( C_{1}+C_{2}\right) }\right] } \\[ 5pt ] &（ル）&　\frac {C_{1}}{C_{1}+C_{2}}　　　　　&（ヲ）&　\frac {C_{2}}{C_{1}} \\[ 5pt ] &（ワ）&　\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1+\frac {r}{\dot Z}}　　　　　&（カ）&　\frac {C_{1}+C_{2}}{C_{1}}\times \frac {\dot Z}{\displaystyle 1+r+j\left[ \omega L -\frac {1}{\omega \left( C_{1}+C_{2}\right) }\right] } \\[ 5pt ] &（ヨ）&　\frac {C_{1}r}{C_{1}+C_{2}}　　　　　&& \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

コンデンサ形計器用変圧器の原理に関する問題です。
分野は電気及び電子計測の範囲としていますが，内容は交流回路の回路演算となります。
本問のような問題は受験生の正答率も非常に高いと予想されますので，計算間違いに注意して完答を目指すようにして下さい。

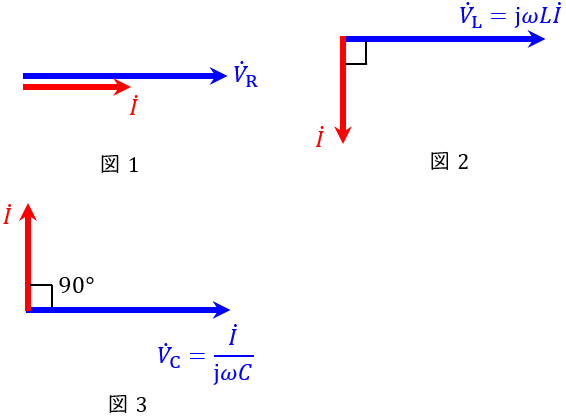
1.抵抗，コイル，コンデンサの電圧\( \ V \ \mathrm {[V]} \ \)と電流\( \ I \ \mathrm {[A]} \ \)の関係
抵抗\( \ R \ \mathrm {[\Omega ]} \ \)，コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源の角周波数\( \ \omega \ \mathrm {[rad / s]} \ \)及び周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのインピーダンスは，
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {R}}&=&R&& \\[ 5pt ] {\dot Z}_{\mathrm {L}}&=&\mathrm {j}\omega L&=&\mathrm {j}2\pi f L \\[ 5pt ] {\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C}&=&\frac {1}{\mathrm {j}2\pi f C} \\[ 5pt ] \end{eqnarray}
\] で求められ，それぞれの電圧と電流の関係は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {R}}&=&R\dot I \\[ 5pt ] {\dot V}_{\mathrm {L}}&=&\mathrm {j}\omega L \dot I \\[ 5pt ] {\dot V}_{\mathrm {C}}&=&\frac {\dot I }{\mathrm {j}\omega C} \\[ 5pt ] \end{eqnarray}
\] となります。この関係をベクトル図に表すと，図1～図3となります。

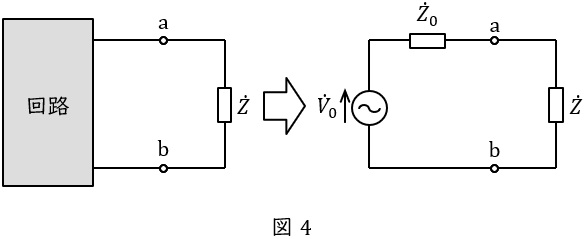
2.テブナンの定理
図4のように複雑な回路を電圧源\( \ {\dot V}_{0} \ \mathrm {[V]} \ \)とインピーダンス\( \ {\dot Z}_{0} \ \mathrm {[\Omega ]} \ \)に置き換える方法です。
\( \ {\dot V}_{0} \ \mathrm {[V]} \ \)は端子\( \ \mathrm {a} \ – \ \mathrm {b} \ \)の開放電圧，\( \ {\dot Z}_{0} \ \mathrm {[\Omega ]} \ \)は端子\( \ \mathrm {a} \ – \ \mathrm {b} \ \)から電源側回路を見た合成インピーダンスとなります。
ただし，\( \ {\dot Z}_{0} \ \mathrm {[\Omega ]} \ \)を求める際，電圧源は短絡，電流源は開放します。

【解答】

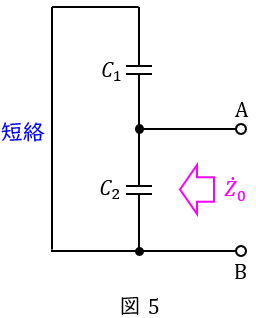
(1)解答：チ
図5の通り，負荷を開放し電源を短絡したときの端子\( \ \mathrm {A-B} \ \)から電源側をみたインピーダンス\( \ {\dot Z}_{0} \ \)は，コンデンサの並列回路であるから，
\[
\begin{eqnarray}
{\dot Z}_{0}&=&\frac {1}{j\omega \left( C_{1}+C_{2}\right) } \\[ 5pt ] \end{eqnarray}
\] と求められる。

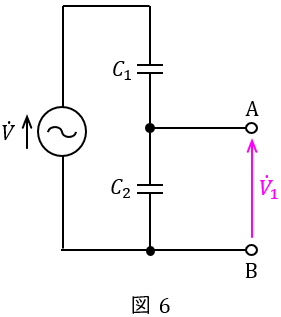
(2)解答：ル
図6の通り，負荷を開放したとき端子\( \ \mathrm {A-B} \ \)間に現れる電圧を\( \ {\dot V}_{1} \ \)とすると，分圧の法則より，
\[
\begin{eqnarray}
{\dot V}_{1}&=&\frac {\displaystyle \frac {1}{j\omega C_{2}}}{\displaystyle \frac {1}{j\omega C_{1}}+\frac {1}{j\omega C_{2}}}\dot V \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{C_{2}}}{\displaystyle \frac {1}{C_{1}}+\frac {1}{C_{2}}}\dot V \\[ 5pt ] &=&\frac {\displaystyle \frac {1}{C_{2}}}{\displaystyle \frac {C_{1}+C_{2}}{C_{1}C_{2}}}\dot V \\[ 5pt ] &=&\frac {\displaystyle 1}{\displaystyle \frac {C_{1}+C_{2}}{C_{1}}}\dot V \\[ 5pt ] &=&\frac {C_{1}}{C_{1}+C_{2}}\dot V \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ロ
(1)及び(2)解答式より，
\[
\begin{eqnarray}
{\dot V}_{2} &=&\frac {\dot Z}{{\dot Z}_{0}+r+j\omega L+\dot Z}\times {\dot V}_{1} \\[ 5pt ] &=&\frac {\dot Z}{\displaystyle \frac {1}{j\omega \left( C_{1}+C_{2}\right) }+r+j\omega L+\dot Z} \times \frac {C_{1}}{C_{1}+C_{2}}\dot V \\[ 5pt ] &=&\frac {1}{\displaystyle \frac {1}{\dot Z}\left[ \frac {1}{j\omega \left( C_{1}+C_{2}\right) }+r+j\omega L+\dot Z\right] } \times \frac {C_{1}}{C_{1}+C_{2}}\dot V \\[ 5pt ] &=&\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle \frac {1}{\dot Z}\left[ \dot Z+r+j\omega L-j\frac {1}{\omega \left( C_{1}+C_{2}\right) }\right] } \times \dot V \\[ 5pt ] &=&\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1+\frac {r}{\dot Z}+j\frac {1}{\dot Z}\left[ \omega L -\frac {1}{\omega \left( C_{1}+C_{2}\right) }\right] } \times \dot V \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ワ
\( \ \omega ^{2}L\left( C_{1}+C_{2} \right) =1 \ \)を変形すれば\( \ \omega L=\displaystyle \frac {1}{\omega \left( C_{1}+C_{2}\right) } \ \)となり，この条件を満たすとき\( \ {\dot V}_{2} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{2} &=&\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1+\frac {r}{\dot Z}+j\frac {1}{\dot Z}\left[ \omega L -\frac {1}{\omega \left( C_{1}+C_{2}\right) }\right] } \times \dot V \\[ 5pt ] &=&\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1+\frac {r}{\dot Z}+j\frac {1}{\dot Z}\times 0 } \times \dot V \\[ 5pt ] &=&\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1+\frac {r}{\dot Z}} \times \dot V \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ホ
(4)解答式において，\( \ r≪\left| \dot Z \right| \ \)とすれば，
\[
\begin{eqnarray}
{\dot V}_{2} &=&\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1+\frac {r}{\dot Z}} \times \dot V \\[ 5pt ] &≃&\frac {C_{1}}{C_{1}+C_{2}}\times \frac {1}{\displaystyle 1+0} \times \dot V \\[ 5pt ] &=&\frac {C_{1}}{C_{1}+C_{2}} \times \dot V \\[ 5pt ] \frac {\dot V}{{\dot V}_{2}}&=&\frac {C_{1}+C_{2}}{C_{1}} \\[ 5pt ] \frac {\left| \dot V \right| }{\left| {\dot V}_{2} \right| }&=&\frac {C_{1}+C_{2}}{C_{1}} \\[ 5pt ] \end{eqnarray}
\] と求められる。