《理論》〈電気回路〉[R03:問4]抵抗とリアクトルを組み合わせた三相交流回路に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，三相交流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選べ。

図1のように，実効値が$ \ 1 \ \mathrm {V} \ $である対称三相交流電源に，二つの$ \ \Delta \ $形不平衡負荷が並列接続されている。図1の各線間電圧は$ \ {\dot E}_{\mathrm {ab}}=1∠0° \ \mathrm {[V]} \ $を基準に$ \ {\dot E}_{\mathrm {bc}}=a^{2}{\dot E}_{\mathrm {ab}} \ $，$ \ {\dot E}_{\mathrm {ca}}=a{\dot E}_{\mathrm {ab}} \ $とする。ただし，$ \ a=\mathrm {e}^{\mathrm {j}\frac {2}{3}\pi } \ $である。

図2は，アドミタンス$ \ {\dot Y}_{\mathrm {ab}} \ $，$ \ {\dot Y}_{\mathrm {bc}} \ $及び$ \ {\dot Y}_{\mathrm {ca}} \ $を用いて表した図1の等価回路であり，$ \ {\dot Y}_{\mathrm {ab}} \ $及び$ \ {\dot Y}_{\mathrm {ca}} \ $は$ \ \fbox {　（１）　} \ \mathrm {S} \ $，$ \ {\dot Y}_{\mathrm {bc}} \ $は$ \ \fbox {　（２）　} \ \mathrm {S} \ $となる。

線電流$ \ {\dot I}_{\mathrm {a}} \ $の実効値及び位相角を求めると，それぞれ$ \ \fbox {　（３）　} \ \mathrm {A} \ $及び$ \ \fbox {　（４）　} \ ° \ $となる。ただし，位相角の符号は進みを正とする。

図1で消費する有効電力は$ \ \fbox {　（５）　} \ \mathrm {W} \ $である。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {5\sqrt {3}}{3}　　　　　&（ロ）&　-45　　　　　&（ハ）&　\frac {\sqrt {3}}{3}\mathrm {e}^{-\mathrm {j}\frac {1}{3}\pi } \\[ 5pt ] &（ニ）&　2\sqrt {3}\mathrm {e}^{-\mathrm {j}\frac {1}{3}\pi }　　　　　&（ホ）&　\sqrt {3}\mathrm {e}^{-\mathrm {j}\frac {1}{3}\pi }　　　　　&（ヘ）&　\sqrt {3} \\[ 5pt ] &（ト）&　\frac {5\sqrt {3}}{2}　　　　　&（チ）&　\frac {\sqrt {3}}{3}\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }　　　　　&（リ）&　2 \\[ 5pt ] &（ヌ）&　-90　　　　　&（ル）&　\frac {2\sqrt {3}}{3}\mathrm {e}^{-\mathrm {j}\frac {2}{3}\pi }　　　　　&（ヲ）&　\frac {5\sqrt {3}}{6} \\[ 5pt ] &（ワ）&　-60　　　　　&（カ）&　2\sqrt {3}　　　　　&（ヨ）&　\frac {2\sqrt {3}}{3}\mathrm {e}^{-\mathrm {j}\frac {1}{3}\pi } \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

不平衡負荷の三相交流回路に関する問題です。
三相不平衡負荷ですが，三相交流回路の問題は難易度が高い問題が出題されることが多いですが，この年は$ \ \Delta -\mathrm {Y} \ $変換や難解なベクトル演算等が不要で，例年に比べると易しい問題となります。

1.ベクトルオペレータ$ \ a \ $
ベクトルオペレータ$ \ a \ $は，$ \ a=e^{\mathrm {j}\frac {2\pi}{3}} \ $で定義される演算子であり，
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ] &=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ] &=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ] &=& 1 \\[ 5pt ] \end{eqnarray}
\] となります。上記より，
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ] 1+a+a^{2}&=& 0 \\[ 5pt ] \end{eqnarray}
\] の関係があることがわかります。

【解答】

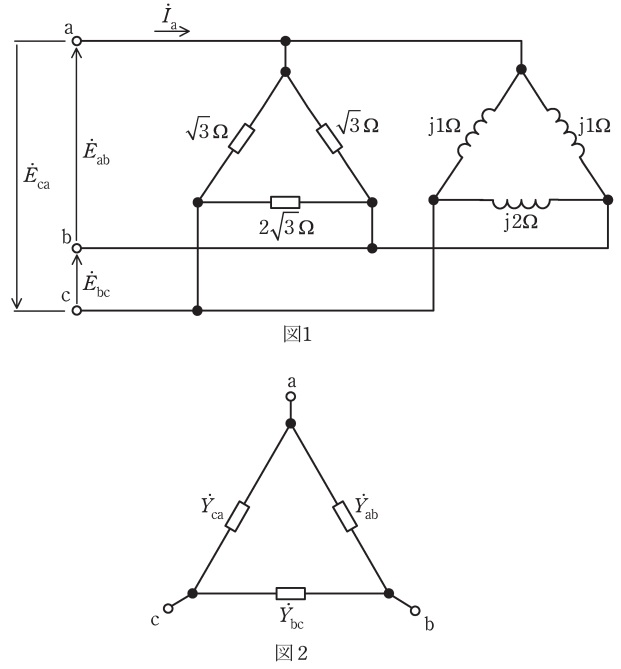
(1)解答：ヨ
図1-1に示す閉回路について考えると，$ \ {\dot Y}_{\mathrm {ab}} \ $は$ \ \sqrt {3} \ \mathrm {\Omega } \ $と$ \ \mathrm {j}1 \ \mathrm {\Omega } \ $の並列回路の合成アドミタンスであることがわかる。したがって，
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {ab}} &=& \frac {1}{\sqrt {3}}+\frac {1}{\mathrm {j}1} \\[ 5pt ] &=& \frac {1}{\sqrt {3}}-\mathrm {j} \\[ 5pt ] &=& \frac {2}{\sqrt {3}}\left( \frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}\right) \\[ 5pt ] &=& \frac {2}{\sqrt {3}}\mathrm {e}^{-\mathrm {j}\frac {1}{3}\pi } \\[ 5pt ] &=& \frac {2\sqrt {3}}{3}\mathrm {e}^{-\mathrm {j}\frac {1}{3}\pi } \ \mathrm {[S]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

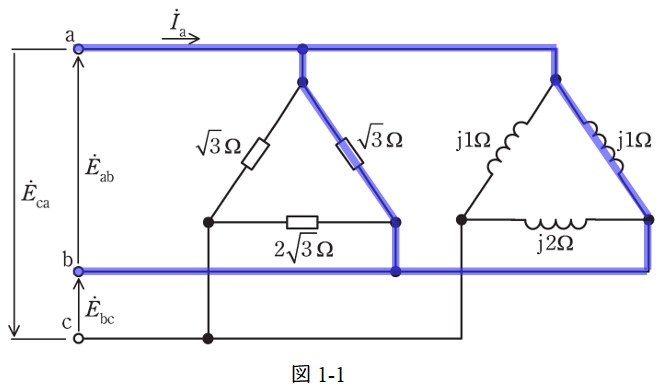
(2)解答：ハ
(1)と同様に，図1-2に示す閉回路について考えると，$ \ {\dot Y}_{\mathrm {bc}} \ $は$ \ 2\sqrt {3} \ \mathrm {\Omega } \ $と$ \ \mathrm {j}2 \ \mathrm {\Omega } \ $の並列回路の合成アドミタンスであることがわかる。したがって，
\[
\begin{eqnarray}
{\dot Y}_{\mathrm {bc}} &=& \frac {1}{2\sqrt {3}}+\frac {1}{\mathrm {j}2} \\[ 5pt ] &=& \frac {1}{2\sqrt {3}}-\mathrm {j}\frac {1}{2} \\[ 5pt ] &=& \frac {1}{\sqrt {3}}\left( \frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}\right) \\[ 5pt ] &=& \frac {1}{\sqrt {3}}\mathrm {e}^{-\mathrm {j}\frac {1}{3}\pi } \\[ 5pt ] &=& \frac {\sqrt {3}}{3}\mathrm {e}^{-\mathrm {j}\frac {1}{3}\pi } \ \mathrm {[S]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：リ
図2の$ \ {\dot Y}_{\mathrm {ab}} \ $を流れる電流$ \ {\dot I}_{\mathrm {ab}} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {ab}} &=& {\dot Y}_{\mathrm {ab}}{\dot E}_{\mathrm {ab}} \\[ 5pt ] &=& \left( \frac {1}{\sqrt {3}}-\mathrm {j}\right) \times 1 \\[ 5pt ] &=& \frac {1}{\sqrt {3}}-\mathrm {j} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であり，$ \ {\dot Y}_{\mathrm {ca}} \ $を流れる電流$ \ {\dot I}_{\mathrm {ca}} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {ca}} &=& {\dot Y}_{\mathrm {ca}}{\dot E}_{\mathrm {ca}} \\[ 5pt ] &=& \left( \frac {1}{\sqrt {3}}-\mathrm {j}\right) \times \left( -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2}\right) \\[ 5pt ] &=& -\frac {1}{2\sqrt {3}}+\frac {\sqrt {3}}{2}+\mathrm {j}\left( \frac {1}{2}+\frac {1}{2}\right) \\[ 5pt ] &=& \frac {\sqrt {3}}{3}+\mathrm {j} \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるから$ \ {\dot I}_{\mathrm {a}} \ \mathrm {[A]} \ $は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=& {\dot I}_{\mathrm {ab}}-{\dot I}_{\mathrm {ca}} \\[ 5pt ] &=& \frac {1}{\sqrt {3}}-\mathrm {j}-\left( \frac {\sqrt {3}}{3}+\mathrm {j}\right) \\[ 5pt ] &=& \frac {\sqrt {3}}{3}-\mathrm {j}-\frac {\sqrt {3}}{3}-\mathrm {j} \\[ 5pt ] &=& -\mathrm {j}2 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，$ \ {\dot I}_{\mathrm {a}} \ $の実効値は$ \ 2 \ \mathrm {A} \ $と求められる。

(4)解答：ヌ
(3)解答式の通り，$ \ {\dot I}_{\mathrm {a}} \ $の位相角は$ \ -90 \ ° \ $と求められる。

(5)解答：ヲ
$ \ \left| {\dot E}_{\mathrm {ab}}\right| = \left| {\dot E}_{\mathrm {bc}}\right| = \left| {\dot E}_{\mathrm {ca}}\right| = 1 \ \mathrm {[V]} \ $であるから，図1の各抵抗にかかる電圧の大きさはいずれも$ \ 1 \ \mathrm {V} \ $である。したがって，消費する有効電力$ \ P \ \mathrm {[W]} \ $は，
\[
\begin{eqnarray}
P &=& \frac {1^{2}}{\sqrt {3}}+\frac {1^{2}}{2\sqrt {3}}+\frac {1^{2}}{\sqrt {3}} \\[ 5pt ] &=& \frac {5}{2\sqrt {3}} \\[ 5pt ] &=& \frac {5\sqrt {3}}{6} \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] と求められる。