【問題】
【難易度】★★☆☆☆(やや易しい)
昇圧チョッパの動作モードに関して,次の問に答えよ。
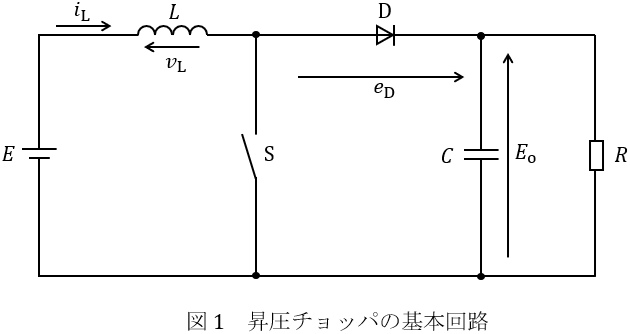
図1は昇圧チョッパの基本回路であり,一定電圧\( \ E \ \)の直流電源,インダクタンス\( \ L \ \)のリアクトル,静電容量\( \ C \ \)のコンデンサ,理想ダイオード\( \ \mathrm {D} \ \),スイッチ\( \ \mathrm {S} \ \)から構成される。抵抗\( \ R \ \)は負荷抵抗を表す。静電容量\( \ C \ \)は十分に大きく,出力電圧\( \ E_{\mathrm {o}} \ \)のリプルは無視できる。リアクトル電流と電圧をそれぞれ\( \ i_{\mathrm {L}} \ \)と\( \ v_{\mathrm {L}} \ \),\( \ \mathrm {D} \ \)の逆電圧を\( \ e_{\mathrm {D}} \ \)とする。図2は昇圧チョッパ回路の各部の電圧電流波形を示し,横軸は時間である。\( \ d \ \)は\( \ \mathrm {S} \ \)のスイッチング周期\( \ T \ \)に対するオン期間\( \ T_{\mathrm {ON}} \ \)の比であり,\( \ \displaystyle d=\frac {T_{\mathrm {ON}}}{T} \ \)である。図1の回路は\( \ d \ \)を一定で駆動される。
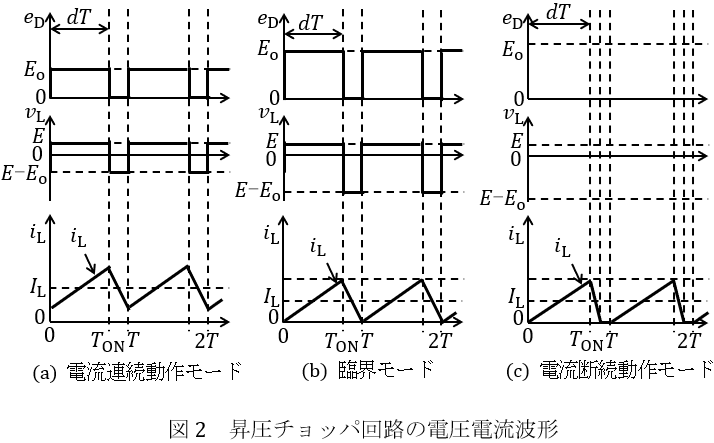
図2(a)は\( \ i_{\mathrm {L}} \ \)が連続する電流連続動作モードの場合である。\( \ \mathrm {S} \ \)がオンすると\( \ i_{\mathrm {L}} \ \)は直線的に増加し,\( \ \mathrm {S} \ \)がオフすると\( \ i_{\mathrm {L}} \ \)は直線的に減少する。\( \ I_{\mathrm {L}} \ \)は\( \ i_{\mathrm {L}} \ \)の平均値である。
(1) \( \ \mathrm {S} \ \)のオン期間中及びオフ期間中の\( \ i_{\mathrm {L}} \ \)の傾きを求めよ。
(2) \( \ E_{\mathrm {o}} \ \)を\( \ E \ \)と\( \ d \ \)を用いて表せ。
図2(b)は電流連続動作モードと\( \ i_{\mathrm {L}} \ \)が断続する電流断続動作モードの境界の臨界モードの場合であり,\( \ i_{\mathrm {L}} \ \)の最大値は平均値\( \ I_{\mathrm {L}} \ \)の\( \ 2 \ \)倍である。
(3) \( \ I_{\mathrm {L}} \ \)を\( \ E \ \),\( \ L \ \),\( \ d \ \),\( \ T \ \)を用いて表せ。
(4) 直流電源からの入力電力と負荷抵抗での消費電力が等しいことを用いて,臨界モードとなる\( \ R \ \)を\( \ L \ \),\( \ d \ \),\( \ T \ \)を用いて表せ。
図2(c)は電流断続動作モードの場合であり,\( \ i_{\mathrm {L}} \ \)のみが描かれている。
(5) 図2(c)と同じものが答案用紙に描かれているので,このときの\( \ e_{\mathrm {D}} \ \)と\( \ v_{\mathrm {L}} \ \)の概形を答案用紙に太い線で明確に描け。
【ワンポイント解説】
昇圧チョッパの各動作モードにおける電圧や電流に関する問題です。
チョッパの動作原理をしっかりと理解していれば,短時間で高得点を狙える問題です。
パワーエレクトロニクスに関してはしっかりと中身を理解していくようにして下さい。
1.昇圧チョッパ
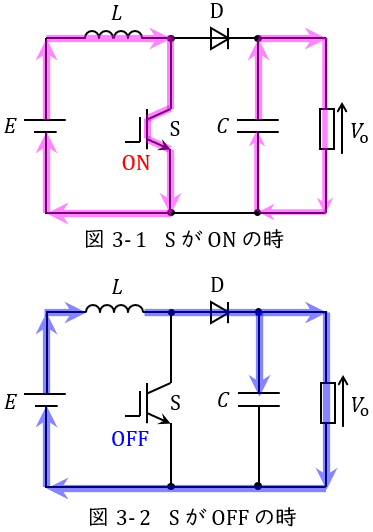
図3-1及び図3-2に昇圧チョッパの例を示します。
スイッチ\( \ \mathrm {S} \ \)が\( \ \mathrm {ON} \ \)時は図2-1のように導通し,電源\( \ E \ \)からリアクトル\( \ L \ \)にエネルギー\( \ EIT_{\mathrm {on}} \ \)が蓄えられ,出力側はコンデンサ\( \ C \ \)から電荷が供給されます。
スイッチ\( \ \mathrm {OFF} \ \)時は図2-2のように導通し,リアクトル\( \ L \ \)に蓄えられたエネルギー\( \ \displaystyle L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \ \)が放出されます。定常状態では蓄えられるエネルギーと放出するエネルギーが等しいので,
\[
\begin{eqnarray}
EIT_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}IT_{\mathrm {off}} \\[ 5pt ]
ET_{\mathrm {on}}&=&L\frac {\mathrm {d}i}{\mathrm {d}t}T_{\mathrm {off}} \\[ 5pt ]
L\frac {\mathrm {d}i}{\mathrm {d}t}&=&\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E \\[ 5pt ]
\end{eqnarray}
\]
となります。また回路方程式は,
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {o}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
E+L\frac {\mathrm {d}i}{\mathrm {d}t}&=&V_{\mathrm {o}} \\[ 5pt ]
E+\frac {T_{\mathrm {on}}}{T_{\mathrm {off}}}E&=&V_{\mathrm {o}} \\[ 5pt ]
V_{\mathrm {o}}&=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ]
\end{eqnarray}
\]
となり,通流率\( \ \displaystyle \gamma =\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}} \ \)を用いて表すと,
\[
\begin{eqnarray}
V_{\mathrm {0}} &=&\frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {off}}}E \\[ 5pt ]
&=&\frac {\displaystyle \frac {T_{\mathrm {on}}+T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}{\displaystyle \frac {T_{\mathrm {off}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ]
&=&\frac {1}{\displaystyle \frac {T_{\mathrm {on}}+T_{\mathrm {off}}-T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ]
&=&\frac {1}{\displaystyle 1-\frac {T_{\mathrm {on}}}{T_{\mathrm {on}}+T_{\mathrm {off}}}}E \\[ 5pt ]
&=&\frac {1}{\displaystyle 1-\gamma }E \\[ 5pt ]
\end{eqnarray}
\]
となります。
【解答】
(1)\( \ \mathrm {S} \ \)のオン期間中及びオフ期間中の\( \ i_{\mathrm {L}} \ \)の傾き
ターンオン期間中においては,
\[
\begin{eqnarray}
E&=&L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t} \\[ 5pt ]
\end{eqnarray}
\]
が成立するので,これを整理すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}&=&\frac {E}{L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。同様にターンオフ期間中においては,
\[
\begin{eqnarray}
E&=&L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}+E_{\mathrm {o}} \\[ 5pt ]
\end{eqnarray}
\]
が成立するので,これを整理すると,
\[
\begin{eqnarray}
L\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}&=&E-E_{\mathrm {o}} \\[ 5pt ]
\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}&=&\frac {E-E_{\mathrm {o}}}{L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ E_{\mathrm {o}} \ \)を\( \ E \ \)と\( \ d \ \)を用いて表す
(1)解答式より,定常状態においては,ターンオン期間中の電圧変化量とターンオフ期間中の電圧変化量は等しいので,
\[
\begin{eqnarray}
\frac {E}{L}T_{\mathrm {ON}}&=&-\frac {E-E_{\mathrm {o}}}{L}\left( T-T_{\mathrm {ON}}\right) \\[ 5pt ]
EdT&=&-\left( E-E_{\mathrm {o}}\right) \left( T-dT\right) \\[ 5pt ]
Ed&=&-\left( E-E_{\mathrm {o}}\right) \left( 1-d\right) \\[ 5pt ]
E-E_{\mathrm {o}}&=&-\frac {d}{1-d}E \\[ 5pt ]
E_{\mathrm {o}}&=&E+\frac {d}{1-d}E \\[ 5pt ]
&=&\frac {1-d+d}{1-d}E \\[ 5pt ]
&=&\frac {1}{1-d}E \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ I_{\mathrm {L}} \ \)を\( \ E \ \),\( \ L \ \),\( \ d \ \),\( \ T \ \)を用いて表す
(1)と同様に,ターンオン期間中においては,
\[
\begin{eqnarray}
\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}&=&\frac {E}{L} \\[ 5pt ]
\end{eqnarray}
\]
が成立し,図2(b)より,
\[
\begin{eqnarray}
\frac {\mathrm {d}i_{\mathrm {L}}}{\mathrm {d}t}&=&\frac {2I_{\mathrm {L}}}{dT} \\[ 5pt ]
\end{eqnarray}
\]
が成立するので,
\[
\begin{eqnarray}
\frac {E}{L}&=&\frac {2I_{\mathrm {L}}}{dT} \\[ 5pt ]
I_{\mathrm {L}}&=&\frac {EdT}{2L} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)臨界モードとなる\( \ R \ \)を\( \ L \ \),\( \ d \ \),\( \ T \ \)を用いて表す
題意より,直流電源からの入力電力と負荷抵抗での消費電力が等しいので,
\[
\begin{eqnarray}
EI_{\mathrm {L}}&=&\frac {{E_{\mathrm {o}}}^{2}}{R} \\[ 5pt ]
\end{eqnarray}
\]
となり,これに(2)解答式及び(3)解答式を代入して整理すると,
\[
\begin{eqnarray}
E\cdot \frac {EdT}{2L}&=&\frac {\displaystyle \left( \frac {1}{1-d}E\right) ^{2}}{R} \\[ 5pt ]
R&=&\left( \frac {1}{1-d}E\right) ^{2}\times \frac {2L}{E^{2}dT} \\[ 5pt ]
&=&\frac {2L}{d\left( 1-d\right) ^{2}T} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)電流断続動作モードの場合の\( \ e_{\mathrm {D}} \ \)と\( \ v_{\mathrm {L}} \ \)の概形
基本的には断続モードと同様に,ターンオン期間においては,
\[
\begin{eqnarray}
e_{\mathrm {D}} &=&E_{\mathrm {o}} \\[ 5pt ]
v_{\mathrm {L}}&=&E \\[ 5pt ]
\end{eqnarray}
\]
が成立し,ターンオフ期間においては,
\[
\begin{eqnarray}
e_{\mathrm {D}} &=&0 \\[ 5pt ]
v_{\mathrm {L}}&=&E-E_{\mathrm {o}} \\[ 5pt ]
\end{eqnarray}
\]
が成立する。電流断続期間においては,リアクトル\( \ L \ \)には電流が流れないので,
\[
\begin{eqnarray}
v_{\mathrm {L}}&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,回路の電圧の関係より,
\[
\begin{eqnarray}
E&=&v_{\mathrm {L}}-e_{\mathrm {D}}+E_{\mathrm {o}} \\[ 5pt ]
e_{\mathrm {D}}&=&E_{\mathrm {o}}-E \\[ 5pt ]
\end{eqnarray}
\]
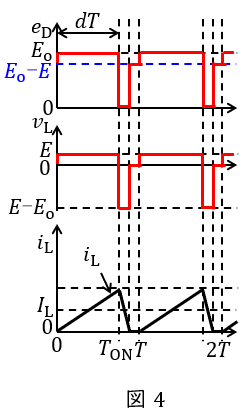
となる。したがって,電流断続動作モードの場合の\( \ e_{\mathrm {D}} \ \)と\( \ v_{\mathrm {L}} \ \)の概形は図4のようになる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん