《機械》〈変圧器〉[H27:問3] 単相変圧器の並行運転に関する計算・空欄穴埋問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，単相変圧器の並行運転に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。

負荷の増大に伴って変圧器を増設する場合，又は負荷変動に応じて変圧器の運転台数を変えて経済的な運転を図る場合に，変圧器の並行運転が行われる。単相変圧器の並行運転において，以下の配慮が必要である。

a.　各変圧器の$ \ \fbox {　（１）　} \ $を等しく，一次及び二次の定格電圧をそれぞれ等しくすることが望ましい。等しくない場合は各変圧器間に$ \ \fbox {　（２）　} \ $電流が流れ，変圧器が過熱したり，負荷に十分な電力を供給できない。

b.　結線にあたっては$ \ \fbox {　（３）　} \ $を合わせる。

c.　各変圧器がそれぞれの定格容量に比例して負荷電流を分担するためには，自己容量をベースとする百分率インピーダンス降下が近いものを用いる。百分率インピーダンス降下が大きく異なる場合は，定格容量に比例した負荷分担が不可能となる。

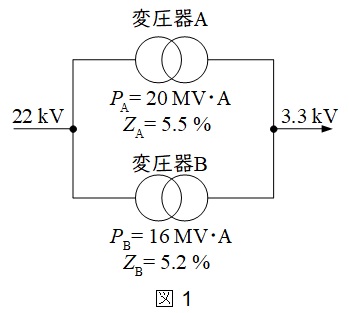
いま，一次定格電圧が$ \ 22 \ \mathrm {kV} \ $，及び二次定格電圧が$ \ 3.3 \ \mathrm {kV} \ $である2台の単相変圧器$ \ \mathrm {A} \ $及び$ \ \mathrm {B} \ $があり，定格容量及び百分率インピーダンス降下はそれぞれ変圧器$ \ \mathrm {A} \ $が$ \ 20 \ \mathrm {MV\cdot A} \ $，$ \ 5.5 \ ％ \ $，変圧器$ \ \mathrm {B} \ $が$ \ 16 \ \mathrm {MV\cdot A} \ $，$ \ 5.2 \ ％ \ $である。また，各変圧器の巻線抵抗の漏れリアクタンスに対する比は等しいものとする。これらの$ \ 2 \ $台の変圧器を並行運転して定格容量以内で供給できる最大負荷は$ \ \fbox {　（４）　} \ \mathrm {MV\cdot A} \ $であり，定格容量に達する変圧器は，$ \ \fbox {　（５）　} \ $である。

〔問3の解答群〕
\[
\begin{eqnarray}
&（イ）&　極　性　　　　　　　&（ロ）&　短絡比　　　　　　　&（ハ）&　\mathrm {A} \\[ 5pt ] &（ニ）&　負　荷　　　　　&（ホ）&　\mathrm {B}　　　　　&（ヘ）&　励　磁 \\[ 5pt ] &（ト）&　循　環　　　　　&（チ）&　34.9　　　　　&（リ）&　\mathrm {A} \ 及び \ \mathrm {B} \ の両方 \\[ 5pt ] &（ヌ）&　32.8　　　　　&（ル）&　定　格　　　　　&（ヲ）&　高電位 \\[ 5pt ] &（ワ）&　電　源　　　　　&（カ）&　巻数比　　　　　&（ヨ）&　36.0
\end{eqnarray}
\]

【ワンポイント解説】

変圧器の諸特性及び単位法に関する問題で，二種や三種でもよく出題されるレベルの問題です。したがって，合格のためには確実に得点しておきたい問題となります。

1.単位法におけるインピーダンスと定格容量の関係
定格容量 $ \ P_{\mathrm {B}} \ $，定格電圧 $ \ V_{\mathrm {B}} \ $であるとき，インピーダンス$ \ Z \ $を単位法で表すと，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]}&=&\frac {Z\left[ \Omega \right] }{Z_{\mathrm {B}}} \\[ 5pt ] &=&\frac {Z\left[ \Omega \right] P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}} \\[ 5pt ] \end{eqnarray}
\] となります。このとき，$ \ P_{\mathrm {B}} \ $ベースから$ \ P_{\mathrm {A}} \ $ベースへのインピーダンス変換は，
\[
Z_{\mathrm {A}} \ \mathrm {[p.u.]}=\frac {P_{\mathrm {A}}}{P_{\mathrm {B}}}Z_{\mathrm {B}} \ \mathrm {[p.u.]}
\] となります。

【解答】

(1)解答：カ
題意より，解答候補は（イ）極性，（ロ）短絡比，（ヘ）励磁，（カ）巻数比，等になると思いますが，一次及び二次電圧を等しくするためには，巻数比を揃えることが必要となります。

(2)解答：ト
題意より，解答候補は（ニ）負荷，（ヘ）励磁，（ト）循環，（ル）定格，（ワ）電源，になると思いますが，変圧器が不平衡の場合に変圧器間に流れる電流を循環電流と言います。

(3)解答：イ
題意より，解答候補は（イ）極性，（ロ）短絡比，（カ）巻数比，等になると思いますが，$ \ \Delta -\mathrm {Y} \ $結線や$ \ \mathrm {Y} -\Delta \ $結線で一次側及び二次側にて位相が$ \ 30° \ $ずれるので，極性を揃える必要があります。

(4)解答：チ
(5)解答：ホ
題意に沿って図を描くと図1のようになる。
変圧器$ \ \mathrm {A} \ $と変圧器$ \ \mathrm {B} \ $で定格容量が違うので，$ \ Z_{\mathrm {B}} \ $を$ \ 20 \ \mathrm {MV\cdot A} \ $ベースに変換すると，
\[
\begin{eqnarray}
Z_{\mathrm {B}}^{\prime }&=&\frac {20 \ \mathrm {MV\cdot A}}{16 \ \mathrm {MV\cdot A}}\times 5.2 \\[ 5pt ] &=&6.5 \ [％] \\[ 5pt ] \end{eqnarray}
\] となる。変圧器$ \ \mathrm {A} \ $と変圧器$ \ \mathrm {B} \ $の電圧降下は等しいので，ワンポイント解説「1.単位法におけるインピーダンスと定格容量の関係」より，
\[
\begin{eqnarray}
P_{\mathrm {A}}Z_{\mathrm {A}}&=&P_{\mathrm {B}}Z_{\mathrm {B}} \\[ 5pt ] 5.5P_{\mathrm {A}}&=&6.5P_{\mathrm {B}} \\[ 5pt ] \end{eqnarray}
\] となる。$ \ P_{\mathrm {A}} \ $が定格容量の$ \ 20 \ \mathrm {MV\cdot A} \ $で運転したとすると
\[
\begin{eqnarray}
5.5\times 20&=&6.5P_{\mathrm {B}} \\[ 5pt ] P_{\mathrm {B}}&≒&16.9 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] となるので，変圧器$ \ \mathrm {B} \ $は定格容量を超過してしまう。よって，$ \ P_{\mathrm {B}} \ $が定格容量の$ \ 16 \ \mathrm {MV\cdot A} \ $で運転したとすると，
\[
\begin{eqnarray}
5.5\times P_{\mathrm {A}}&=&6.5\times 16 \\[ 5pt ] P_{\mathrm {A}}&≒&18.9 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] となるので，その合計は，
\[
16+18.9=34.9 \ \mathrm {[MV\cdot A]}
\] と求められる。