【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,直流回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。
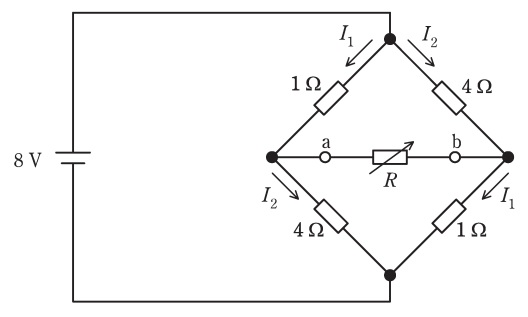
図の回路において,テブナンの定理に基づいて端子\( \ \mathrm {a} – \mathrm {b} \ \)から見た等価回路を考えれば,可変抵抗\( \ R \ \)の値が\( \ R= \ \fbox { (1) } \ \mathrm {\Omega } \ \)のとき可変抵抗\( \ R \ \)を流れる電流は\( \ 0.5 \ \mathrm {A} \ \)となり,また,可変抵抗\( \ R \ \)の値が\( \ R= \ \fbox { (2) } \ \mathrm {\Omega } \ \)のとき可変抵抗\( \ R \ \)で消費される電力は最大となることがわかる。
図の回路において,電圧源から見た回路の合成抵抗\( \ R_{0} \ \)は,可変抵抗\( \ R \ \)を用いて\( \ R_{0}= \ \fbox { (3) } \ \mathrm {[\Omega ]} \ \)と表せる。また,可変抵抗の値を\( \ R= \ \fbox { (4) } \ \mathrm {\Omega } \ \)とすれば,電圧源から見た回路の合成抵抗\( \ R_{0} \ \)の値は可変抵抗\( \ R \ \)の値と同じ値,すなわち\( \ R_{0}= \ \fbox { (4) } \ \mathrm {\Omega } \ \)となる。可変抵抗\( \ R \ \)の値を\( \ R= \ \fbox { (4) } \ \mathrm {\Omega } \ \)としたとき,図に示す電流\( \ I_{1} \ \)は,\( \ I_{1}= \ \fbox { (5) } \ \mathrm {A} \ \)となる。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& 1 &(ロ)& \frac {2}{3} &(ハ)& \frac {4}{5} \\[ 5pt ]
&(ニ)& \frac {5R+1}{R+5} &(ホ)& \frac {8}{5} &(ヘ)& 8 \\[ 5pt ]
&(ト)& \frac {4}{3} &(チ)& \frac {2R+9}{R+2} &(リ)& \frac {5R+8}{2R+5} \\[ 5pt ]
&(ヌ)& \frac {6}{5} &(ル)& 2 &(ヲ)& \frac {8}{3} \\[ 5pt ]
&(ワ)& 12 &(カ)& 3 &(ヨ)& 10 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
直流の電気回路の回路計算に関する問題です。本問は前半が比較的計算量が多く,後半が計算量が少なめのため,得点差が非常に出やすい問題となります。本問は1種で求められる計算内容が多く含まれているため,スラスラと完答できるぐらいのレベルになれるよう繰り返して下さい。
1.テブナンの定理
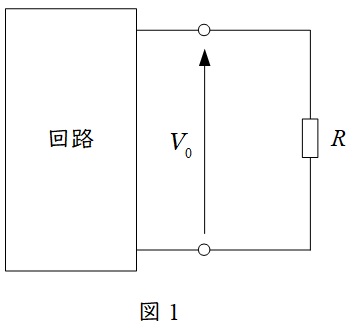
図1において回路中の2端子の開放電圧を\( \ V_{0} \ \),電圧源を短絡し,電流源を開放した時の端子から見た合成抵抗が\( \ R_{0} \ \)である時,外部抵抗\( \ R \ \)を接続すると,抵抗\( \ R \ \)を流れる電流\( \ I \ \)は,下式の通りとなります。
\[
\begin{eqnarray}
I&=&\frac {V_{0}}{R+R_{0}} \\[ 5pt ]
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)解答:ヘ
テブナンの定理に沿って,端子\( \ \mathrm {a} – \mathrm {b} \ \)の開放電圧を求める。分圧の法則より,端子\( \ \mathrm {a} \ \)の電圧\( \ V_{\mathrm {a}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {a}}&=&\frac {4}{1+4}\times 8 \\[ 5pt ]
&=&6.4 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
であり,端子\( \ \mathrm {b} \ \)の電圧\( \ V_{\mathrm {b}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {b}}&=&\frac {1}{1+4}\times 8 \\[ 5pt ]
&=&1.6 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,端子\( \ \mathrm {a} – \mathrm {b} \ \)の開放電圧\( \ V_{0} \ \)は,
\[
\begin{eqnarray}
V_{0}&=&V_{\mathrm {a}}-V_{\mathrm {b}} \\[ 5pt ]
&=&6.4-1.6 \\[ 5pt ]
&=&4.8 \ \mathrm {[V]} \\[ 5pt ]
\end{eqnarray}
\]
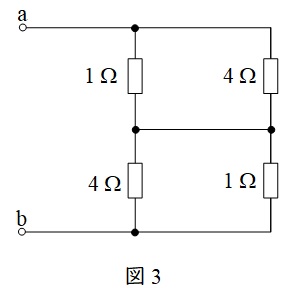
となる。次に,図2のように,電圧源を短絡した時の端子\( \ \mathrm {a} – \mathrm {b} \ \)から見た合成抵抗\( \ R_{\mathrm {ab}} \ \)は,図3のように書き換えられるので,
\[
\begin{eqnarray}
R_{\mathrm {ab}}&=&\frac {1\times 4}{1+4}+\frac {4\times 1}{1+4} \\[ 5pt ]
&=&1.6 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,ワンポイント解説「1.テブナンの定理」の通り,可変抵抗\( \ R \ \)を流れる電流\( \ I_{\mathrm {R}} \ \)が\( \ 0.5 \ \mathrm {[A]} \ \)になるためには,
\[
\begin{eqnarray}
I_{\mathrm {R}}&=&\frac {V_{0}}{R_{\mathrm {ab}}+R} \\[ 5pt ]
0.5&=&\frac {4.8}{1.6+R} \\[ 5pt ]
R&=&8 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。

(2)解答:ホ
可変抵抗\( \ R \ \)で消費される消費電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&R{I_{\mathrm {R}}}^{2} \\[ 5pt ]
&=&R\times \left( \frac {4.8}{1.6+R}\right) ^{2} \\[ 5pt ]
&=& \frac {23.04R}{R^{2}+3.2R+2.56} \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺\( \ R \ \)について微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}R}&=&\frac {23.04\left( R^{2}+3.2R+2.56\right) -23.04R \left( 2R+3.2\right) }{\left( R^{2}+3.2R+2.56\right) ^{2}} \\[ 5pt ]
&≒&\frac {-23.04R^{2}+58.98 }{\left( R^{2}+3.2R+2.56\right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。消費電力\( \ P \ \)が最大となるためには,\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}R}=0 \ \)である必要があるので,
\[
\begin{eqnarray}
-23.04R^{2}+58.98 &=&0 \\[ 5pt ]
R^{2} &≒&2.560 \\[ 5pt ]
R&≒&1.6 \ \mathrm {[\Omega ]} (∵R > 0)\\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:リ
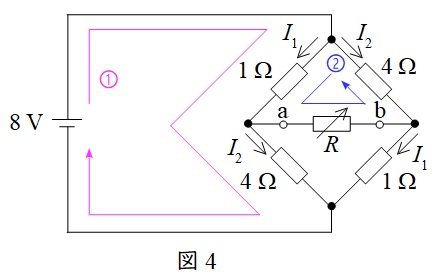
図4のように閉回路①及び②について回路方程式を求めると,
\[
\begin{eqnarray}
1\times I_{1}+4\times I_{2} &=&8 &&\\[ 5pt ]
I_{1}+4I_{2} &=&8 & ・・・・・・・・・・ ①&\\[ 5pt ]
1\times I_{1}+R\left( I_{1}-I_{2}\right)-4I_{2} &=&0 && \\[ 5pt ]
\left( 1+R\right) I_{1}-\left( 4+R\right)I_{2} &=&0 & ・・・・・・・・・・ ②& \\[ 5pt ]
\end{eqnarray}
\]
となり,①,②の連立方程式を解くと,
\[
\begin{eqnarray}
\left( 1+R\right) \left( 8-4I_{2}\right)-\left( 4+R\right) I_{2} &=&0&& \\[ 5pt ]
8-4I_{2}+8R-4RI_{2}-4I_{2}-RI_{2} &=&0&& \\[ 5pt ]
\left( 5R+8\right) I_{2} &=&8R+8&& \\[ 5pt ]
I_{2} &=&\frac {8R+8}{5R+8}&& \\[ 5pt ]
I_{1} &=&8-4I_{2}&& \\[ 5pt ]
&=&8-4\times \frac {8R+8}{5R+8} && \\[ 5pt ]
&=&\frac {8R+32}{5R+8} & ・・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となり,電源を流れる電流\( \ I_{0} \ \)は,
\[
\begin{eqnarray}
I_{0} &=&I_{1}+I_{2} \\[ 5pt ]
&=&\frac {8R+32}{5R+8}+\frac {8R+8}{5R+8} \\[ 5pt ]
&=&\frac {16R+40}{5R+8} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,全体の合成抵抗\( \ R_{0} \ \)は,
\[
\begin{eqnarray}
R_{0} &=&\frac {8}{I_{0}} \\[ 5pt ]
&=&8\times \frac {5R+8}{16R+40} \\[ 5pt ]
&=&\frac {5R+8}{2R+5} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ル
\( \ R_{0} \ \)と\( \ R \ \)が同じ値となるためには,
\[
\begin{eqnarray}
\frac {5R+8}{2R+5} &=&R \\[ 5pt ]
5R+8&=&2R^{2}+5R \\[ 5pt ]
R^{2}&=&4 \\[ 5pt ]
R&=&2 \ \mathrm {[\Omega ]}(∵R > 0) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
③式に\( \ R=2 \ \)を代入すると,
\[
\begin{eqnarray}
I_{1} &=&\frac {8R+32}{5R+8} \\[ 5pt ]
&=&\frac {8\times 2+32}{5\times 2+8} \\[ 5pt ]
&=&\frac {8}{3} \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん