《理論》〈電気回路〉[H24:問2]不平衡負荷のΔ-Y変換を用いた直流回路の解法に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，直流回路に関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も近いものを解答群の中から選びなさい。

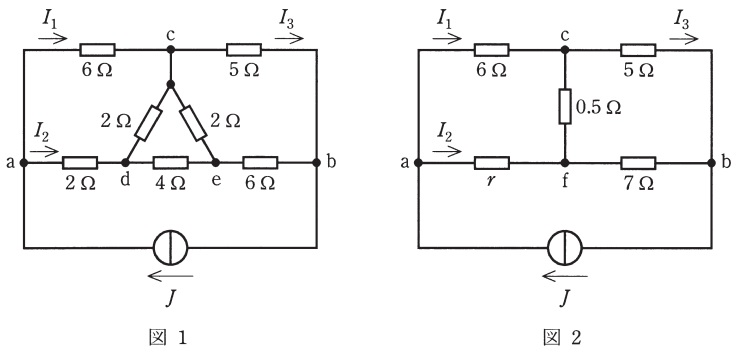
図1及び図2において，電流源の電流を$ \ J \ $とする。いま，図1の端子$ \ \mathrm {cde} \ $からなる$ \ \Delta \ $接続を$ \ \mathrm {Y} \ $接続に変換すると図2のように表され，$ \ r \ $は$ \ \fbox {　（１）　} \ \mathrm {[\Omega ]} \ $となる。

次に，図2の端子$ \ \mathrm {bcf} \ $からなる$ \ \Delta \ $接続を$ \ \mathrm {Y} \ $接続に変換して$ \ I_{1} \ $及び$ \ I_{2} \ $を求めれば，$ \ I_{1}=\fbox {　（２）　} \ \times J \ $，$ \ I_{2}=\fbox {　（３）　} \ \times J \ $となる。

一方，図2の経路$ \ \mathrm {acb} \ $と$ \ \mathrm {afb} \ $の電圧降下は等しいことから，$ \ I_{3} \ $は$ \ I_{3}=\fbox {　（４）　} \ \times J \ $となる。また，端子$ \ \mathrm {a-b} \ $間の電圧$ \ V_{\mathrm {ab}} \ $は，$ \ V_{\mathrm {ab}}=\fbox {　（５）　} \ \times J \ $となる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　0.271　　　　　　　&（ロ）&　0.346　　　　　　　&（ハ）&　0.355 \\[ 5pt ] &（ニ）&　0.548　　　　　&（ホ）&　0.574　　　　　&（ヘ）&　0.630 \\[ 5pt ] &（ト）&　0.645　　　　　&（チ）&　0.654　　　　　&（リ）&　0.728 \\[ 5pt ] &（ヌ）&　1　　　　　&（ル）&　2.59　　　　　&（ヲ）&　3 \\[ 5pt ] &（ワ）&　4　　　　　&（カ）&　4.87　　　&（ヨ）&　4.95 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {\Delta – Y} \ $変換を用いた直流回路の計算問題となります。
$ \ 1 \ $種の問題としては易しめの問題ではありますが，選択肢が絞れないので，前半で計算間違いをしてしまうと後半も連鎖的に間違えてしまう可能性があります。
慎重に計算して，完答できるように勉強を進めて下さい。

1.不平衡負荷の$ \ \mathrm {\Delta – Y} \ $変換と$ \ \mathrm {Y – \Delta} \ $変換
一種ではほぼ毎年，不平衡負荷の変換を使用する問題が出題されます。導出できる過程も重要ではありますが，暗記項目として覚えるようにしましょう。
a.$ \ \mathrm {\Delta – Y} \ $変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {b}} &=& \frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] {\dot Z}_{\mathrm {c}} &=& \frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ] \end{eqnarray}
\] b.$ \ \mathrm {Y – \Delta} \ $変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ] {\dot Z}_{\mathrm {bc}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ] {\dot Z}_{\mathrm {ca}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ] \end{eqnarray}
\]

【解答】

(1)解答：ヲ
図2において，$ \ \mathrm {\Delta – Y} \ $変換後の$ \ 0.5 \ \mathrm {\Omega } \ $及び$ \ 7 \ \mathrm {\Omega } \ $は求められているので，ワンポイント解説「1.不平衡負荷の$ \ \mathrm {\Delta – Y} \ $変換と$ \ \mathrm {Y – \Delta} \ $変換」に沿って$ \ r \ $を求めると，
\[
\begin{eqnarray}
r &=& \frac {2\times 4}{2+2+4} +2 \\[ 5pt ] &=& 1 +2 \\[ 5pt ] &=& 3 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ロ
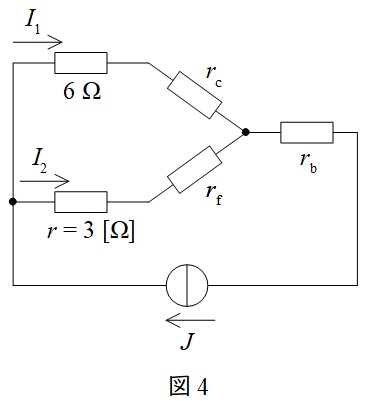
図2の端子$ \ \mathrm {bcf} \ $からなる$ \ \Delta \ $接続を$ \ \mathrm {Y} \ $接続に変換した図を図4に示す。図4における各抵抗の大きさは，ワンポイント解説「1.不平衡負荷の$ \ \mathrm {\Delta – Y} \ $変換と$ \ \mathrm {Y – \Delta} \ $変換」の通り，
\[
\begin{eqnarray}
r_{\mathrm {c}} &=& \frac {0.5\times 5}{0.5+7+5} \\[ 5pt ] &=& 0.2 \ \mathrm {[\Omega ]} \\[ 5pt ] r_{\mathrm {f}} &=& \frac {0.5\times 7}{0.5+7+5} \\[ 5pt ] &=& 0.28 \ \mathrm {[\Omega ]} \\[ 5pt ] r_{\mathrm {b}} &=& \frac {5\times 7}{0.5+7+5} \\[ 5pt ] &=& 2.8 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となる。分流の法則により$ \ I_{1} \ $を求めると，
\[
\begin{eqnarray}
I_{\mathrm {1}} &=& \frac {r+r_{\mathrm {f}}}{\left( 6+r_{\mathrm {c}}\right) +\left( r+r_{\mathrm {f}}\right) }J \\[ 5pt ] &=& \frac {3+0.28}{\left( 6+0.2\right) +\left( 3+0.28\right) }J \\[ 5pt ] &≒& 0.34599J　→　0.346J \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：チ
(2)と同様に，分流の法則により$ \ I_{2} \ $を求めると，
\[
\begin{eqnarray}
I_{\mathrm {2}} &=& \frac {6+r_{\mathrm {c}}}{\left( 6+r_{\mathrm {c}}\right) +\left( r+r_{\mathrm {f}}\right) }J \\[ 5pt ] &=& \frac {6+0.2}{\left( 6+0.2\right) +\left( 3+0.28\right) }J \\[ 5pt ] &≒& 0.65400J　→　0.654J \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ホ
図2の経路$ \ \mathrm {acb} \ $の電圧降下を$ \ V_{1} \ $，経路$ \ \mathrm {afb} \ $の電圧降下を$ \ V_{2} \ $とすると，
\[
\begin{eqnarray}
V_{1} &=& 6I_{1}+5I_{3} \\[ 5pt ] &=& 6\times 0.34599J+5I_{3} \\[ 5pt ] &≒& 2.0759J+5I_{3} \\[ 5pt ] V_{2} &=& rI_{2}+7\left( J-I_{3}\right) \\[ 5pt ] &=& 3\times 0.65400J+7J-7I_{3} \\[ 5pt ] &=& 8.9620J-7I_{3} \\[ 5pt ] \end{eqnarray}
\] となる。$ \ V_{1} \ $と$ \ V_{2} \ $は等しいので，
\[
\begin{eqnarray}
2.0759J+5I_{3}&=& 8.9620J-7I_{3} \\[ 5pt ] 12I_{3} &=& 8.9620J-2.0759J \\[ 5pt ] I_{3}&≒& 0.57384J　→　0.574J \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヨ
端子$ \ \mathrm {a-b} \ $間の電圧$ \ V_{\mathrm {ab}} \ $は，$ \ V_{2} \ $と等しいので，
\[
\begin{eqnarray}
V_{\mathrm {ab}} &=& V_{2} \\[ 5pt ] &=& 8.9620J-7I_{3} \\[ 5pt ] &=& 8.9620J-7\times 0.57384J \\[ 5pt ] &≒& 4.9451J　→　4.95J \\[ 5pt ] \end{eqnarray}
\] と求められる。