【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,反動水車の吸出し管に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切な語句,式又は数値を解答群の中から選びなさい。
吸出し管とはランナ出口から放水面までの接続管をいい,次の二つの機能を持っている。
a.ランナ出口と放水面間の落差(位置エネルギー)を有効に利用する。
b.ランナから放出された水のもつ運動エネルギーを効率よく回収し,吸出し管出口の\( \ \fbox { (1) } \ \)を少なくする。
水車に働く総エネルギーに対する,ランナ出口から放出される水のもつ運動エネルギーの割合は,低速水車よりも高速水車になるほど大きいため,一般的に,高速で,\( \ \fbox { (2) } \ \)の水車では,吸出し管の設計や施工の良否が水車全体の効率に大きく影響する。
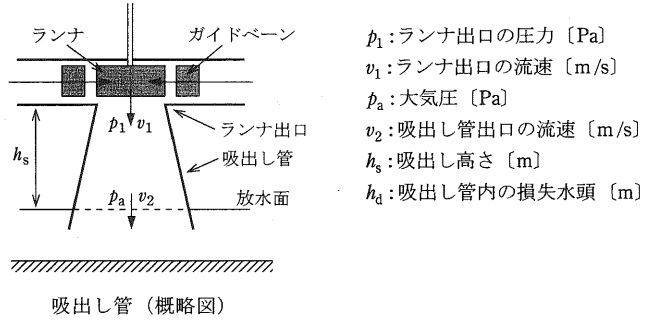
いま,図のように,ランナ出口の圧力,流速をそれぞれ\( \ p_{1} \ \mathrm {[Pa]} \ \),\( \ v_{1} \ \mathrm {[m / s]} \ \),吸出し管出口の流速を\( \ v_{2} \ \mathrm {[m / s]} \ \),大気圧を\( \ p_{\mathrm {a}} \ \mathrm {[Pa]} \ \),吸出し高さを\( \ h_{\mathrm {s}} \ \mathrm {[m]} \ \),吸出し管内における損失水頭を\( \ h_{\mathrm {d}} \ \mathrm {[m]} \ \),水の密度を\( \ \rho \ \mathrm {[kg / m^{3}]} \ \),重力加速度を\( \ g \ \mathrm {[m / s^{2}]} \ \)とすると,ベルヌーイの式より次式を導くことができる。
\[
\begin{eqnarray}
\frac {p_{1}}{\rho g} &=&\frac {p_{\mathrm {a}}}{\rho g}-h_{\mathrm {s}}-\left( \ \fbox { (3) } \ \right) \\[ 5pt ]
\end{eqnarray}
\]
\( \ \fbox { (3) } \ \)は,吸出し管で回収された運動エネルギー分を表し,この値が大きいほど\( \ \displaystyle \frac {p_{1}}{\rho g} \ \)が小さくなり水車出力は増加する。吸出し管の効率を\( \ \eta _{\mathrm {d}} \ \)とすると,回収された運動エネルギーに相当する水頭は\( \ \displaystyle \frac {\eta _{\mathrm {d}}{v_{1}}^{2}}{2g} \ \)で表され,\( \ \eta _{\mathrm {d}} \ \)は,普通,円すい形吸出し管で\( \ \fbox { (4) } \ \)程度,エルボ形で\( \ 0.6 \ \)程度である。
また,上式より,ランナ出口の圧力は大気圧より低くなるが,その値が水の蒸気圧より下がって蒸気の気泡が生じる現象を\( \ \fbox { (5) } \ \)と呼ぶ。
〔問2の解答群]
\[
\begin{eqnarray}
&(イ)& \frac {{v_{1}}^{2}}{2g}-\frac {{v_{2}}^{2}}{2g}-h_{\mathrm {d}} &(ロ)& キャビテーション &(ハ)& \frac {{v_{1}}^{2}}{2g}-\frac {{v_{2}}^{2}}{2g}+h_{\mathrm {d}} \\[ 5pt ]
&(ニ)& ハンチング &(ホ)& 低比速度 &(ヘ)& 高落差 \\[ 5pt ]
&(ト)& 0.4 &(チ)& 回復水頭 &(リ)& \frac {{v_{2}}^{2}}{2g}-\frac {{v_{1}}^{2}}{2g}+h_{\mathrm {d}} \\[ 5pt ]
&(ヌ)& 低落差 &(ル)& 0.1 &(ヲ)& サージング \\[ 5pt ]
&(ワ)& 廃棄損失 &(カ)& 圧力水頭 &(ヨ)& 0.8 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
反動水車の吸出し管に関する問題です。
比較的基本的な内容を問われている問題ですが,(2)や(3)のように,基本知識を前提として少し受験生に考えさせるように出題しているところが特徴的な問題です。
1.吸出し管
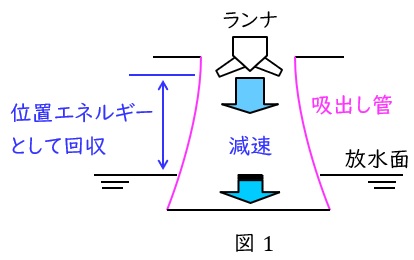
フランシス水車をはじめとする水が充満されている反動水車の出口に設けられる管で,図1に示すようなラッパ状の形をしたものが一般的です。
ランナで仕事をした水をそのまま放水口に出すのではなく,ランナから出た水の流路を広げランナ出口の圧力を大気圧以下に保持し,ラッパ状に広げ流速を落とすことで運動エネルギーを位置エネルギーとして回収します。
理論上の吸出し管の高さは大気圧(1気圧)である約\( \ 10.33 \ \mathrm {m} \ \)までですが,実際にはキャビテーション発生防止のため\( \ 7 \ \mathrm {m} \ \)程度までとしています。
2.ベルヌーイの定理
位置水頭が\( \ h \ \mathrm {[m]} \ \),圧力水頭が\( \ \displaystyle \frac {p}{\rho g} \ \mathrm {[m]} \ \),速度水頭が\( \ \displaystyle \frac {v^{2}}{2g} \ \mathrm {[m]} \ \)で表されるとき,これらの総和はエネルギー保存則によりどの場所でも等しくなります。
\[
\begin{eqnarray}
h+\frac {p}{\rho g}+\frac {v^{2}}{2g}&=&一定 \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ワ
題意より解答候補は,(チ)回復水頭,(ワ)廃棄損失,(カ)圧力水頭,等になると思います。
ワンポイント解説「1.吸出し管」の通り,吸出し管は運動エネルギーを位置エネルギーとして回収する設備で廃棄損失を少なくする役割があります。
(2)解答:ヌ
題意より解答候補は,(ホ)低比速度,(ヘ)高落差,(ヌ)低落差,等になると思います。
一般に低落差の設備の方が吸出し管の効率に占める割合が高くなり,吸出し管の設計や施工の良否が水車全体の効率に大きく影響します。
(3)解答:イ
題意より解答候補は,(イ)\( \ \displaystyle \frac {{v_{1}}^{2}}{2g}-\frac {{v_{2}}^{2}}{2g}-h_{\mathrm {d}} \ \),(ハ)\( \ \displaystyle \frac {{v_{1}}^{2}}{2g}-\frac {{v_{2}}^{2}}{2g}+h_{\mathrm {d}} \ \),(リ)\( \ \displaystyle \frac {{v_{2}}^{2}}{2g}-\frac {{v_{1}}^{2}}{2g}+h_{\mathrm {d}} \ \),になると思います。
ワンポイント解説「2.ベルヌーイの定理」の通り,本問の内容に沿ってベルヌーイの定理を適用すると,
\[
\begin{eqnarray}
h_{\mathrm {s}}+\frac {p_{1}}{\rho g}+\frac {{v_{1}}^{2}}{2g}&=&0+h_{\mathrm {d}}+\frac {p_{\mathrm {a}}}{\rho g}+\frac {{v_{2}}^{2}}{2g} \\[ 5pt ]
\end{eqnarray}
\]
の関係が成立するので,\( \ \displaystyle \frac {p_{1}}{\rho g} \ \)について整理すれば,
\[
\begin{eqnarray}
\frac {p_{1}}{\rho g} &=&\frac {p_{\mathrm {a}}}{\rho g}-h_{\mathrm {s}}- \frac {{v_{1}}^{2}}{2g}+\frac {{v_{2}}^{2}}{2g}+h_{\mathrm {d}} \\[ 5pt ]
&=&\frac {p_{\mathrm {a}}}{\rho g}-h_{\mathrm {s}}-\left( \frac {{v_{1}}^{2}}{2g}-\frac {{v_{2}}^{2}}{2g}-h_{\mathrm {d}} \right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
(4)解答:ヨ
題意より解答候補は,(ト)\( \ 0.4 \ \),(ル)\( \ 0.1 \ \),(ヨ)\( \ 0.8 \ \),になると思います。
円すい形吸出し管はエルボ形にくらべ効率が高く,\( \ \eta _{\mathrm {d}} \ \)は\( \ 0.8 \ \)程度となります。
(5)解答:ロ
題意より解答候補は,(ロ)キャビテーション,(ニ)ハンチング,(ヲ)サージング,になると思います。
ワンポイント解説「1.吸出し管」の通り,水の蒸気圧より下がって蒸気の気泡が生じる現象をキャビテーションといいます。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん