【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,線路リアクタンスを補償する目的で,線路に直列に挿入される直列コンデンサに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
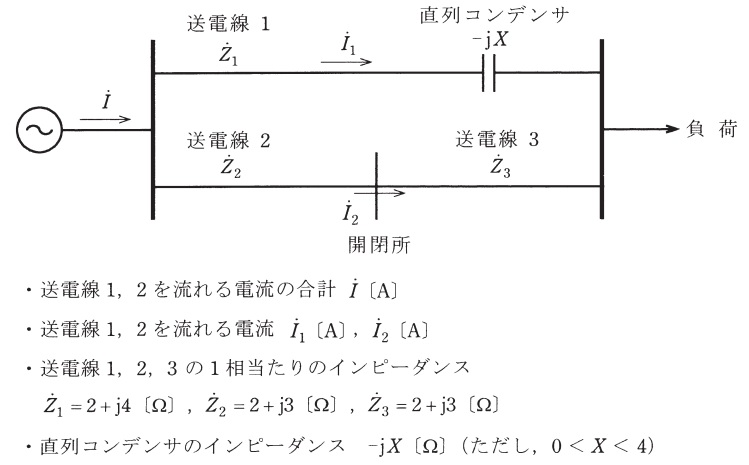
直列コンデンサを挿入することによる利点は,\( \ \fbox { (1) } \ \)の改善,\( \ \fbox { (2) } \ \),送電損失の低減などが挙げられる。一方,直列コンデンサの容量性リアクタンスは,\( \ \fbox { (3) } \ \)との関係において,軸ねじり振動を起こす可能性があり留意する必要がある。ここで,送電線\( \ 1 \ \)に直列コンデンサを挿入した図のような三相\( \ 3 \ \)線式送電系統の送電損失について考える。なお,送電線\( \ 2 \ \)と\( \ 3 \ \)は開閉所を介して接続されている。
送電損失\( \ \mathrm {[W]} \ \)(送電線\( \ 1~3 \ \)の合計)を,図中の記号及び下記のインピーダンス値を用いて表すと,\( \ \fbox { (4) } \ \)となる。また,送電線\( \ 2 \ \)を流れる電流\( \ {\dot I}_{2} \ \)は,\( \ \dot I \ \)と\( \ X \ \)を用いて表すと,\( \ \fbox { (5) } \ \)となる。同様に,送電線\( \ 1 \ \)の電流\( \ {\dot I}_{1} \ \)を,\( \ \dot I \ \)と\( \ X \ \)を用いて表し,\( \ \left| {\dot I}_{1}\right| \ \)と\( \ \left| {\dot I}_{2}\right| \ \)を\( \ \fbox { (4) } \ \)に代入すると,送電損失を\( \ \left| \dot I\right| \ \)と\( \ X \ \)を用いて表すことができる。
この式より,送電損失が最小となるように直列コンデンサのインピーダンスを設定する。そのときの送電損失\( \ \mathrm {[W]} \ \)を,\( \ \left| \dot I\right| \ \)を用いて表すと\( \ \fbox { (6) } \ \)であることが分かる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& 3\left( 2\left| {\dot I}_{1}\right| ^{2}+4\left| {\dot I}_{2}\right| ^{2}\right) &(ロ)& \frac {2+\mathrm {j}\left( 4-X\right) }{4+\mathrm {j}6}\dot I \\[ 5pt ]
&(ハ)& 2\left( \sqrt {5}\left| {\dot I}_{1}\right| ^{2}+\sqrt {13}\left| {\dot I}_{2}\right| ^{2}\right) &(ニ)& 2\left| {\dot I}_{1}\right| ^{2}+4\left| {\dot I}_{2}\right| ^{2} \\[ 5pt ]
&(ホ)& 5\left| \dot I\right| ^{2} &(ヘ)& 発電機調速機 \\[ 5pt ]
&(ト)& 電圧変動 &(チ)& 相関不平衡電圧 \\[ 5pt ]
&(リ)& 22\left| \dot I\right| ^{2} &(ヌ)& 送電線リアクタンス \\[ 5pt ]
&(ル)& 4\left| \dot I\right| ^{2} &(ヲ)& 励磁突入電流 \\[ 5pt ]
&(ワ)& \frac {4+\mathrm {j}6}{6+\mathrm {j}\left( 10-X\right) }\dot I &(カ)& 系統周波数特性定数 \\[ 5pt ]
&(ヨ)& \frac {2+\mathrm {j}\left( 4-X\right) }{6+\mathrm {j}\left( 10-X\right) }\dot I &(タ)& 深夜帯のフェランチ効果の低減 \\[ 5pt ]
&(レ)& 長距離送電線の安定度向上 &(ソ)& 短距離送電線の安定度向上 \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
直列コンデンサを挿入する目的,利点及び注意点に関する内容とその応用としての回路計算に関する問題となっています。(6)の計算は一種らしく複雑な計算が必要となります。
1.直列コンデンサを挿入する利点
①電圧変動(電圧降下)の改善
三相の送電線の電圧降下\( \ v \ \)は近似式として,
\[
\begin{eqnarray}
v&≒&\sqrt {3}I\left( R\cos \theta +X\sin \theta \right) \\[ 5pt ]
\end{eqnarray}
\]
となりますが,直列コンデンサを挿入することで\( \ X \ \)の値を小さくすることができ,電圧降下を小さくすることができます。
①安定度の向上
送電線の距離を電気的に小さくすることができるので定態安定度が向上し,電圧と電流の位相差が小さくなるので過渡安定度が向上します。
③送電損失の低減
本問のメインテーマとなっていますが,コンデンサを挿入することで,送電損失を低減することができます。
2.直列コンデンサを挿入する際の注意点
①タービン発電機との軸ねじれ現象
電力系統でのリアクトルとコンデンサによる電気的振動とタービン発電機軸の機械的振動が共振し,タービン軸に過剰な負担がかかる現象です。
②変圧器励磁時の共振現象
直列コンデンサと変圧器が鉄共振が発生する可能性があります。
③自己励磁現象
コンデンサの残留電荷により,自己励磁現象が発生する可能性があります。
【解答】
(1)解答:ト
題意より,解答候補は(ト)電圧変動,(チ)相関不平衡電圧,(ヌ)送電線リアクタンス,(ヲ)励磁突入電流,になると思います。(ト)電圧変動と(ヌ)送電線リアクタンスで迷うところですが,主な目的としては電圧変動の改善の方がより適当と言えると思います。
(2)解答:レ
題意より,解答候補は(タ)深夜帯のフェランチ効果の低減,(レ)長距離送電線の安定度向上,(ソ)短距離送電線の安定度向上,になると思います。ワンポイント解説「1.直列コンデンサを挿入する利点」の通り,直列コンデンサを挿入する利点は長距離送電線の安定度向上になります。短距離送電線はリアクタンスが小さいのでそこまで安定度を意識する必要はありません。
(3)解答:ヌ
題意より,解答候補は(ヘ)発電機調速機,(ヌ)送電線リアクタンス,(カ)系統周波数特性定数,になると思います。軸ねじり現象は送電線リアクタンスと直列コンデンサとの関係による電気的振動がタービン軸の機械的振動と共振を起こすことにより発生する現象となります。
(4)解答:イ
送電線\( \ 1 \ \),\( \ 2 \ \),\( \ 3 \ \)のインピーダンスをそれぞれ\( \ {\dot Z}_{1}=R_{1}+\mathrm {j}X_{1}=2+\mathrm {j}4 \ \),\( \ {\dot Z}_{2}=R_{2}+\mathrm {j}X_{2}=2+\mathrm {j}3 \ \),\( \ {\dot Z}_{3}=R_{3}+\mathrm {j}X_{3}=2+\mathrm {j}3 \ \)とおきます。
送電損失を\( \ P_{\mathrm {L}} \ \)とすると,
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&3R_{1}\left| {\dot I}_{1}\right| ^{2}+3R_{2}\left| {\dot I}_{2}\right| ^{2}+3R_{3}\left| {\dot I}_{2}\right| ^{2} \\[ 5pt ]
&=&3\times 3\left| {\dot I}_{1}\right| ^{2}+3\times 2\left| {\dot I}_{2}\right| ^{2}+3\times 2\left| {\dot I}_{2}\right| ^{2} \\[ 5pt ]
&=&3\left( 2\left| {\dot I}_{1}\right| ^{2}+4\left| {\dot I}_{2}\right| ^{2}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
(5)解答:ヨ
送電線\( \ 2 \ \)を流れる電流\( \ {\dot I}_{2} \ \)は,分流の法則より,
\[
\begin{eqnarray}
{\dot I}_{2}&=&\frac {{\dot Z}_{1}-\mathrm {j}X}{{\dot Z}_{1}-\mathrm {j}X+{\dot Z}_{2}+{\dot Z}_{3}}\times \dot I \\[ 5pt ]
&=&\frac {2+\mathrm {j}4-\mathrm {j}X}{2+\mathrm {j}4-\mathrm {j}X+2+\mathrm {j}3+2+\mathrm {j}3}\times \dot I \\[ 5pt ]
&=&\frac {2+\mathrm {j}\left( 4-X\right) }{6+\mathrm {j}\left( 10-X\right) }\dot I \\[ 5pt ]
\end{eqnarray}
\]
と求められます。
(6)解答:ル
送電線\( \ 2 \ \)と同様に送電線\( \ 1 \ \)を流れる電流\( \ {\dot I}_{1} \ \)は,分流の法則より,
\[
\begin{eqnarray}
{\dot I}_{1}&=&\frac {{\dot Z}_{2}+{\dot Z}_{3}}{{\dot Z}_{1}-\mathrm {j}X+{\dot Z}_{2}+{\dot Z}_{3}}\times \dot I \\[ 5pt ]
&=&\frac {2+\mathrm {j}3+2+\mathrm {j}3}{2+\mathrm {j}4-\mathrm {j}X+2+\mathrm {j}3+2+\mathrm {j}3}\times \dot I \\[ 5pt ]
&=&\frac {4+\mathrm {j}6}{6+\mathrm {j}\left( 10-X\right) }\dot I \\[ 5pt ]
\end{eqnarray}
\]
となり,(4)の解答式にそれぞれ代入すると,送電損失\( \ P_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&3\left( 2\left| {\dot I}_{1}\right| ^{2}+4\left| {\dot I}_{2}\right| ^{2}\right) \\[ 5pt ]
&=&3\left\{ 2\times \frac {4^{2}+6^{2}}{6^{2}+\left( 10-X\right) ^{2}}\left| \dot I\right| ^{2}+4\times \frac {2^{2}+\left( 4-X\right) ^{2}}{6^{2}+\left( 10-X\right) ^{2}}\left| \dot I\right| ^{2}\right\} \\[ 5pt ]
&=&\frac {312}{X^{2}-20X+136}\left| \dot I\right| ^{2}+\frac {12X^{2}-96X+240}{X^{2}-20X+136}\left| \dot I\right| ^{2} \\[ 5pt ]
&=&\frac {12X^{2}-96X+552}{X^{2}-20X+136}\left| \dot I\right| ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。両辺微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}P_{\mathrm {L}}}{\mathrm {d}X}&=&\frac {\left( 24X-96\right) \left( X^{2}-20X+136\right) -\left( 12X^{2}-96X+552\right) \left( 2X-20\right) }{\left( X^{2}-20X+136\right) ^{2}}\left| \dot I\right| ^{2} \\[ 5pt ]
&=&\frac {24X^{3}-576X^{2}+5184X-13056-\left( 24X^{3}-432X^{2}+3024X -11040\right) }{\left( X^{2}-20X+136\right) ^{2}}\left| \dot I\right| ^{2} \\[ 5pt ]
&=&\frac {-144X^{2}+2160X-2016}{\left( X^{2}-20X+136\right) ^{2}}\left| \dot I\right| ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となります。送電損失が最小となるためには,\( \ \displaystyle \frac {\mathrm {d}P_{\mathrm {L}}}{\mathrm {d}X}=0 \ \)である必要があるので,
\[
\begin{eqnarray}
-144X^{2}+2160X-2016&=&0 \\[ 5pt ]
X^{2}-15X+14&=&0 \\[ 5pt ]
\left( X-1\right) \left( X-14\right) &=&0 \\[ 5pt ]
X&=&1,14(不適) \\[ 5pt ]
\end{eqnarray}
\]
となります。この時,送電損失\( \ P_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {L}}&=&\frac {12\times 1^{2}-96\times 1+552}{1^{2}-20\times 1+136}\left| \dot I\right| ^{2} \\[ 5pt ]
&=&4\left| \dot I\right| ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められます。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん