《電力・管理》〈変電〉[H23:問3] 変電所における母線電圧算出に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

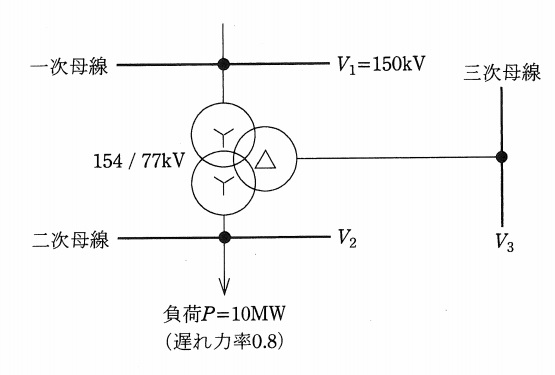
図のような\( \ P=10 \ \mathrm {[MW]} \ \)(遅れ力率\( \ 0.8 \ \))の負荷が接続された変電所において，変圧器の三次側にコンデンサ\( \ 30 \ \mathrm {[Mvar]} \ \)を設置した場合および設置しない場合の二次母線電圧を求めよ。
ただし，一次母線電圧は\( \ 150 \ \mathrm {[kV]} \ \)，容量，％インピーダンス及び使用タップの変圧器諸元は，次のとおりとし，変圧器の有効電力潮流による電圧降下分は無視できるものとする。また，計算においては，負荷電流は二次母線電圧が\( \ 77 \ \mathrm {[kV]} \ \)のとき\( \ 10 \ \mathrm {[MW]} \ \)となる電流，三次側のコンデンサの電流は三次母線電圧が\( \ 22 \ \mathrm {[kV]} \ \)のとき\( \ 30 \ \mathrm {[Mvar]} \ \)となる電流で一定とみなしてもよいものとする。
・容量　　　　　　　　一次側\( \ 100 \ \mathrm {[MV \cdot A]} \ \)
　　　　　　　　　　　二次側\( \ 100 \ \mathrm {[MV \cdot A]} \ \)
　　　　　　　　　　　三次側\( \ 30 \ \mathrm {[MV \cdot A]} \ \)
・％インピーダンス　　一次・二次間\( \ X_{12}=16 \ [％] \ ( \ 100 \ \mathrm {[MV \cdot A]} \ ベース \ )\)
　　　　　　　　　　　一次・三次間\( \ X_{31}= 8 \ [％] \ ( \ 100 \ \mathrm {[MV \cdot A]} \ ベース \ )\)
　　　　　　　　　　　二次・三次間\( \ X_{23}= 3 \ [％] \ ( \ 30 \ \mathrm {[MV \cdot A]} \ ベース \ )\)
・使用タップ　　　　　一次側\( \ 154 \ \mathrm {[kV]} \ \)
　　　　　　　　　　　二次側\( \ 77 \ \mathrm {[kV]} \ \)
　　　　　　　　　　　三次側\( \ 22 \ \mathrm {[kV]} \ \)

【ワンポイント解説】

各リアクトルを単位法で求め，さらに二次側電圧を求める計算量が多い難問です。ただし，抵抗分が無視できる時の系統の電圧特性の公式：\( \ V_{\mathrm {s}}=V_{\mathrm {r}}+X \cdot Q \ (各値はすべて[\mathrm {p.u.}]) \ \)を暗記していれば，電流を求めて計算をする必要がなくなり，幾分楽に解を求めることができます。二次試験では速く確実に解くことが求められますので，公式は暗記しておいた方が良いでしょう。

1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時，インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ] &=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}}　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.単位法における容量換算
「1.オーム法から単位法への変換」の通り，単位法のインピーダンスは基準容量に比例します。したがって，基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の単位法におけるインピーダンスは，
\[
\begin{eqnarray}
Z_{\mathrm {B}} \ \mathrm {[p.u.]}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}Z_{\mathrm {A}} \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

与えらえている各％インピーダンスを\( \ 100 \ \mathrm {[MV \cdot A]} \ \)ベースの単位法で表すと，
\[
\begin{eqnarray}
x_{12} \ \mathrm {[p.u.]}&=&\frac {16}{100} \\[ 5pt ] &=&0.16 \ \mathrm {[p.u.]} \\[ 5pt ] x_{31} \ \mathrm {[p.u.]}&=&\frac {8}{100} \\[ 5pt ] &=&0.08 \ \mathrm {[p.u.]} \\[ 5pt ] x_{23} \ \mathrm {[p.u.]}&=&\frac {3}{100} \times \frac {100}{30} \\[ 5pt ] &=&0.1 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。変圧器一次側，二次側，三次側のインピーダンスを\( \ x_{1} \ \)，\( \ x_{2} \ \)，\( \ x_{3} \ \)とすると，
\[
\begin{eqnarray}
x_{12}&=&x_{1}+x_{2} \\[ 5pt ] &=&0.16 \ \mathrm {[p.u.]} \\[ 5pt ] x_{31}&=&x_{3}+x_{1} \\[ 5pt ] &=&0.08 \ \mathrm {[p.u.]} \\[ 5pt ] x_{23}&=&x_{2}+x_{3} \\[ 5pt ] &=&0.1 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] という関係があるので，連立方程式を解くと各値は，
\[
\begin{eqnarray}
x_{1}&=&0.07 \ \mathrm {[p.u.]} \\[ 5pt ] x_{2}&=&0.09 \ \mathrm {[p.u.]} \\[ 5pt ] x_{3}&=&0.01 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。次に，負荷とコンデンサを\( \ 100 \ \mathrm {MV \cdot A} \ \)ベースの単位法で表す。
負荷の力率が\( \ 0.8 \ \)であるので，負荷の電力\( \ P+\mathrm {j}Q \ \)は，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&10+\mathrm {j} \frac {\sqrt {1-0.8^{2}}}{0.8}\times 10 \\[ 5pt ] &=&10+\mathrm {j}7.5 \ \mathrm {[MV\cdot A]} \\[ 5pt ] \end{eqnarray}
\] となる。よって負荷の\( \ 100 \ \mathrm {[MV \cdot A]} \ \)ベースの大きさは，
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&\frac {10}{100}+\mathrm {j}\frac {7.5}{100} \\[ 5pt ] &=&0.1+\mathrm {j}0.075 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。同様にコンデンサの\( \ 100 \ \mathrm {[MV \cdot A]} \ \)ベースの大きさ\( \ Q_{\mathrm {C}} \ \)は，
\[
\begin{eqnarray}
Q_{\mathrm {C}}&=&\frac {30}{100} \\[ 5pt ] &=&0.3 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。また，一次側電圧\( \ V_{1} \ \)を単位法で表すと，使用タップが\( \ 154 \ \mathrm {kV} \ \)であるから，
\[
\begin{eqnarray}
V_{1} \ \mathrm {[p.u.]}&=&\frac {150}{154} \\[ 5pt ] &≒&0.974 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。

(1)三次側にコンデンサを設置しない場合
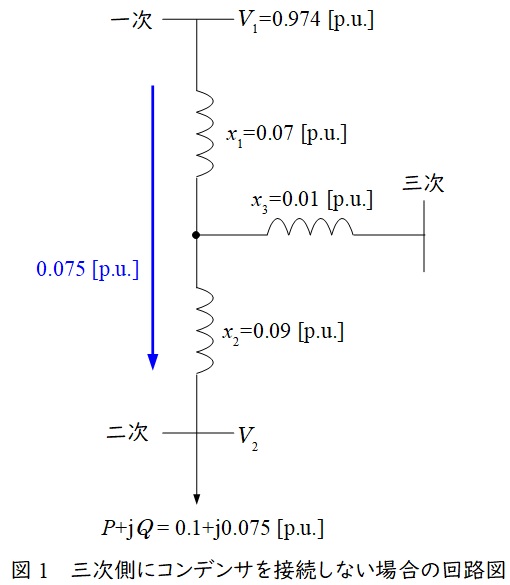
これまでの計算結果を整理したものを図1に示す。
題意より，変圧器の有効電力潮流による電圧降下分は無視できるので，リアクタンス降下は無効電力分のみ考慮すればよい。図1と電圧特性の公式より，
\[
\begin{eqnarray}
V_{1}&=&V_{2}+\left( x_{1} +x_{2} \right) Q \\[ 5pt ] \end{eqnarray}
\] ゆえに，
\[
\begin{eqnarray}
V_{2}&=&V_{1}-\left( x_{1} +x_{2} \right) Q \\[ 5pt ] &=&0.974-\left( 0.07 +0.09 \right) \times 0.075 \\[ 5pt ] &=&0.962 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] よって，二次側の電圧\( \ V_{2} \ \)は，
\[
\begin{eqnarray}
V_{2}&=&V_{2} \ \mathrm {[p.u.]}\times 77 \ \mathrm {[kV]} \\[ 5pt ] &=&0.962 \times 77 \\[ 5pt ] &≒&74.1 \ \mathrm {[kV]}\\[ 5pt ] \end{eqnarray}
\] と求められる。

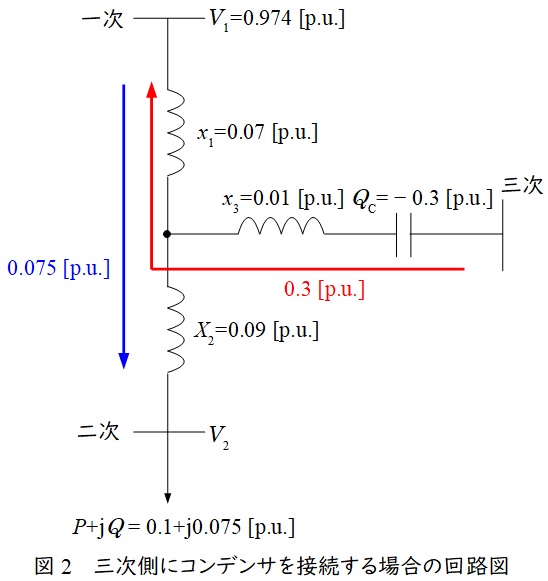
(2)三次側にコンデンサを設置する場合
図2にコンデンサを接続した場合の回路図を示す。
\( \ x_{1} \ \)を流れる無効電力は，
\[
\begin{eqnarray}
Q-Q_{\mathrm {C}}&=&0.075-0.3 \\[ 5pt ] &=&-0.225 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となるから，二次側の電圧\( \ V_{2} \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
V_{2}&=&V_{1}- x_{1}\left( Q-Q_{\mathrm {C}}\right)-x_{2}Q \\[ 5pt ] &=&0.974- 0.07\times \left(-0.225\right)-0.09\times 0.075 \\[ 5pt ] &=&0.983 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。よって，二次側の電圧\( \ V_{2} \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
V_{2}&=&V_{2} \ \mathrm {[p.u.]}\times 77 \ \mathrm {[kV]} \\[ 5pt ] &=&0.983 \times 77 \\[ 5pt ] &≒&75.7 \ \mathrm {[kV]}\\[ 5pt ] \end{eqnarray}
\] と求められる。