【問題】
【難易度】★★★★★(難しい)
図1に示すように,こう長\( \ 200 \ \mathrm {[km]} \ \)の\( \ 500 \ \mathrm {[kV]} \ \)並行\( \ 2 \ \)回線送電線で,送電端から\( \ 100 \ \mathrm {[km]} \ \)の地点に調相設備をもった中間開閉所がある送電系統を考える。送電線\( \ 1 \ \)回線のインダクタンスを\( \ 0.8 \ \mathrm {[mH/km]} \ \),静電容量を\( \ 0.01 \ \mathrm {[\mu F/km]} \ \)とし,送電線の抵抗分は無視できるとするとき,次の問に答えよ。
なお,周波数は\( \ 50 \ \mathrm {[Hz]} \ \)とし,単位法における基準容量は\( \ 1 \ 000 \ \mathrm {[MV\cdot A]} \ \),基準電圧は\( \ 500 \ \mathrm {[kV]} \ \)とする。また,円周率は,\( \ \pi =3.14 \ \)を用いよ。
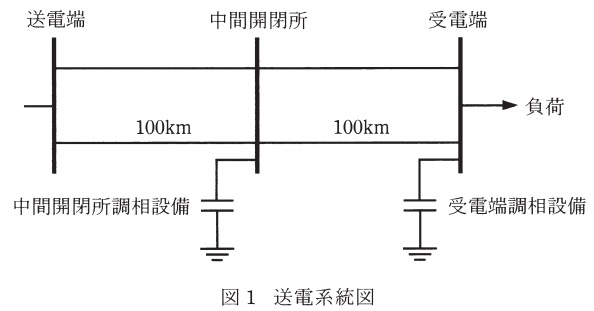
(1) 送電線\( \ 1 \ \)回線\( \ 1 \ \)区間(\( \ 100 \ \mathrm {[km]} \ \))を\( \ \pi \ \)形等価回路で,単位法で表した定数と併せて示せ。また,送電系統全体(負荷,調相設備を除く)の等価回路図を図2としたとき空白\( \ \mathrm {A~E} \ \)に当てはまる単位法で表した定数を示せ。ただし,全ての定数はそのインピーダンスで表すものとする。
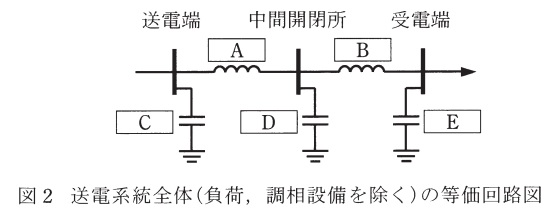
(2) 受電端の負荷が有効電力\( \ 800 \ \mathrm {[MW]} \ \),無効電力\( \ 600 \ \mathrm {[Mvar]} \ \)(遅れ)であるとし,送電端の電圧を\( \ 1.03 \ \mathrm {[p.u.]} \ \),中間開閉所の電圧を\( \ 1.02 \ \mathrm {[p.u.]} \ \),受電端の電圧を\( \ 1.00 \ \mathrm {[p.u.]} \ \)とする場合に必要な中間開閉所と受電端の調相設備の容量\( \ \mathrm {[MV\cdot A]} \ \)(基準電圧における皮相電力値)をそれぞれ求めよ。
【ワンポイント解説】
1種になると送電線のインピーダンスを考慮した\( \ \pi \ \)形等価回路や\( \ \mathrm {T} \ \)形等価回路の問題が出題されます。考え方はそれほど難しい問題にはなりませんが,(2)の計算量が多く,時間が非常にかかる問題です。他の問題で対応できるならば,できるだけ選択したくない問題と言えるでしょう。
1.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路
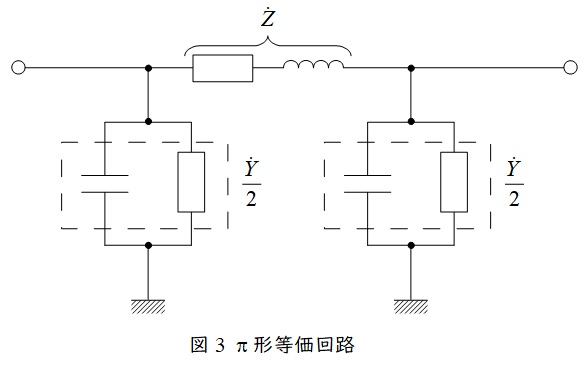
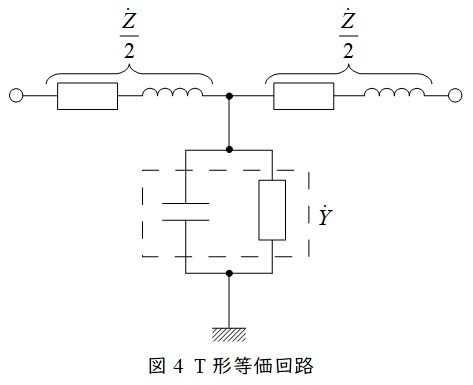
送電線のこう長が大きくなると送電線のリアクタンスや静電容量が無視できなくなるので,\( \ \pi \ \)形等価回路や\( \ \mathrm {T} \ \)形等価回路を適用します。送電線のインピーダンスを\( \ \dot Z \ \),アドミタンスを\( \ \dot Y \ \)とすると,\( \ \pi \ \)形等価回路は図3,\( \ \mathrm {T} \ \)形等価回路は図4のようになります。
電験では送電線の抵抗分やサセプタンス分は無視し,送電線のインダクタンスを\( \ L \ \mathrm {[H]} \ \),静電容量を\( \ C \ \mathrm {[F]} \ \)として,
\[
\begin{eqnarray}
{\dot Z}&=&\mathrm {j}\omega L \\[ 5pt ]
{\dot Y}&=&\mathrm {j}\omega C \\[ 5pt ]
\end{eqnarray}
\]
として扱う問題がほとんどです。
【解答】
(1)\( \ 1 \ \)回線\( \ 1 \ \)区間を\( \ \pi \ \)形等価回路で,単位法で表した定数と送電系統全体の等価回路図を図2としたとき空白\( \ \mathrm {A~E} \ \)に当てはまる単位法で表した定数
題意に沿って送電線\( \ 1 \ \)回線\( \ 1 \ \)区間を\( \ \pi \ \)形等価回路にすると図5のようになる。

図5において,各値はワンポイント解説「1.\( \ \pi \ \)形等価回路と\( \ \mathrm {T} \ \)形等価回路」より,
\[
\begin{eqnarray}
{\dot Z}&=&\mathrm {j}\omega L \\[ 5pt ]
&=&\mathrm {j}2\pi f L \\[ 5pt ]
&=&\mathrm {j}2\times 3.14 \times 50 \times 0.8 \times 10^{-3}\times 100 \\[ 5pt ]
&=&\mathrm {j}25.12 \ \mathrm {[\Omega ]} \\[ 5pt ]
\frac {\dot Y}{2}&=&\frac {\mathrm {j}\omega C}{2} \\[ 5pt ]
&=&\frac {\mathrm {j}2\pi f C}{2} \\[ 5pt ]
&=&\mathrm {j}\pi f C \\[ 5pt ]
&=&\mathrm {j}3.14 \times 50 \times 0.01 \times 10^{-6}\times 100 \\[ 5pt ]
&=&\mathrm {j}1.57 \times 10^{-4} \ \mathrm {[S]} \\[ 5pt ]
\end{eqnarray}
\]
となり,コンデンサのインピーダンス\( \ {\dot Z}_{\mathrm {C}} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {C}}&=&\frac {1}{\mathrm {j}1.57 \times 10^{-4}} \\[ 5pt ]
&≒&-\mathrm {j}6369.4 \ \mathrm {[\Omega ]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,各インピーダンスを単位法で表すと,
\[
\begin{eqnarray}
{\dot Z} \ \mathrm {[p.u.]}&=&\dot Z\times \frac {P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}} \\[ 5pt ]
&=&\mathrm {j}25.12\times \frac {1000\times 10^{6}}{\left( 500\times 10^{3}\right) ^{2}} \\[ 5pt ]
&=&\mathrm {j}0.10048 → \mathrm {j}0.100 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot Z}_{\mathrm {C}} \ \mathrm {[p.u.]}&=&{\dot Z}_{\mathrm {C}}\times \frac {P_{\mathrm {B}}}{V_{\mathrm {B}}^{2}} \\[ 5pt ]
&=&-\mathrm {j}6369.4\times \frac {1000\times 10^{6}}{\left( 500\times 10^{3}\right) ^{2}} \\[ 5pt ]
&=&-\mathrm {j}25.478 → -\mathrm {j}25.5 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ 1 \ \)回線\( \ 1 \ \)区間の\( \ \pi \ \)形等価回路は図6のようになる。
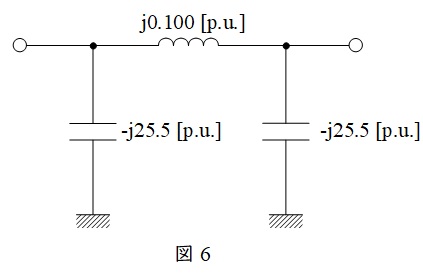
次に図6を図1の送電線に適用すると,図7のようになる。
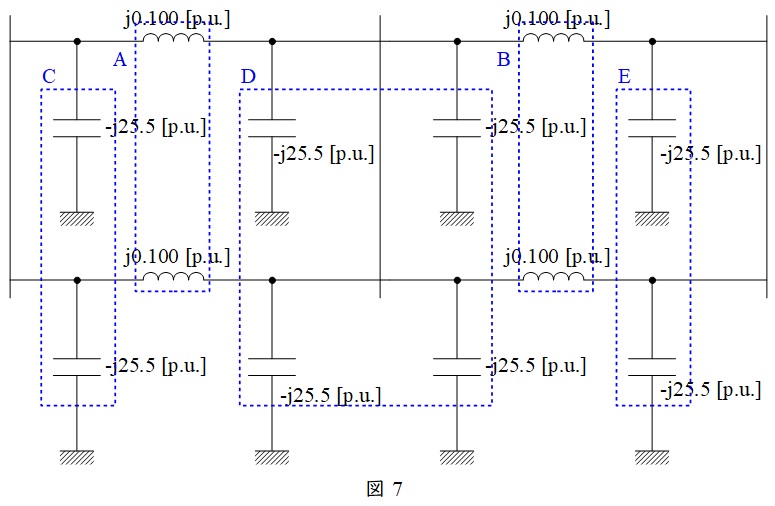
図7において,\( \ \mathrm {A~E} \ \)はそれぞれ,リアクトルとコンデンサの並列回路であるから,
\[
\begin{eqnarray}
\mathrm {A}=\mathrm {B}&=&\frac {\dot Z}{2} \\[ 5pt ]
&=&\frac {\mathrm {j}0.10048}{2} \\[ 5pt ]
&=&\mathrm {j}0.05024 → \mathrm {j}0.0502 \ \mathrm {[p.u.]} \\[ 5pt ]
\mathrm {C}=\mathrm {E}&=&\frac {{\dot Z}_{\mathrm {C}}}{2} \\[ 5pt ]
&=&\frac {-\mathrm {j}25.478}{2} \\[ 5pt ]
&=&-\mathrm {j}12.739 → -\mathrm {j}12.7 \ \mathrm {[p.u.]} \\[ 5pt ]
\mathrm {D}&=&\frac {{\dot Z}_{\mathrm {C}}}{4} \\[ 5pt ]
&=&\frac {-\mathrm {j}25.478}{4} \\[ 5pt ]
&=&-\mathrm {j}6.3695 → -\mathrm {j}6.37 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)題意を満たす場合に必要な中間開閉所と受電端の調相設備の容量
受電端の負荷が有効電力\( \ 800 \ \mathrm {[MW]} \ \),無効電力\( \ 600 \ \mathrm {[Mvar]} \ \)(遅れ)であるから,遅れ無効電力を正として単位法で表すと,
\[
\begin{eqnarray}
P+\mathrm {j}Q&=&0.8+\mathrm {j}0.6 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。これより,負荷電流\( \ {\dot I}_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {L}}&=&\frac {\overline {P+\mathrm {j}Q}}{\overline V_{\mathrm {R}}} \\[ 5pt ]
&=&\frac {0.8-\mathrm {j}0.6}{1.00} \\[ 5pt ]
&=&0.8-\mathrm {j}0.6 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。各電圧電流をまとめ,図8のようにおく。
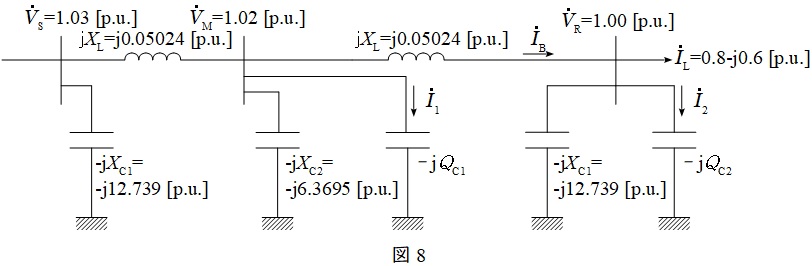
図8より,中間開閉所の電圧\( \ {\dot V}_{\mathrm {M}} \ \)と受電端の電圧\( \ {\dot V}_{\mathrm {R}} \ \)の関係から,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {M}}&=&{\dot V}_{\mathrm {R}}+\mathrm {j}X_{\mathrm {L}}\left( {\dot I}_{\mathrm {L}}+{\dot I}_{2}+\frac {{\dot V}_{\mathrm {R}}}{-\mathrm {j}X_{\mathrm {C1}}}\right) \\[ 5pt ]
&=&1.00+\mathrm {j}0.05024 \times \left( 0.8-\mathrm {j}0.6+{\dot I}_{2}+\frac {1}{-\mathrm {j}12.739}\right) \\[ 5pt ]
&=&1.00+\mathrm {j}0.05024 \times \left( 0.8-\mathrm {j}0.52150+{\dot I}_{2}\right) \\[ 5pt ]
&≒&1.00+\mathrm {j}0.040192+0.026200 +\mathrm {j}0.05024{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ {\dot I}_{2}=\mathrm {j}I_{2} \)とおけるので,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {M}}&≒&\left( 1.0262-0.05024 I_{2}\right) +\mathrm {j}0.040192 \\[ 5pt ]
\end{eqnarray}
\]
となるので,両辺絶対値をとって2乗すると,
\[
\begin{eqnarray}
1.02^{2}&=&\left( 1.0262-0.05024 I_{2}\right) ^{2}+0.040192^{2} \\[ 5pt ]
0.0025241I_{2}^{2}-0.10311I_{2}+0.014302&=&0 \\[ 5pt ]
I_{2}^{2}-40.850I_{2}+5.6662&=&0 \\[ 5pt ]
I_{2}&=&20.425±\sqrt {20.425^{2}-5.6662} \\[ 5pt ]
&≒&0.13908,40.711(不適) \\[ 5pt ]
\end{eqnarray}
\]
となる。基準電流\( \ I_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {B}}&=&\frac {P_{\mathrm {B}}}{\sqrt {3}V_{\mathrm {B}}} \\[ 5pt ]
&=&\frac {1000\times 10^{6}}{\sqrt {3}\times 500\times 10^{3}} \\[ 5pt ]
&≒&1154.7 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
I_{2} \ \mathrm {[A]}&=&I_{2} \ \mathrm {[p.u.]}\times I_{\mathrm {B}} \\[ 5pt ]
&=&0.13908\times 1154.7 \\[ 5pt ]
&≒&160.60 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,受電端の調相設備の容量\( \ Q_{\mathrm {C2}} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {C2}}&=&\sqrt {3}V_{\mathrm {R}}I_{2} \\[ 5pt ]
&=&\sqrt {3}\times 500\times 10^{3}\times 160.60 \\[ 5pt ]
&≒&139080000 \ \mathrm {[V\cdot A]} → 139 \ \mathrm {[MV\cdot A]}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。
次に,\( \ {\dot V}_{\mathrm {M}} \ \)は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {M}}&=&\left( 1.0262-0.05024 I_{2}\right) +\mathrm {j}0.040192 \\[ 5pt ]
&=&\left( 1.0262-0.05024 \times 0.13908\right) +\mathrm {j}0.040192 \\[ 5pt ]
&≒&1.0192 +\mathrm {j}0.040192 \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ {\dot I}_{\mathrm {B}} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {B}}&=&{\dot I}_{\mathrm {L}}+{\dot I}_{2}+\frac {{\dot V}_{\mathrm {R}}}{-\mathrm {j}X_{\mathrm {C1}}} \\[ 5pt ]
&=& 0.8-\mathrm {j}0.6+\mathrm {j}0.13908+\frac {1}{-\mathrm {j}12.739} \\[ 5pt ]
&≒&0.8 -\mathrm {j}0.38242 \\[ 5pt ]
\end{eqnarray}
\]
であるから,送電端の電圧\( \ {\dot V}_{\mathrm {S}} \ \)と中間開閉所の電圧\( \ {\dot V}_{\mathrm {M}} \ \)の関係から,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {S}}&=&{\dot V}_{\mathrm {M}}+\mathrm {j}X_{\mathrm {L}}\left( {\dot I}_{\mathrm {B}}+{\dot I}_{1}+\frac {{\dot V}_{\mathrm {M}}}{-\mathrm {j}X_{\mathrm {C2}}}\right) \\[ 5pt ]
&=&1.0192 +\mathrm {j}0.040192+\mathrm {j}0.05024 \times \left( 0.8 -\mathrm {j}0.38242+{\dot I}_{1}+\frac {1.0192 +\mathrm {j}0.040192}{-\mathrm {j}6.3695}\right) \\[ 5pt ]
&=&1.0192 +\mathrm {j}0.040192+\mathrm {j}0.05024 \times \left( 0.8 -\mathrm {j}0.38242+{\dot I}_{1}+\mathrm {j}0.16001-0.0063101\right) \\[ 5pt ]
&=&1.0192 +\mathrm {j}0.040192+\mathrm {j}0.05024 \times \left( 0.79369 -\mathrm {j}0.22241+{\dot I}_{1}\right) \\[ 5pt ]
&=&1.0192 +\mathrm {j}0.040192+\mathrm {j}0.039875 +0.011174+\mathrm {j}0.05024{\dot I}_{1} \\[ 5pt ]
&=&1.0304 +\mathrm {j}0.080067+\mathrm {j}0.05024{\dot I}_{1} \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ {\dot I}_{1} \)は\( \ {\dot V}_{\mathrm {M}} \ \)より\( \ 90° \ \)進んでいるので,
\[
\begin{eqnarray}
{\dot I}_{1}&=&\left( -0.040192 +\mathrm {j}1.0192\right) I_{1} \\[ 5pt ]
\end{eqnarray}
\]
とおくことができるので,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {S}}&=&1.0304 +\mathrm {j}0.080067+\mathrm {j}0.05024\times \left( -0.040192 +\mathrm {j}1.0192\right) I_{1} \\[ 5pt ]
&≒&1.0304 -0.050205I_{1}+\mathrm {j}0.080067-\mathrm {j}0.0020192I_{1} \\[ 5pt ]
\end{eqnarray}
\]
となり,両辺絶対値をとって2乗すると,
\[
\begin{eqnarray}
1.03^{2}&=&\left( 1.0304 -0.050205I_{1}\right) ^{2}+\left( 0.080067-0.0020192I_{1}\right) ^{2} \\[ 5pt ]
0.0025246I_{1}^{2}-0.10379I_{1}+0.0072349&=&0 \\[ 5pt ]
I_{1}^{2}-41.111I_{1}+2.8658&=&0 \\[ 5pt ]
I_{1}&=&20.5555±\sqrt {20.5555^{2}-2.8658} \\[ 5pt ]
&≒&0.069437,41.041(不適) \\[ 5pt ]
\end{eqnarray}
\]
なる。よって,
\[
\begin{eqnarray}
I_{1} \ \mathrm {[A]}&=&I_{1} \ \mathrm {[p.u.]}\times I_{\mathrm {B}} \\[ 5pt ]
&=&0.069437\times 1154.7 \\[ 5pt ]
&≒&80.179 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となり,基準電圧を流したときの電流\( \ I_{1}^{\prime } \ \)は,
\[
\begin{eqnarray}
I_{1}^{\prime }&=&\frac {1.00}{1.02}I_{1} \\[ 5pt ]
&=&\frac {1.00}{1.02}\times 80.179 \\[ 5pt ]
&≒&78.607 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,中間開閉所の調相設備の容量\( \ Q_{\mathrm {C1}} \ \)は,
\[
\begin{eqnarray}
Q_{\mathrm {C1}}&=&\sqrt {3}V_{\mathrm {M}}I_{1} ^{\prime }\\[ 5pt ]
&=&\sqrt {3}\times 500\times 10^{3}\times 78.607 \\[ 5pt ]
&≒&68076000 \ \mathrm {[V\cdot A]} → 68.1 \ \mathrm {[MV\cdot A]}\\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん