【問題】
【難易度】★★☆☆☆(やや易しい)
送電線保護装置の信頼度による供給支障確率について,次の問に答えなさい。
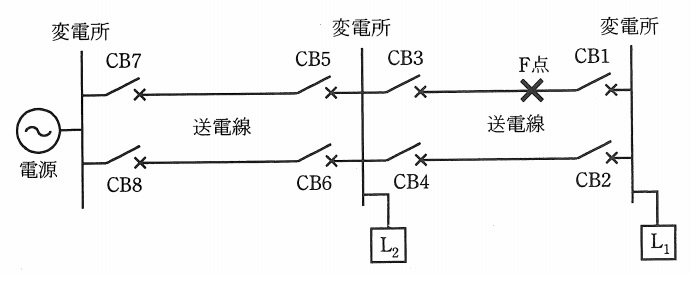
\( \ 2 \ \)回線送電線で負荷\( \ \mathrm {L_{1}} \ \)と負荷\( \ \mathrm {L_{2}} \ \)へ供給している図の電力系統において,各変電所の送電線引出し遮断器\( \ \mathrm {CB1~CB8} \ \)には,送電線の主保護リレー(当該送電線のみを保護範囲とする。)と後備保護リレー(事故電流が流れる方向に当該送電線から二区間隣の送電線までを保護範囲とする。)が設置されている。この系統のいずれかの送電線に\( \ 1 \ \)回線事故が発生した場合,正常であれば事故区間の両端の遮断器が主保護リレー動作で遮断し,事故送電線のみが停電して変電所の供給支障は生じない。しかし,保護リレーや動作回路等の不具合で遮断器が誤不動作した場合,誤不動作遮断器よりも事故電流源側の遮断器が,後備保護リレー動作により遮断するため,変電所が供給支障となる。
主保護リレー動作の遮断器及び後備保護リレー動作の遮断器が誤不動作する確率がいずれも\( \ 0.01 \ \)であり,いずれの遮断器も誤動作で遮断する確率は\( \ 0 \ \)であるとする。
いま,送電線の\( \ \mathrm {F} \ \)点で事故が生じた場合,供給支障が生じない確率,負荷\( \ \mathrm {L_{1}} \ \)のみが供給支障となる確率,及び負荷\( \ \mathrm {L_{1}} \ \)と負荷\( \ \mathrm {L_{2}} \ \)両方が供給支障となる確率をそれぞれ求めなさい。なお,負荷が停電したときは,再閉路成功・失敗いずれの場合でも供給支障とする。答の数値は,小数点以下第\( \ 4 \ \)位まで求めること。
ただし,各変電所に母線保護リレーは設置されておらず,保護リレー及び検出,動作回路は各遮断器に個別に独立して設置されており,他の保護リレーからの影響は受けないものとし,後備保護リレー相互間の時限等の協調は十分図られているものとする。また,\( \ \mathrm {CB7} \ \)又は\( \ \mathrm {CB8} \ \)が誤不動作した場合には,電源の保護リレーが動作して電源が停電するものとする。
【ワンポイント解説】
計算自体は非常に易しい問題です。\( \ \mathrm {F} \ \)点が事故の場合,主保護が\( \ \mathrm {CB1}\)と\( \ \mathrm {CB3} \ \)で,後備保護が\( \ \mathrm {CB4} \ \),\( \ \mathrm {CB7} \ \),\( \ \mathrm {CB8} \ \)となります。あとはすべてのパターンについて各遮断器がどう動作した場合に\( \ \mathrm {L_{1}} \ \),\( \ \mathrm {L_{2}} \ \)が供給支障となるかを考え確率を出せば,ミスも防げると思います。
【解答】
\( \ \mathrm {F} \ \)点で事故が発生した場合に動作するのは,主保護が\( \ \mathrm {CB1} \ \)と\( \ \mathrm {CB3} \ \),後備保護が\( \ \mathrm {CB4} \ \),\( \ \mathrm {CB7} \ \)と\( \ \mathrm {CB8} \ \)である。以下のパターンが考えられる。
①\( \ \mathrm {CB1} \ \)動作,\( \ \mathrm {CB3} \ \)動作 → 供給支障なし
②\( \ \mathrm {CB1} \ \)不動作,\( \ \mathrm {CB3} \ \)動作 → \( \ \mathrm {CB4} \ \)動作 →\( \ \mathrm {L_{1}} \ \)供給支障
③\( \ \mathrm {CB1} \ \)不動作,\( \ \mathrm {CB3} \ \)動作 → \( \ \mathrm {CB4} \ \)不動作 → \( \ \mathrm {CB7} \ \)動作,\( \ \mathrm {CB8} \ \)動作 → \( \ \mathrm {L_{1}} \ \),\( \ \mathrm {L_{2}} \ \)供給支障
④\( \ \mathrm {CB1} \ \)不動作,\( \ \mathrm {CB3} \ \)動作 → \( \ \mathrm {CB4} \ \)不動作 → \( \ \mathrm {CB7} \ \)不動作もしくは\( \ \mathrm {CB8} \ \)不動作 → 電源停止 → \( \ \mathrm {L_{1}} \ \),\( \ \mathrm {L_{2}} \ \)供給支障
⑤\( \ \mathrm {CB1} \ \)動作,\( \ \mathrm {CB3} \ \)不動作 → \( \ \mathrm {CB7} \ \)動作,\( \ \mathrm {CB8} \ \)動作 → \( \ \mathrm {L_{1}} \ \),\( \ \mathrm {L_{2}} \ \)供給支障
⑥\( \ \mathrm {CB1} \ \)動作,\( \ \mathrm {CB3} \ \)不動作 → \( \ \mathrm {CB7} \ \)不動作もしくは\( \ \mathrm {CB8} \ \)不動作 → 電源停止 → \( \ \mathrm {L_{1}} \ \),\( \ \mathrm {L_{2}} \ \)供給支障
⑦\( \ \mathrm {CB1} \ \)不動作,\( \ \mathrm {CB3} \ \)不動作 → \( \ \mathrm {CB7} \ \)動作,\( \ \mathrm {CB8} \ \)動作 → \( \ \mathrm {L_{1}} \ \),\( \ \mathrm {L_{2}} \ \)供給支障
⑧\( \ \mathrm {CB1} \ \)不動作,\( \ \mathrm {CB3} \ \)不動作 → \( \ \mathrm {CB7} \ \)不動作もしくは\( \ \mathrm {CB8} \ \)不動作 → 電源停止 → \( \ \mathrm {L_{1}} \ \),\( \ \mathrm {L_{2}} \ \)供給支障
(1)供給支障が生じない確率
供給支障を生じない確率は上記①の時である。したがって,\( \ \mathrm {CB1} \ \)動作と\( \ \mathrm {CB3} \ \)動作がともに動作する確率は,
\[
\begin{eqnarray}
\left( 1-0.01 \right)\times \left( 1-0.01 \right)&=&0.9801 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\(\mathrm {L_{1}}\)のみが供給支障となる確率
\(\mathrm {L_{1}}\)のみが供給支障となる確率は上記②の時である。したがって,その確率は,
\[
\begin{eqnarray}
0.01 \times \left( 1-0.01 \right) \times \left( 1-0.01 \right)≒0.0098 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\(\mathrm {L_{1}}\),\(\mathrm {L_{2}}\)両方が供給支障となる確率
\(\mathrm {L_{1}}\),\(\mathrm {L_{2}}\)両方が供給支障となる確率は,①,②以外のすべてのケースである。したがって,
\[
\begin{eqnarray}
1-0.9801-0.0098&=&0.0101 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(参考)③~⑧のパターンの確率
③\(\mathrm {CB1}\)不動作,\(\mathrm {CB3}\)動作 → \(\mathrm {CB4}\)不動作 → \(\mathrm {CB7}\)動作,\(\mathrm {CB8}\)動作 → \(\mathrm {L_{1}}\),\(\mathrm {L_{2}}\)供給支障
\[
\begin{eqnarray}
0.01 \times \left( 1-0.01 \right) \times 0.01 \times \left( 1-0.01 \right) \times \left( 1-0.01 \right) &≒& 0.0001 \\[ 5pt ]
\end{eqnarray}
\]
④\(\mathrm {CB1}\)不動作,\(\mathrm {CB3}\)動作 → \(\mathrm {CB4}\)不動作 → \(\mathrm {CB7}\)不動作もしくは\(\mathrm {CB8}\)不動作 → 電源停止 → \(\mathrm {L_{1}}\),\(\mathrm {L_{2}}\)供給支障
\[
\begin{eqnarray}
0.01 \times \left( 1-0.01 \right) \times 0.01 \times \left\{ 1- \left( 1-0.01 \right) \times \left( 1-0.01 \right) \right\} &≒& 1.79 \times 10^{-6} ≒0.0000 \\[ 5pt ]
\end{eqnarray}
\]
⑤\(\mathrm {CB1}\)動作,\(\mathrm {CB3}\)不動作 → \(\mathrm {CB7}\)動作,\(\mathrm {CB8}\)動作 → \(\mathrm {L_{1}}\),\(\mathrm {L_{2}}\)供給支障
\[
\begin{eqnarray}
\left( 1-0.01 \right) \times 0.01 \times \left( 1-0.01 \right) \times \left( 1-0.01 \right) &≒& 0.0097 \\[ 5pt ]
\end{eqnarray}
\]
⑥\(\mathrm {CB1}\)動作,\(\mathrm {CB3}\)不動作 → \(\mathrm {CB7}\)不動作もしくは\(\mathrm {CB8}\)不動作 → 電源停止 → \(\mathrm {L_{1}}\),\(\mathrm {L_{2}}\)供給支障
\[
\begin{eqnarray}
\left( 1-0.01 \right) \times 0.01 \times \left\{ 1- \left( 1-0.01 \right) \times \left( 1-0.01 \right) \right\} &≒& 0.0002 \\[ 5pt ]
\end{eqnarray}
\]
⑦\(\mathrm {CB1}\)不動作,\(\mathrm {CB3}\)不動作 → \(\mathrm {CB7}\)動作,\(\mathrm {CB8}\)動作 → \(\mathrm {L_{1}}\),\(\mathrm {L_{2}}\)供給支障
\[
\begin{eqnarray}
0.01 \times 0.01 \times \left( 1-0.01 \right) \times \left( 1-0.01 \right) &≒&0.0001 \\[ 5pt ]
\end{eqnarray}
\]
⑧\(\mathrm {CB1}\)不動作,\(\mathrm {CB3}\)不動作 → \(\mathrm {CB7}\)不動作もしくは\(\mathrm {CB8}\)不動作 → 電源停止 → \(\mathrm {L_{1}}\),\(\mathrm {L_{2}}\)供給支障
\[
\begin{eqnarray}
0.01 \times 0.01 \times \left\{ 1- \left( 1-0.01 \right) \times \left( 1-0.01 \right) \right\} &≒&0.0000 \\[ 5pt ]
\end{eqnarray}
\]
③~⑧の合計は,
\[
\begin{eqnarray}
0.0001+0.0000+0.0097+0.0002+0.0001+0.0000&=&0.0101 \\[ 5pt ]
\end{eqnarray}
\]
となり,(3)の答えと合致する。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん