【問題】
【難易度】★★★☆☆(普通)
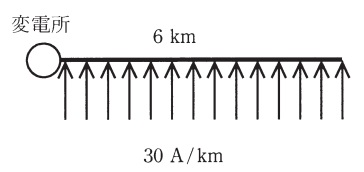
図に示すように,こう長\( \ 6 \ \mathrm {km} \ \),電圧\( \ 6.6 \ \mathrm {kV} \ \)の三相3線式配電線があり,需要家の分散型電源が平等かつ連続的に分布して電力を供給しているものとする。この配電線の1地点にコンデンサを接続して,配電線損失電力を減らすことを考える。このとき,次の問に答えよ。ただし,分散型電源は,電流密度が\( \ 30 \ \mathrm {A / km} \ \),分散型電源側からみて進み力率\( \ 95 \ \mathrm {%} \ \)の定電流源とする。また,配電線各地点の電圧位相の差は無視できるものとする。
(1) 変電所より\( \ 4 \ \mathrm {km} \ \)の地点にコンデンサを接続する。接続前後における抵抗損による配電線損失電力をそれぞれ\(L_{1}\),\(L_{2}\)とするとき,\(L_{1}-L_{2}=L \ \mathrm {[kW]}\)を求めよ。ただし,コンデンサは電流\(I_{\mathrm {C}} \ \mathrm {[A]}\)の定電流源,配電線の抵抗は\(1\)相あたり\(\ r \ \mathrm {[\Omega / km]}\)とする。
(2) 上記(1)の\(L\)を最大とするコンデンサ容量\(Q_{\mathrm {C}} \ \mathrm {[kvar]}\)を求めよ。ただし,コンデンサの接続点における配電線電圧は\( \ 6.6 \ \mathrm {kV} \ \)とする。
【ワンポイント解説】
二種でもよく出題される平等負荷での配電線での電力損失の計算と似ている問題です。電力損失の差は無効電力の差のみであることに気づけばそれほど難しい計算ではないと思います。もちろん有効電力を考慮しても解くことは可能です。
【解答】
(1)コンデンサ接続前後における抵抗損による配電線損失電力の差
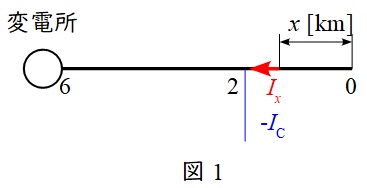
配電線末端を基準として,各部の電流等を図1の通りとする。接続前後における抵抗損による配電線損失電力の差は無効電力分のみであるから,無効電流のみを考慮する。
無効電流の電流密度\(i_{\mathrm {q}}\)は力率が\(0.95\)であるから,
\[
\begin{eqnarray}
i_{\mathrm {q}} &=&30\times \sqrt {1-0.95^{2}} \\[ 5pt ]
&≒&9.3675 \ \mathrm {[A / km]} \\[ 5pt ]
\end{eqnarray}
\]
となる。コンデンサ接続前,配電線末端から距離\(x \ \mathrm {[km]}\)の地点での無効電流の大きさ\(I_{\mathrm {qx}}\)は,
\[
\begin{eqnarray}
I_{\mathrm {qx}} &=&9.3675x \\[ 5pt ]
\end{eqnarray}
\]
であるから,無効電流による配電線損失電力\(L_{\mathrm {1q}}\)は,
\[
\begin{eqnarray}
L_{\mathrm {1q}} &=&\int ^{6}_{0} 3r{I_{\mathrm {qx}}}^{2} \mathrm {d}x \times 10^{-3} \\[ 5pt ]
&=&9.3675^{2}r\int ^{6}_{0} 3x^{2} \mathrm {d}x \times 10^{-3} \\[ 5pt ]
&≒&87.750r\left[ x^{3}\right] ^{6}_{0} \times 10^{-3} \\[ 5pt ]
&=&18.954r \\[ 5pt ]
\end{eqnarray}
\]
と求められる。次にコンデンサ接続後,\(x≦2\)までの無効電流は変わらないが\(2<x≦6\)において,無効電流の大きさ\(I_{\mathrm {qx}}\)は,
\[
\begin{eqnarray}
I_{\mathrm {qx}} &=&9.3675x-I_{\mathrm {C}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,コンデンサ接続後の無効電流による配電線損失電力\(L_{\mathrm {2q}}\)は,
\[
\begin{eqnarray}
L_{\mathrm {2q}} &=&\int ^{6}_{0} 3r{I_{\mathrm {qx}}}^{2} \mathrm {d}x \times 10^{-3} \\[ 5pt ]
&=&\int ^{2}_{0} 3r\times \left( 9.3675x\right) ^{2} \mathrm {d}x \times 10^{-3}+\int ^{6}_{2} 3r\times \left( 9.3675x-I_{\mathrm {C}} \right) ^{2} \mathrm {d}x \times 10^{-3} \\[ 5pt ]
&≒&87.750r\int ^{2}_{0} 3x^{2} \mathrm {d}x \times 10^{-3} +3r\int ^{6}_{2} \left( 87.750x^{2}-2\times 9.3675I_{\mathrm {C}}x+{I_{\mathrm {C}}}^{2}\right) \mathrm {d}x \times 10^{-3} \\[ 5pt ]
&=&87.750r\int ^{6}_{0} 3x^{2} \mathrm {d}x \times 10^{-3} -3r\times 9.3675I_{\mathrm {C}}\int ^{6}_{2} 2x \mathrm {d}x\times 10^{-3} + 3r{I_{\mathrm {C}}}^{2} \int ^{6}_{2} 1 \mathrm {d}x \times 10^{-3} \\[ 5pt ]
&=&\left( 87.750r\left[ x^{3}\right] ^{6}_{0} -3r\times 9.3675I_{\mathrm {C}}\left[ x^{2}\right] ^{6}_{2} + 3r{I_{\mathrm {C}}}^{2} \left[ x\right] ^{6}_{2}\right) \times 10^{-3} \\[ 5pt ]
&=&18.954r-0.89928rI_{\mathrm {C}}+0.012r{I_{\mathrm {C}}}^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,コンデンサ接続前後における抵抗損による配電線損失電力の差\(L\)は,
\[
\begin{eqnarray}
L &=&L_{1}-L_{2} \\[ 5pt ]
&=&L_{\mathrm {1q}}-L_{\mathrm {2q}} \\[ 5pt ]
&=&18.954r-\left( 18.954r-0.89928rI_{\mathrm {C}}+0.012r{I_{\mathrm {C}}}^{2}\right) \\[ 5pt ]
&=&0.89928rI_{\mathrm {C}}-0.012r{I_{\mathrm {C}}}^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\(L\)を最大とするコンデンサ容量\(Q_{\mathrm {C}} \ \mathrm {[kvar]}\)
\(L\)を最大にするためには,\(\displaystyle \frac {\mathrm {d}L}{\mathrm {d}I_{\mathrm {C}}}=0\)にすればよいので,
\[
\begin{eqnarray}
\frac {\mathrm {d}L}{\mathrm {d}I_{\mathrm {C}}} =0.89928r-0.024rI_{\mathrm {C}} &=&0 \\[ 5pt ]
I_{\mathrm {C}}&=&37.47 \mathrm {[A]}\\[ 5pt ]
\end{eqnarray}
\]
となる。よって,コンデンサ容量\(Q_{\mathrm {C}} \ \mathrm {[kvar]}\)は,接続点における配電線電圧\(V_{\mathrm {C}}=6.6 \ \mathrm {[kV]}\)であるので,
\[
\begin{eqnarray}
Q_{\mathrm {C}} &=&\sqrt {3} V_{\mathrm {C}}I_{\mathrm {C}} \\[ 5pt ]
&=&\sqrt {3} \times 6.6\times 37.47 \\[ 5pt ]
&≒&428.34 → 428 \ \mathrm {[kvar]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん