【問題】
【難易度】★★★★★(難しい)
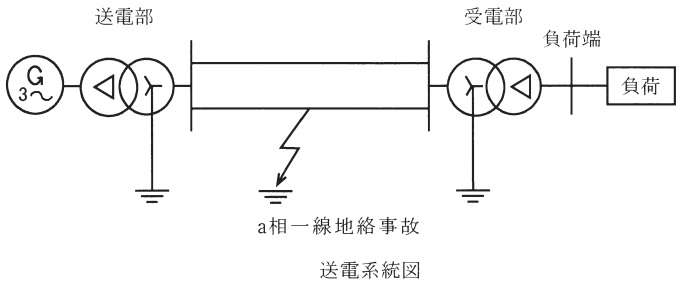
図に示すように,送電線両端の変圧器の中性点が直接接地されている,こう長\( \ 200 \ \mathrm {[km]} \ \)の\( \ 500 \ \mathrm {[kV]} \ \)並行\( \ 2 \ \)回線送電線を考える。この送電線の中間地点において,片方の回線に\( \ \mathrm {a} \ \)相一線地絡事故が発生した。なお,地絡インピーダンスは\( \ 0 \ \mathrm {[p.u.]} \ \)とし,送電系統の各構成機器の定数は次の値とする。また,単位法における基準値は,電圧\( \ 500 \ \mathrm {[kV]} \ \),容量\( \ 1 \ 000 \ \mathrm {[MV\cdot A]} \ \)を用いる。
・送電線正相及び逆相リアクタンス(\( \ 1 \ \)回線当たり):\( \ 0.1 \ \mathrm {[p.u. / 100 km ]} \ \)
・送電線零相リアクタンス(\( \ 1 \ \)回線当たり):\( \ 0.3 \ \mathrm {[p.u. / 100 km ]} \ \)
・送電部,受電部の変圧器漏れリアクタンス:\( \ 0.1 \ \mathrm {[p.u.]} \ \)
・発電機リアクタンス:正相\( \ 0.05 \ \mathrm {[p.u.]} \ \),逆相\( \ 0.02 \ \mathrm {[p.u.]} \ \),零相\( \ 0.01 \ \mathrm {[p.u.]} \ \)
・負荷:負荷端電圧\( \ 1.0 \ \mathrm {[p.u.]} \ \)のとき,遅れ力率\( \ 0.9 \ \)で皮相電力\( \ 0.5 \ \mathrm {[p.u.]} \ \)をとる三相平衡の定インピーダンス負荷
また,送電系統の抵抗成分,静電容量成分,回線間の相互誘導は無視する。このとき,次の問に答えよ。ただし,(5)の解答の精度を保つため,(1)から(3)の解答は有効数字\( \ 4 \ \)桁で示せ。
(1) 事故前は負荷端の電圧の大きさが\( \ 1.0 \ \mathrm {[p.u.]} \ \)で運用されている。このときの発電機の正相リアクタンス背後電圧の大きさ及び送電線の中間地点の電圧の大きさを\( \ \mathrm {p.u.} \ \)値で求めよ。なお,変圧器の巻数比はすべて基準状態(\( \ \mathrm {p.u.} \ \)にて\( \ 1 : 1 \ \))とする。
(2) 送電線の事故点からみた,対称座標法における,送電系統の正相,逆相,零相回路をそのインピーダンス値を含めて示せ。
(3) (2)で求めた,正相,逆相,零相回路を鳳・テブナンの等価回路で表せ。
(4) 図に示すように,片方の回線の中間地点で\( \ \mathrm {a} \ \)相一線地絡事故が発生したとき,その状態を表す正相,逆相,零相回路を接続した図をその理由と共に示せ。
(5) \( \ \mathrm {a} \ \)相一線地絡事故点における地絡電流\( \ \mathrm {[kA]} \ \)を計算せよ。
【ワンポイント解説】
対称座標法を利用した\( \ 1 \ \)線地絡故障計算に関する問題です。
電験においては,対称座標法はメカニズムを理解するというよりも,解き方を暗記することが重要な内容です。
電験\( \ 1 \ \)種では様々なパターンの問題が出題されているので,問題を解きながら少しずつ習得していって下さい。
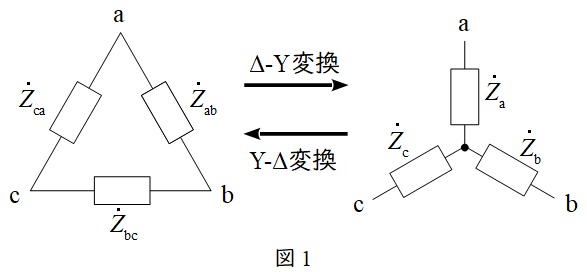
1.不平衡負荷の\( \ \mathrm {\Delta – Y} \ \)変換と\( \ \mathrm {Y – \Delta} \ \)変換
a.\( \ \mathrm {\Delta – Y} \ \)変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {a}} &=& \frac {{\dot Z}_{\mathrm {ab}}{\dot Z}_{\mathrm {ca}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {b}} &=& \frac {{\dot Z}_{\mathrm {bc}}{\dot Z}_{\mathrm {ab}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
{\dot Z}_{\mathrm {c}} &=& \frac {{\dot Z}_{\mathrm {ca}}{\dot Z}_{\mathrm {bc}}}{{\dot Z}_{\mathrm {ab}}+{\dot Z}_{\mathrm {bc}}+{\dot Z}_{\mathrm {ca}}} \\[ 5pt ]
\end{eqnarray}
\]
b.\( \ \mathrm {Y – \Delta} \ \)変換
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {ab}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {c}}} \\[ 5pt ]
{\dot Z}_{\mathrm {bc}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {a}}} \\[ 5pt ]
{\dot Z}_{\mathrm {ca}} &=& \frac {{\dot Z}_{\mathrm {a}}{\dot Z}_{\mathrm {b}}+{\dot Z}_{\mathrm {b}}{\dot Z}_{\mathrm {c}}+{\dot Z}_{\mathrm {c}}{\dot Z}_{\mathrm {a}}}{{\dot Z}_{\mathrm {b}}} \\[ 5pt ]
\end{eqnarray}
\]
2.対称座標法
故障計算をする際に,非常に便利な方法で,以下のように対称座標変換されます。
零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2}
\end{eqnarray}
\]
零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-Z_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-Z_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-Z_{2}{\dot I}_{2}
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)事故前の発電機の正相リアクタンス背後電圧の大きさ及び送電線の中間地点の電圧の大きさ(\( \ \mathrm {p.u.} \ \)値)
三相平衡している条件では,事故発生前は正相回路のみ考えれば良い。
送電線の\( \ 1 \ \)回線当たりの正相リアクタンス\( \ X_{\mathrm {l1}} \ \mathrm {[p.u.]} \ \)は,こう長が\( \ 200 \ \mathrm {[km]} \ \)であるため,
\[
\begin{eqnarray}
X_{\mathrm {l1}} &=&2\times 0.1 \\[ 5pt ]
&=&0.2 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であり,発電機の正相リアクタンス\( \ X_{\mathrm {G1}}=0.05 \ \mathrm {[p.u.]} \ \),変圧器の漏れリアクタンス\( \ X_{\mathrm {T}}=0.1 \ \mathrm {[p.u.]} \ \),負荷端の電圧\( \ V_{\mathrm {L}}=1.0 \ \mathrm {[p.u.]} \ \)となるので,事故前の等価回路は図2のようになる。
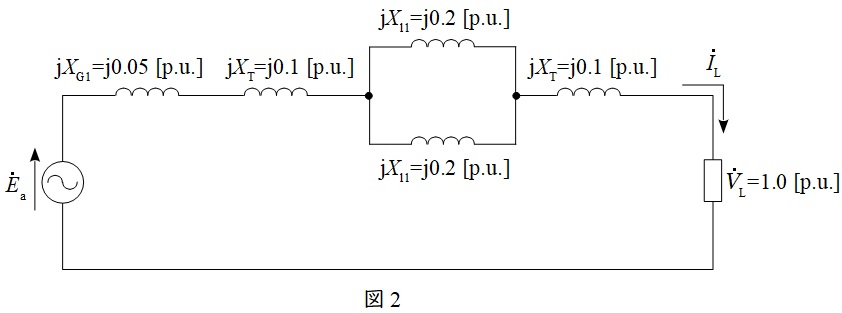
図2において,負荷は負荷端電圧\( \ V_{\mathrm {L}}=1.0 \ \mathrm {[p.u.]} \ \)のとき,遅れ力率\( \ \cos \theta =0.9 \ \)で皮相電力\( \ S=0.5 \ \mathrm {[p.u.]} \ \)をとる三相平衡の定インピーダンス負荷なので,負荷電流\( \ {\dot I}_{\mathrm {L}} \ \mathrm {[p.u.]} \ \)は,遅れを正とすると,
\[
\begin{eqnarray}
\dot S &=&{\dot V}_{\mathrm {L}}\overline {{\dot I}_{\mathrm {L}}} \\[ 5pt ]
{\dot I}_{\mathrm {L}} &=&\frac {\overline {\dot S}}{\overline {{\dot V}_{\mathrm {L}}}} \\[ 5pt ]
&=&\frac {S\left( \cos \theta -\mathrm {j}\sin \theta \right) }{V_{\mathrm {L}}} \\[ 5pt ]
&=&\frac {S\left( \cos \theta -\mathrm {j}\sqrt {1-\cos ^{2}\theta } \right) }{V_{\mathrm {L}}} \\[ 5pt ]
&=&\frac {0.5 \times \left( 0.9 -\mathrm {j}\sqrt {1-0.9 ^{2} } \right) }{1.0} \\[ 5pt ]
&≒&0.45-\mathrm {j}0.217945 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,正相リアクタンス背後電圧\( \ {\dot E}_{\mathrm {a}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {a}} &=&{\dot V}_{\mathrm {L}}+\mathrm {j}\left( X_{\mathrm {T}}+\frac {X_{\mathrm {l1}}}{2}+X_{\mathrm {T}}+X_{\mathrm {G1}}\right) {\dot I}_{\mathrm {L}} \\[ 5pt ]
&=&1.0+\mathrm {j}\left( 0.1+\frac {0.2}{2}+0.1+0.05\right) \times \left( 0.45-\mathrm {j}0.217945\right) \\[ 5pt ]
&=&1.0+\mathrm {j}0.35 \times \left( 0.45-\mathrm {j}0.217945\right) \\[ 5pt ]
&≒&1.07628+\mathrm {j}0.1575 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさは,
\[
\begin{eqnarray}
\left| {\dot E}_{\mathrm {a}}\right| &=&\sqrt {1.07628^{2}+0.1575^{2}} \\[ 5pt ]
&≒&1.08774 → 1.088 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
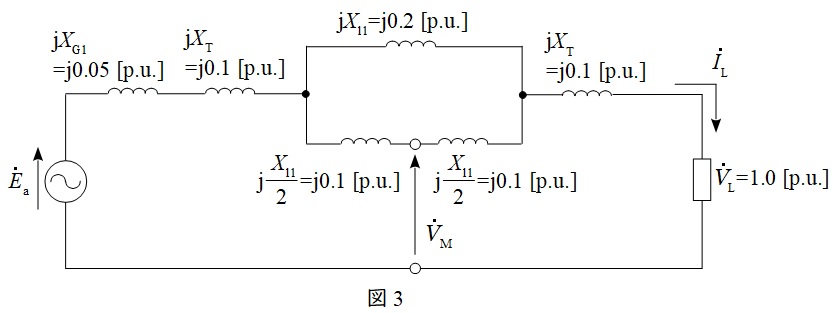
次に,中間地点の電圧\( \ {\dot V}_{\mathrm {M}} \ \mathrm {[p.u.]} \ \)は,図3に示す電圧であるので,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {M}} &=&{\dot V}_{\mathrm {L}}+\mathrm {j} X_{\mathrm {T}}{\dot I}_{\mathrm {L}}+ \mathrm {j} \frac {X_{\mathrm {l1}}}{2}\cdot \frac {{\dot I}_{\mathrm {L}}}{2} \\[ 5pt ]
&=&{\dot V}_{\mathrm {L}}+\mathrm {j} \left( X_{\mathrm {T}}+\frac {X_{\mathrm {l1}}}{4}\right) {\dot I}_{\mathrm {L}} \\[ 5pt ]
&=&1.0+\mathrm {j}\left( 0.1+\frac {0.2}{4}\right) \times \left( 0.45-\mathrm {j}0.217945\right) \\[ 5pt ]
&=&1.0+\mathrm {j}0.15 \times \left( 0.45-\mathrm {j}0.217945\right) \\[ 5pt ]
&≒&1.03269+\mathrm {j}0.0675 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となり,その大きさは,
\[
\begin{eqnarray}
\left| {\dot V}_{\mathrm {M}}\right| &=&\sqrt {1.03269^{2}+0.0675^{2}} \\[ 5pt ]
&≒&1.03489 → 1.035 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)対称座標法における,送電系統の正相,逆相,零相回路をそのインピーダンス値を含めて示す
負荷のインピーダンス\( \ {\dot Z}_{\mathrm {L}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {L}} &=&\frac {{\dot V}_{\mathrm {L}}}{{\dot I}_{\mathrm {L}}} \\[ 5pt ]
&=&\frac {1.0}{0.45-\mathrm {j}0.217945} \\[ 5pt ]
&=&\frac {1.0}{0.45-\mathrm {j}0.217945}\times \frac {0.45+\mathrm {j}0.217945}{0.45+\mathrm {j}0.217945} \\[ 5pt ] \\[ 5pt ]
&=& \frac {0.45+\mathrm {j}0.217945}{0.25000} \\[ 5pt ]
&=&1.80+\mathrm {j}0.87178 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,正相回路は図3-1のようになる。
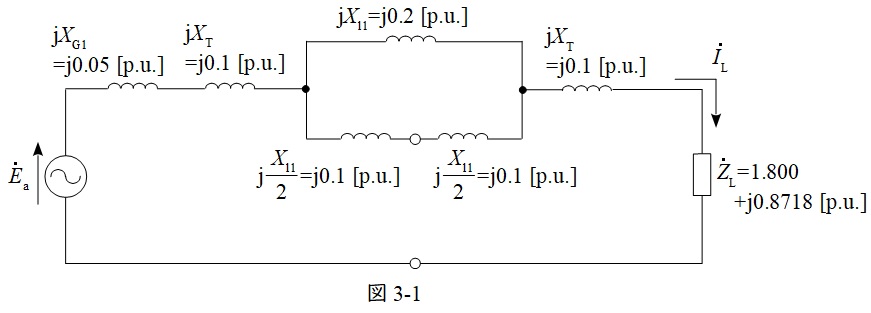
逆相回路及び零相回路においても正相回路と同様に求めると,図4及び図5のようになる。
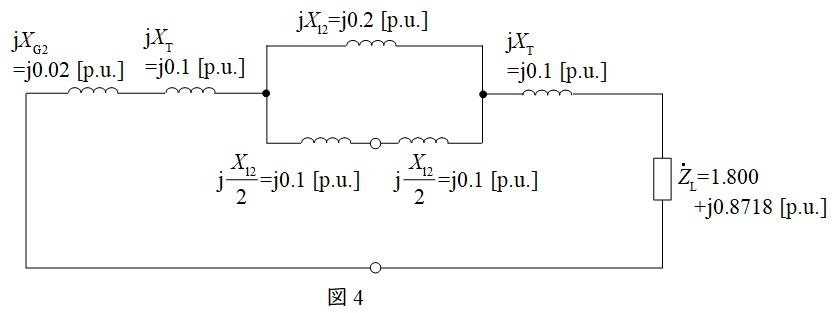
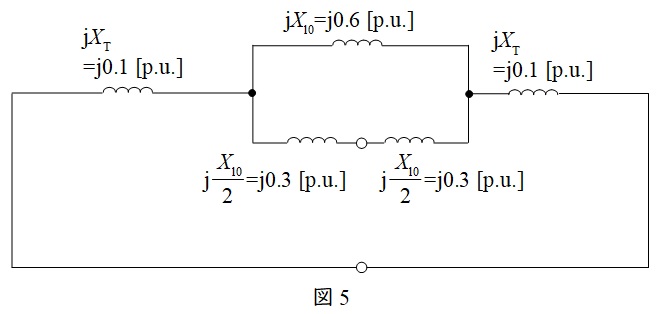
(3)(2)で求めた,正相,逆相,零相回路を鳳・テブナンの等価回路で表す
図3-1の送電線部を\( \ \mathrm {\Delta – Y} \ \)変換すると図3-2のようになり,それぞれのリアクタンスの大きさ\( \ X_{\mathrm {l1}}^{\prime } \ \mathrm {[p.u.]} \ \)及び\( \ X_{\mathrm {l1}}^{\prime \prime } \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
X_{\mathrm {l1}}^{\prime } &=&\frac {\displaystyle X_{\mathrm {l1}}\cdot \frac {X_{\mathrm {l1}}}{2}}{\displaystyle X_{\mathrm {l1}}+\frac {X_{\mathrm {l1}}}{2}+\frac {X_{\mathrm {l1}}}{2}} \\[ 5pt ]
&=&\frac {\displaystyle 0.2\times 0.1}{\displaystyle 0.2+0.1+0.1} \\[ 5pt ]
&=&0.05 \ \mathrm {[p.u.]} \\[ 5pt ]
X_{\mathrm {l1}}^{\prime \prime } &=&\frac {\displaystyle \frac {X_{\mathrm {l1}}}{2}\cdot \frac {X_{\mathrm {l1}}}{2}}{\displaystyle X_{\mathrm {l1}}+\frac {X_{\mathrm {l1}}}{2}+\frac {X_{\mathrm {l1}}}{2}} \\[ 5pt ]
&=&\frac {\displaystyle 0.1\times 0.1}{\displaystyle 0.2+0.1+0.1} \\[ 5pt ]
&=&0.025 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。
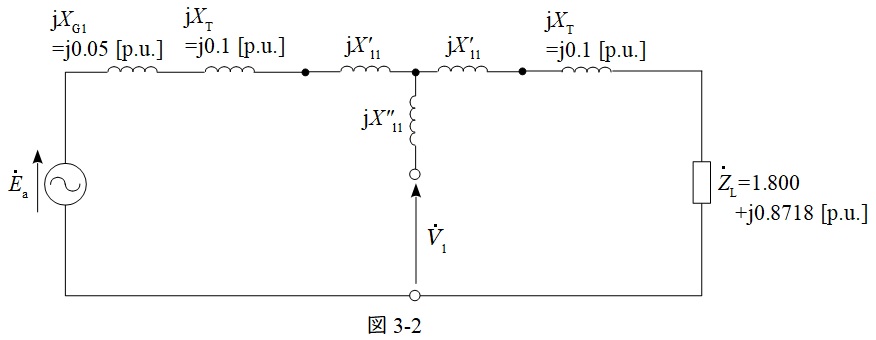
逆相回路及び零相回路についても同様に示すと,図4-1及び図5-1のようになる。


よって,図3-2,図4-1,図5-1において鳳・テブナンの定理を適用するため,事故点からみたインピーダンス\( \ {\dot Z}_{\mathrm {1}} \ \mathrm {[p.u.]} \ \),\( \ {\dot Z}_{\mathrm {2}} \ \mathrm {[p.u.]} \ \),\( \ {\dot Z}_{\mathrm {0}} \ \mathrm {[p.u.]} \ \)をそれぞれ求めると,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {1}} &=&\mathrm {j}X_{\mathrm {l1}}^{\prime \prime }+\frac {1}{\displaystyle \frac {1}{\mathrm {j}X_{\mathrm {G1}}+\mathrm {j}X_{\mathrm {T}}+\mathrm {j}X_{\mathrm {l1}}^{\prime }}+\displaystyle \frac {1}{{\dot Z}_{\mathrm {L}}+\mathrm {j}X_{\mathrm {T}}+\mathrm {j}X_{\mathrm {l1}}^{\prime }}} \\[ 5pt ]
&=&\mathrm {j}0.025+\frac {1}{\displaystyle \frac {1}{\mathrm {j}0.05+\mathrm {j}0.1+\mathrm {j}0.05}+\displaystyle \frac {1}{1.80+\mathrm {j}0.87178+\mathrm {j}0.1+\mathrm {j}0.05}} \\[ 5pt ]
&=&\mathrm {j}0.025+\frac {1}{-\mathrm {j}5+\displaystyle \frac {1}{1.80+\mathrm {j}1.02178}} \\[ 5pt ]
&=&\mathrm {j}0.025+\frac {1}{-\mathrm {j}5+\displaystyle \frac {1.80-\mathrm {j}1.02178}{1.80^{2}+1.02178^{2}}} \\[ 5pt ]
&≒&\mathrm {j}0.025+\frac {1}{-\mathrm {j}5+0.420165-\mathrm {j}0.238509} \\[ 5pt ]
&≒&\mathrm {j}0.025+\frac {1}{0.420165-\mathrm {j}5.23851} \\[ 5pt ]
&=&\mathrm {j}0.025+\frac {0.420165+\mathrm {j}5.23851}{0.420165^{2}+5.23851^{2}} \\[ 5pt ]
&≒&\mathrm {j}0.025+0.0152669+\mathrm {j}0.189674 \\[ 5pt ]
&≒&0.0152669+\mathrm {j}0.214674 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot Z}_{\mathrm {2}} &=&\mathrm {j}X_{\mathrm {l2}}^{\prime \prime }+\frac {1}{\displaystyle \frac {1}{\mathrm {j}X_{\mathrm {G2}}+\mathrm {j}X_{\mathrm {T}}+\mathrm {j}X_{\mathrm {l2}}^{\prime }}+\displaystyle \frac {1}{{\dot Z}_{\mathrm {L}}+\mathrm {j}X_{\mathrm {T}}+\mathrm {j}X_{\mathrm {l2}}^{\prime }}} \\[ 5pt ]
&=&\mathrm {j}0.025+\frac {1}{\displaystyle \frac {1}{\mathrm {j}0.02+\mathrm {j}0.1+\mathrm {j}0.05}+\displaystyle \frac {1}{1.80+\mathrm {j}0.87178+\mathrm {j}0.1+\mathrm {j}0.05}} \\[ 5pt ]
&≒&\mathrm {j}0.025+\frac {1}{-\mathrm {j}5.88235+0.420165-\mathrm {j}0.238509} \\[ 5pt ]
&≒&\mathrm {j}0.025+\frac {1}{0.420165-\mathrm {j}6.12086} \\[ 5pt ]
&=&\mathrm {j}0.025+\frac {0.420165+\mathrm {j}6.12086}{0.420165^{2}+6.12086^{2}} \\[ 5pt ]
&≒&\mathrm {j}0.025+0.0111623+\mathrm {j}0.162610 \\[ 5pt ]
&≒&0.0111623+\mathrm {j}0.187610 \ \mathrm {[p.u.]} \\[ 5pt ]
{\dot Z}_{\mathrm {0}} &=&\mathrm {j}X_{\mathrm {l0}}^{\prime \prime }+\frac {1}{\displaystyle \frac {1}{\mathrm {j}X_{\mathrm {T}}+\mathrm {j}X_{\mathrm {l0}}^{\prime }}+\displaystyle \frac {1}{\mathrm {j}X_{\mathrm {T}}+\mathrm {j}X_{\mathrm {l0}}^{\prime }}} \\[ 5pt ]
&=&\mathrm {j}0.075+\frac {1}{\displaystyle \frac {1}{\mathrm {j}0.1+\mathrm {j}0.15}+\displaystyle \frac {1}{\mathrm {j}0.1+\mathrm {j}0.15}} \\[ 5pt ]
&=&\mathrm {j}0.075+\frac {1}{-\mathrm {j}8} \\[ 5pt ]
&=&\mathrm {j}0.075+\mathrm {j}0.125 \\[ 5pt ]
&=&\mathrm {j}0.200 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。以上から,鳳・テブナンの等価回路は図6のようになる

(4)片方の回線の中間地点で\( \ \mathrm {a} \ \)相一線地絡事故が発生したとき,その状態を表す正相,逆相,零相回路を接続した図をその理由と共に示す
\( \ \mathrm {a} \ \)相一線地絡事故が発生すると,ワンポイント解説「2.対称座標法」で定義する電圧・電流において,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2}=0 &・・・・・・ ①& \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}=0 &・・・・・・ ②& \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2}=0 &・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
が成立する。②,③より,
\[
\begin{eqnarray}
{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
a^{2}{\dot I}_{1} + a{\dot I}_{2} &=& a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\left( a^{2}-a \right) {\dot I}_{1}&=&\left( a^{2}-a \right) {\dot I}_{2} \\[ 5pt ]
{\dot I}_{1}&=& {\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2}&=&0 \\[ 5pt ]
{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{1}&=&0 \\[ 5pt ]
{\dot I}_{0}+ \left( a^{2}+a \right) {\dot I}_{1}&=&0 \\[ 5pt ]
{\dot I}_{0}- {\dot I}_{1}&=&0 \\[ 5pt ]
{\dot I}_{0} &=&{\dot I}_{1} \\[ 5pt ]
\end{eqnarray}
\]
となる。さらに,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
&=&3{\dot I}_{0} \\[ 5pt ]
\end{eqnarray}
\]
が成立するので,対称座標法の関係式を満たす回路は図7のようになる。
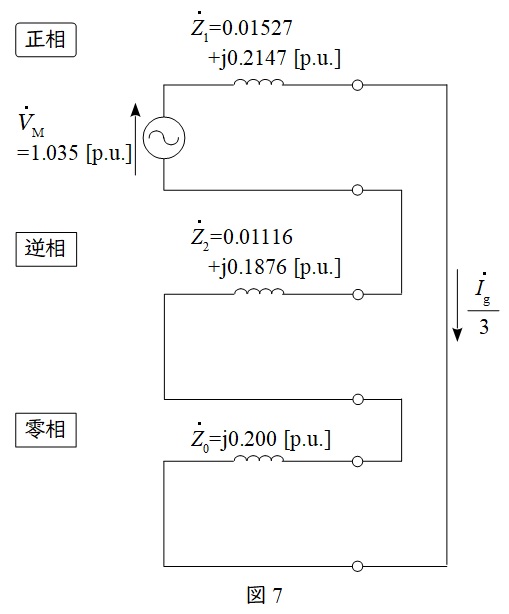
(5)\( \ \mathrm {a} \ \)相一線地絡事故点における地絡電流\( \ \mathrm {[kA]} \ \)
図7について回路方程式を立てると,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {M}} &=&\left( {\dot Z}_{\mathrm {1}}+{\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {0}}\right) \frac {{\dot I}_{\mathrm {g}}}{3} \\[ 5pt ]
{\dot I}_{\mathrm {g}} &=&\frac {3{\dot V}_{\mathrm {M}}}{ {\dot Z}_{\mathrm {1}}+{\dot Z}_{\mathrm {2}}+{\dot Z}_{\mathrm {0}}} \\[ 5pt ]
&=&\frac {3\times \left( 1.03269+\mathrm {j}0.0675\right) }{ 0.0152669+\mathrm {j}0.214674+0.0111623+\mathrm {j}0.187610+\mathrm {j}0.200} \\[ 5pt ]
&=&\frac {3.09807+\mathrm {j}0.2025}{ 0.0264292+\mathrm {j}0.602284} \\[ 5pt ]
\end{eqnarray}
\]
となるため,地絡電流の大きさ\( \ I_{\mathrm {g}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {g}} &=&\sqrt {\frac {3.09807^{2}+0.2025^{2}}{ 0.0264292^{2}+0.602284^{2}}} \\[ 5pt ]
&≒&5.14989 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。基準電流\( \ I_{\mathrm {n}} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {n}} &=&\frac {P_{\mathrm {n}}}{\sqrt {3}V_{\mathrm {n}}} \\[ 5pt ]
&=&\frac {1000\times 10^{6}}{\sqrt {3}\times 500\times 10^{3}} \\[ 5pt ]
&≒&1154.70 \ \mathrm {[A]} \\[ 5pt ]
\end{eqnarray}
\]
であるため,
\[
\begin{eqnarray}
I_{\mathrm {g}} &=&5.14989\times 1154.70 \\[ 5pt ]
&≒&5946.6 \ \mathrm {[A]} → 5.95 \ \mathrm {[kA]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん