【問題】
【難易度】★★★★☆(やや難しい)
コンデンサ形計器用変圧器(\(\mathrm {CVT}\))に関して,次の問に答えよ。
(1) 図は\( \ \mathrm {CVT} \ \)の基本回路である。端子\( \ \mathrm {a-b} \ \)から左側の部分を一つの電圧源と一つのコンデンサを用いて等価回路に書き直すとどうなるか,端子\( \ \mathrm {a-b} \ \)から右側の部分を接続した形で具体的に描け。
(2) 図において,二次負担\( \ z \ \)の如何にかかわらず常にコンデンサ\( \ C_{1} \ \)と\( \ C_{2} \ \)の静電容量の逆比で系統電圧が分圧されて補助\( \ \mathrm {VT} \ \)(図の\( \ \mathrm {Tr} \ \))に入力されるための条件を,(1)で得た等価回路に基づいて導出せよ。ただし,系統周波数を\( \ f \ \)とする。
(3) 簡単のため,以下では二次負担\( \ z \ \)は非接続,補助\( \ \mathrm {VT} \ \)(図の\( \ \mathrm {Tr} \ \))の励磁インダクタンスを\( \ L_{\mathrm {m}} \ \)とし,漏れインダクタンスは無視する。(1)で得た等価回路の\( \ L \ \)と\( \ \mathrm {Tr} \ \)を一つのインダクタンスにまとめた等価回路に書き直せ。
(4) 無電圧から時刻\( \ t=0 \ \)にて急に系統電圧\( \ v(t)=V\sin \ \omega t \ (\omega =2\pi f)\)が図のように印加されたときの過渡応答を考えたい。(1)で得た等価回路のコンデンサ電圧\( \ v_{\mathrm {c}}(t) \ \)についての微分方程式を書け。
(5) \( \ L \ \)の初期電流とコンデンサの初期電荷はなく,補助\( \ \mathrm {VT} \ \)と\( \ L \ \)は線形範囲で動作するものとして(4)で得た微分方程式を解いて\( \ v_{\mathrm {c}}(t) \ \)を時刻\( \ t \ \)の関数の式として示せ。(ヒント:線形微分方程式の解は,その定常解に,右辺(強制入力)が零の場合の解(過渡解)を加えた形で表せる。)
(6) 実際には磁気的非線形性のため鉄共振が発生し,等価コンデンサ電圧\( \ v_{\mathrm {c}}(t) \ \)に低周波数の電圧成分が生じる場合がある。小問(1)と(5)の結果と飽和時に\( \ L_{\mathrm {m}} \ \)が低下することを用いて,大きな低周波数電圧成分が\( \ \mathrm {Tr} \ \)二次側に生じる理由を定性的に説明せよ。
【ワンポイント解説】
前半の(1)~(4)は二種レベルの問題で比較的短時間で解けるので,時間がなく部分点狙いであれば良い問題であると思います。(5)の微分方程式でリアクトルとコンデンサを含む微分方程式なので,やや時間がかかりそうだ\(\cdots \)と予想し,他の問題を先に解いてから戻ってきても良いと思います。
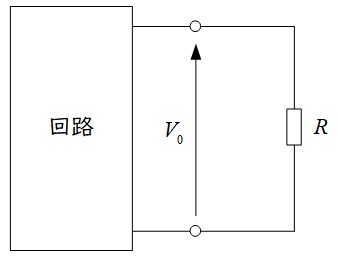
1.テブナンの定理
下図において回路中の2端子の開放電圧を\( \ V_{0} \ \),電圧源を短絡し,電流源を開放した時の端子から見た合成抵抗を\( \ R_{0} \ \)とした時,外部抵抗\( \ R \ \)とした時,抵抗\( \ R \ \)を流れる電流\( \ I \ \)は,下式の通りとなります。
\[
\begin{eqnarray}
I&=&\frac {V_{0}}{R+R_{0}} \\[ 5pt ]
\end{eqnarray}
\]
※コンデンサでも同様にインピーダンスとして計算することが可能です。
【関連する「電気の神髄」記事】
【解答】
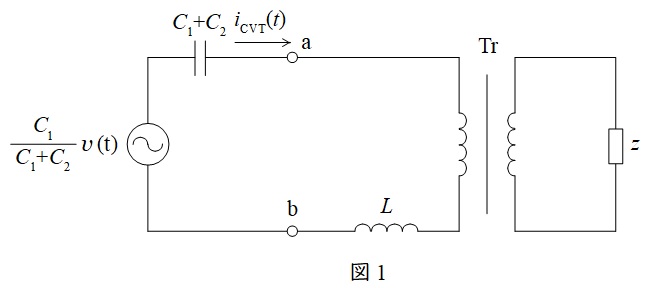
(1)端子\( \ \mathrm {a-b} \ \)から左側の部分を一つの電圧源と一つのコンデンサを用いて等価回路を書く
\( \ \mathrm {a-b} \ \)の右側部分を切り離した場合,\( \ \mathrm {a-b} \ \)間にかかる電圧\( \ V_{0} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
V_{0}&=&\frac {C_{1}}{C_{1}+C_{2}}v(t) \\[ 5pt ]
\end{eqnarray}
\]
であり,電圧源を短絡した時の\( \ \mathrm {a-b} \ \)から見た合成静電容量\( \ C_{0} \ \)は,
\[
\begin{eqnarray}
C_{0}&=&C_{1}+C_{2} \\[ 5pt ]
\end{eqnarray}
\]
であるから,等価回路は図1のようになる。
(2)常にコンデンサ\( \ C_{1} \ \)と\( \ C_{2} \ \)の静電容量の逆比で系統電圧が分圧されて補助\( \ \mathrm {VT} \ \)(図の\( \ \mathrm {Tr} \ \))に入力されるための条件
\( \ C_{1} \ \)と\( \ C_{2} \ \)の静電容量の逆比で系統電圧が分圧されて\( \ \mathrm {Tr} \ \)に入力するということは,図1の等価回路において,電源電圧\( \ V_{0} \ \)がそのまま\( \ \mathrm {Tr} \ \)に入力するということになる。したがって,この条件において,\( \ C_{1} \ \)と\( \ C_{2} \ \)と\( \ L \ \)の合成インピーダンスが零とならなければならない。したがって,
\[
\begin{eqnarray}
\mathrm {j}2\pi f L+\frac {1}{\mathrm {j}2\pi f\left( C_{1}+C_{2}\right) }&=&0 \\[ 5pt ]
\mathrm {j}2\pi f L-\mathrm {j}\frac {1}{2\pi f\left( C_{1}+C_{2}\right) }&=&0 \\[ 5pt ]
2\pi f L-\frac {1}{2\pi f\left( C_{1}+C_{2}\right) }&=&0 \\[ 5pt ]
2\pi f L&=&\frac {1}{2\pi f\left( C_{1}+C_{2}\right) } \\[ 5pt ]
4\pi ^{2}f^{2} L\left( C_{1}+C_{2}\right) &=&1 \\[ 5pt ]
\end{eqnarray}
\]
となれば良い。
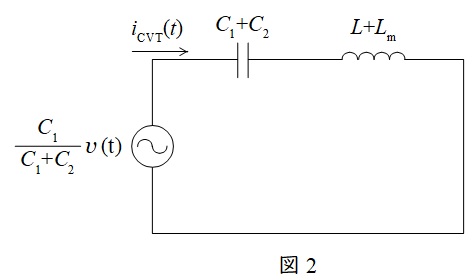
(3)(1)で得た等価回路の\( \ L \ \)と\( \ \mathrm {Tr} \ \)を一つのインダクタンスにまとめた等価回路を書く
二次側の\( \ z \ \)を非接続,漏れインダクタンスは無視することができるので,等価回路は図2のようになる。
(4)等価回路のコンデンサ電圧\( \ v_{\mathrm {c}}(t) \ \)についての微分方程式
図2において,回路方程式は,
\[
\begin{eqnarray}
v_{\mathrm {c}}(t)+\left( L+L_{\mathrm {m}}\right) \frac {\mathrm {d}i_{\mathrm {CVT}}}{\mathrm {d}t}&=&\frac {C_{1}}{C_{1}+C_{2}}v(t) \\[ 5pt ]
v_{\mathrm {c}}(t)+\left( L+L_{\mathrm {m}}\right) \frac {\mathrm {d}^{2}q_{\mathrm {CVT}}}{\mathrm {d}t^{2}}&=&\frac {C_{1}}{C_{1}+C_{2}}v(t) \\[ 5pt ]
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
q_{\mathrm {CVT}}&=&\left( C_{1}+C_{2}\right) v_{\mathrm {c}}(t) \\[ 5pt ]
\end{eqnarray}
\]
であるから,
\[
\begin{eqnarray}
v_{\mathrm {c}}(t)+\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) \frac {\mathrm {d}^{2}v_{\mathrm {c}}}{\mathrm {d}t^{2}}&=&\frac {C_{1}}{C_{1}+C_{2}}v(t) \\[ 5pt ]
\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) \frac {\mathrm {d}^{2}v_{\mathrm {c}}}{\mathrm {d}t^{2}}+v_{\mathrm {c}}(t)&=&\frac {C_{1}}{C_{1}+C_{2}}V\sin \omega t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)微分方程式を解いて\( \ v_{\mathrm {c}}(t) \ \)を時刻\( \ t \ \)の関数の式として示す
過渡解を\( \ v_{\mathrm {ct}}(t) \ \),定常解を\( \ v_{\mathrm {cs}}(t) \ \)と置く。定常解は\(\displaystyle v_{\mathrm {cs}}(t) =AV\sin \omega t \ \)とおくと,
\[
\begin{eqnarray}
-\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) A\omega ^{2}V\sin \omega t+AV\sin \omega t&=&\frac {C_{1}}{C_{1}+C_{2}}V\sin \omega t \\[ 5pt ]
-\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) A\omega ^{2}+A&=&\frac {C_{1}}{C_{1}+C_{2}} \\[ 5pt ]
A&=&\frac {C_{1}}{\left( C_{1}+C_{2}\right) \left\{ 1-\omega ^{2}\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) \right\} } \\[ 5pt ]
\end{eqnarray}
\]
となり,(2)より,\( \ \displaystyle \omega^{2}\left( C_{1}+C_{2}\right) =\frac {1}{L} \ \)であるから,
\[
\begin{eqnarray}
A&=&\frac {C_{1}}{\left( C_{1}+C_{2}\right) \left( 1-\displaystyle \frac {L+L_{\mathrm {m}}}{L} \right) } \\[ 5pt ]
&=&-\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,定常解は,
\[
\begin{eqnarray}
v_{\mathrm {cs}}(t) &=&-\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\sin \omega t \\[ 5pt ]
\end{eqnarray}
\]
と求められる。一方,過渡解は\(\displaystyle v_{\mathrm {ct}}(t) =B\mathrm {e}^{\beta t} \ \)と置き,微分方程式の右辺を零とすると,
\[
\begin{eqnarray}
\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) \beta ^{2}B\mathrm {e}^{\beta t}+B\mathrm {e}^{\beta t}&=&0 \\[ 5pt ]
\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) \beta ^{2}+1&=&0 \\[ 5pt ]
\beta &=&±\mathrm {j}\frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,過渡解は
\[
\begin{eqnarray}
v_{\mathrm {ct}}(t) &=&B_{1}\mathrm {e}^{\mathrm {j}\frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t} +B_{2}\mathrm {e}^{-\mathrm {j}\frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t} \\[ 5pt ]
&=&B_{1}\left\{ \cos \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t+\mathrm {j}\sin \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t\right\} \\[ 5pt ]
&&+B_{2}\left\{ \cos \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t-\mathrm {j}\sin \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t\right\} \\[ 5pt ]
&=&B_{3}\cos \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t+B_{4}\sin \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t \\[ 5pt ]
\end{eqnarray}
\]
となる。(ただし,\( \ B_{3}=B_{1}+B_{2} \ \),\( \ B_{4}=\mathrm {j} \left( B_{1}-B_{2}\right) \ \)とした。)
したがって,一般解は,
\[
\begin{eqnarray}
v_{\mathrm {c}}(t) &=&v_{\mathrm {cs}}(t)+v_{\mathrm {ct}}(t) \\[ 5pt ]
&=&-\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\sin \omega t+B_{3}\cos \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t+B_{4}\sin\frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t \\[ 5pt ]
\end{eqnarray}
\]
となる。初期条件\( \ v_{\mathrm {c}}(0) = 0 \ \)より,
\[
\begin{eqnarray}
v_{\mathrm {c}}(0)&=&B_{3} \\[ 5pt ]
B_{3}&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となり,一般解は,
\[
\begin{eqnarray}
v_{\mathrm {c}}(t)&=&-\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\sin \omega t+B_{4}\sin \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t \\[ 5pt ]
\end{eqnarray}
\]
となる。両辺微分すると,
\[
\begin{eqnarray}
\frac {\mathrm {d}v_{\mathrm {c}}}{\mathrm {d}t}&=&-\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\omega \cos \omega t+B_{4}\frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}\cos \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t \\[ 5pt ]
\end{eqnarray}
\]
となり,初期条件\( \displaystyle \ i_{\mathrm {CVT}}(0)=\left( C_{1}+C_{2}\right) \left. \frac {\mathrm {d}v_{\mathrm {c}}(t)}{\mathrm {d}t}\right| _{t=0} =0 \ \)より,
\[
\begin{eqnarray}
0&=&-\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\omega +B_{4}\frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }} \\[ 5pt ]
B_{4}&=&\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }V\omega \\[ 5pt ]
\end{eqnarray}
\]
となるので,求める解は,
\[
\begin{eqnarray}
v_{\mathrm {c}}(t)&=&-\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\sin \omega t+\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }V\omega \sin \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t \\[ 5pt ]
&=&\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\left\{ -\sin \omega t+\omega \sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }\sin \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t\right\} \\[ 5pt ]
\end{eqnarray}
\]
となる。
(6)小問(1)と(5)の結果と飽和時に\( \ L_{\mathrm {m}} \ \)が低下することを用いて,大きな低周波数電圧成分が\( \ \mathrm {Tr} \ \)二次側に生じる理由を定性的に説明
(2)より,\(\displaystyle \omega =\frac {1}{\sqrt {L\left( C_{1}+C_{2}\right) }}\)であるため,これを(5)の解答の過渡成分に代入して整理すると,
\[
\begin{eqnarray}
v_{\mathrm {ct}}(t)&=&\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\left\{ \omega \sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }\sin \frac {1}{\sqrt {\left( L+L_{\mathrm {m}}\right) \left( C_{1}+C_{2}\right) }}t\right\} \\[ 5pt ]
&=&\frac {LC_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}V\left( \sqrt {\frac {L+L_{\mathrm {m}}}{L}} \sin \sqrt {\frac {L}{ L+L_{\mathrm {m}}}}\omega t\right) \\[ 5pt ]
&=&\frac {C_{1}}{\left( C_{1}+C_{2}\right) L_{\mathrm {m}}}\sqrt {L\left( L+L_{\mathrm {m}}\right) }V\sin \sqrt {\frac {L}{ L+L_{\mathrm {m}}}}\omega t \\[ 5pt ]
\end{eqnarray}
\]
となる。この成分は\(\displaystyle \ \sqrt {\frac {L}{ L+L_{\mathrm {m}}}} < 1 \ \)なので低周波成分となる。また,磁気飽和して,\( \ L_{\mathrm {m}} \ \)の値が小さくなると,\( \ v_{\mathrm {ct}}(t) \ \)の値が大きくなり,大きな低周波数電圧成分が発生する。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん