《電力・管理》〈変電〉[R03:問4]２台のタップ付き変圧器の並行運転に関する計算問題

【問題】

【難易度】★★★☆☆（普通）

送電用変電所において二つのタップ付き変圧器\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)が並行運転している。\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)は同一の変圧器で，定格電圧は\( \ 275 / 154 \ \mathrm {kV} \ \)，\( \ 2 \ \)次側換算漏れリアクタンスは\( \ 8.0 \ \mathrm {\Omega } \ \)であり，励磁インピーダンス，巻線抵抗は無視できるものとする。タップは\( \ 1 \ \)次側（高圧側）にあり，中間タップの\( \ 275 \ \mathrm {kV} \ \)から\( \ 1 \ \)段当たり\( \ 3 \ \mathrm {kV} \ \)の間隔で上下に切り替えることができる。タップ段数による\( \ 2 \ \)次側換算漏れリアクタンスの変動はないものとする。変電所\( \ 1 \ \)次側の電圧は\( \ 275 \ \mathrm {kV} \ \)一定である。次の問に答えよ。

(1)　変圧器\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)のタップ段数が共に中間タップであり，\( \ 1 \ \)次側母線から合計で\( \ 280 \ \mathrm {MV\cdot A} \ \)，遅れ力率\( \ 0.8 \ \)の電力を送電しているとき，各変圧器の\( \ 2 \ \)次側に流れる電流値\( \ I_{\mathrm {A}} \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {B}} \ \mathrm {[A]} \ \)を求めよ。

(2)　次に，変圧器\( \ \mathrm {A} \ \)のタップ段数のみを\( \ 3 \ \)段下げて\( \ 2 \ \)次側電圧を高くすると，両変圧器間に循環電流が流れて負荷電流に重畳する。負荷インピーダンスの大きさは変圧器の\( \ 2 \ \)次側換算漏れリアクタンスより十分に大きいとして，次のa)及びb)について答えよ。

a)　循環電流を求めて，各変圧器の\( \ 2 \ \)次側に流れる電流値\( \ I_{\mathrm {A}}^{\prime } \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {B}}^{\prime } \ \mathrm {[A]} \ \)を求めよ。

b)　前問a)の結果を用いて，両変圧器間のタップ段数の差によって生じる二つの変圧器で消費される遅れ無効電力の和の変化\( \ \Delta Q_{\mathrm {L}} \ \mathrm {[Mvar]} \ \)を求めよ。

【ワンポイント解説】

変圧器の循環電流に関する問題です。
公式自体は\( \ 2 \ \)種の頃から扱ってきた公式がほとんどなので，問題の内容をしっかりと理解できれば難解な問題ではなかったかと思います。
循環電流の考え方を本問で理解しておくようにしましょう。

1.変圧器の巻数比と変圧比，変流比の関係
変圧器の一次側の巻数\( \ N_{1} \ \)，電圧\( \ V_{1} \ \mathrm {[V]} \ \)，電流\( \ I_{1} \ \mathrm {[A]} \ \)，二次側の巻数\( \ N_{2} \ \)，電圧\( \ V_{2} \ \mathrm {[V]} \ \)，電流\( \ I_{2} \ \mathrm {[A]} \ \)とすると，それぞれの関係は，
\[
\begin{eqnarray}
\frac {N_{1}}{N_{2}} &=&\frac {V_{1}}{V_{2}}=\frac {I_{2}}{I_{1}} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)各変圧器の\( \ 2 \ \)次側に流れる電流値\( \ I_{\mathrm {A}} \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {B}} \ \mathrm {[A]} \ \)
変圧器\( \ \mathrm {A} \ \)，\( \ \mathrm {B} \ \)共に中間タップであるため，どちらの二次電圧も\( \ V_{\mathrm {A}}=V_{\mathrm {B}}=154 \ \mathrm {[kV]} \ \)であり，負荷分担は\( \ P_{\mathrm {A}}=P_{\mathrm {B}}=140 \ \mathrm {[MV\cdot A]} \ \)となる。したがって，それぞれの負荷に流れる電流\( \ I_{\mathrm {A}} \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {B}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {A}}=I_{\mathrm {B}} &=&\frac {P_{\mathrm {A}}}{\sqrt {3}V_{\mathrm {A}}} \\[ 5pt ] &=&\frac {140\times 10^{6}}{\sqrt {3}\times 154\times 10^{3}} \\[ 5pt ] &≒&524.86　→　525 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)a)循環電流と各変圧器の\( \ 2 \ \)次側に流れる電流値\( \ I_{\mathrm {A}}^{\prime } \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {B}}^{\prime } \ \mathrm {[A]} \ \)
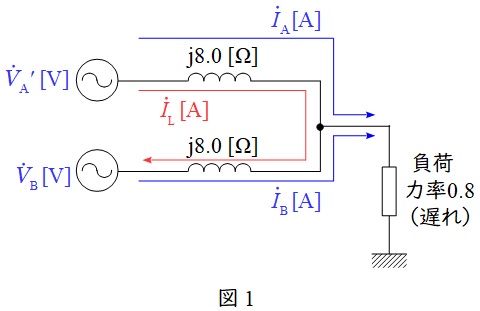
循環電流を\( \ {\dot I}_{\mathrm {L}} \ \mathrm {[A]} \ \)とすると，各電流の流れは図1のようになる。
\( \ 2 \ \)次側電圧を基準とすると，負荷は遅れ力率\( \ 0.8 \ \)であるため，各変圧器に流れる負荷電流\( \ {\dot I}_{\mathrm {A}} \ \mathrm {[A]} \ \)及び\( \ {\dot I}_{\mathrm {B}} \ \mathrm {[A]} \ \)は，(1)より，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {A}}={\dot I}_{\mathrm {B}} &=&I_{\mathrm {A}}\left( \cos \theta -\mathrm {j}\sin \theta \right) \\[ 5pt ] &=&524.86\times \left( 0.8-\mathrm {j}\sqrt {1-0.8^{2}}\right) \\[ 5pt ] &≒&419.89-\mathrm {j}314.92 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] である。また，変圧器\( \ \mathrm {A} \ \)のタップ段数を\( \ 3 \ \)段下げたので，そのときの\( \ 2 \ \)次側電圧\( \ {\dot V}_{\mathrm {A}}^{\prime } \ \mathrm {[kV]} \ \)は，
\[
\begin{eqnarray}
{\dot V}_{\mathrm {A}}^{\prime } &=&\frac {154}{275-3\times 3}\times 275 \\[ 5pt ] &≒&159.21 \ \mathrm {[kV]} \\[ 5pt ] \end{eqnarray}
\] であるから，循環電流\( \ {\dot I}_{\mathrm {L}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {L}} &=&\frac {\displaystyle \frac {{\dot V}_{\mathrm {A}}^{\prime }}{\sqrt {3}}-\frac {{\dot V}_{\mathrm {B}}}{\sqrt {3}}}{\mathrm {j}8.0\times 2} \\[ 5pt ] &=&\frac {\displaystyle \frac {159.21\times 10^{3}}{\sqrt {3}}-\frac {154\times 10^{3}}{\sqrt {3}}}{\mathrm {j}8.0\times 2} \\[ 5pt ] &=&\frac {159.21-154}{\sqrt {3}\times \mathrm {j}8.0\times 2}\times 10^{3} \\[ 5pt ] &≒&-\mathrm {j}188.00 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。したがって，各変圧器の\( \ 2 \ \)次側に流れる電流\( \ {\dot I}_{\mathrm {A}}^{\prime } \ \mathrm {[A]} \ \)，\( \ {\dot I}_{\mathrm {B}}^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {A}}^{\prime } &=&{\dot I}_{\mathrm {A}}+{\dot I}_{\mathrm {L}} \\[ 5pt ] &=&419.89-\mathrm {j}314.92-\mathrm {j}188.00 \\[ 5pt ] &=&419.89-\mathrm {j}502.92 \ \mathrm {[A]} \\[ 5pt ] {\dot I}_{\mathrm {B}}^{\prime } &=&{\dot I}_{\mathrm {B}}-{\dot I}_{\mathrm {L}} \\[ 5pt ] &=&419.89-\mathrm {j}314.92+\mathrm {j}188.00 \\[ 5pt ] &=&419.89-\mathrm {j}126.92 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] となるので，その大きさ\( \ I_{\mathrm {A}}^{\prime } \ \mathrm {[A]} \ \)，\( \ I_{\mathrm {B}}^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {A}}^{\prime } &=&\sqrt {419.89^{2}+502.92^{2}} \\[ 5pt ] &≒&655.16　→　655 \ \mathrm {[A]} \\[ 5pt ] I_{\mathrm {B}}^{\prime } &=&\sqrt {419.89^{2}+126.92^{2}} \\[ 5pt ] &≒&438.65　→　439 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)b)両変圧器間のタップ段数の差によって生じる二つの変圧器で消費される遅れ無効電力の和の変化\( \ \Delta Q_{\mathrm {L}} \ \mathrm {[Mvar]} \ \)
両変圧器共に中間タップであるときの二つの変圧器で消費される遅れ無効電力を\( \ Q_{\mathrm {L}} \ \mathrm {[Mvar]} \ \)，変圧器\( \ \mathrm {A} \ \)のタップ段数を\( \ 3 \ \)段下げたときの二つの変圧器で消費される遅れ無効電力を\( \ Q_{\mathrm {L}}^{\prime } \ \mathrm {[Mvar]} \ \)とすると，
\[
\begin{eqnarray}
Q_{\mathrm {L}} &=&3\times 8.0\times I_{\mathrm {A}}^{2}+3\times 8.0\times I_{\mathrm {B}}^{2} \\[ 5pt ] &=&3\times 8.0\times 524.86^{2}+3\times 8.0\times 524.86^{2} \\[ 5pt ] &≒&13 \ 223 \ 000 \ \mathrm {[var]}　→　13.223 \ \mathrm {[Mvar]} \\[ 5pt ] Q_{\mathrm {L}}^{\prime } &=&3\times 8.0\times {I_{\mathrm {A}}^{\prime }}^{2}+3\times 8.0\times {I_{\mathrm {B}}^{\prime }}^{2} \\[ 5pt ] &=&3\times 8.0\times 655.16^{2}+3\times 8.0\times 438.65^{2} \\[ 5pt ] &≒&14 \ 920 \ 000 \ \mathrm {[var]}　→　14.920 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] となるので，消費される遅れ無効電力の変化\( \ \Delta Q_{\mathrm {L}} \ \mathrm {[Mvar]} \ \)は，
\[
\begin{eqnarray}
\Delta Q_{\mathrm {L}} &=&Q_{\mathrm {L}}^{\prime }-Q_{\mathrm {L}} \\[ 5pt ] &=&14.920-13.223 \\[ 5pt ] &=&1.697　→　1.70 \ \mathrm {[Mvar]} \\[ 5pt ] \end{eqnarray}
\] と求められる。