《電力・管理》〈配電〉[R03:問6]高調波発生負荷による高調波電流の大きさの導出に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

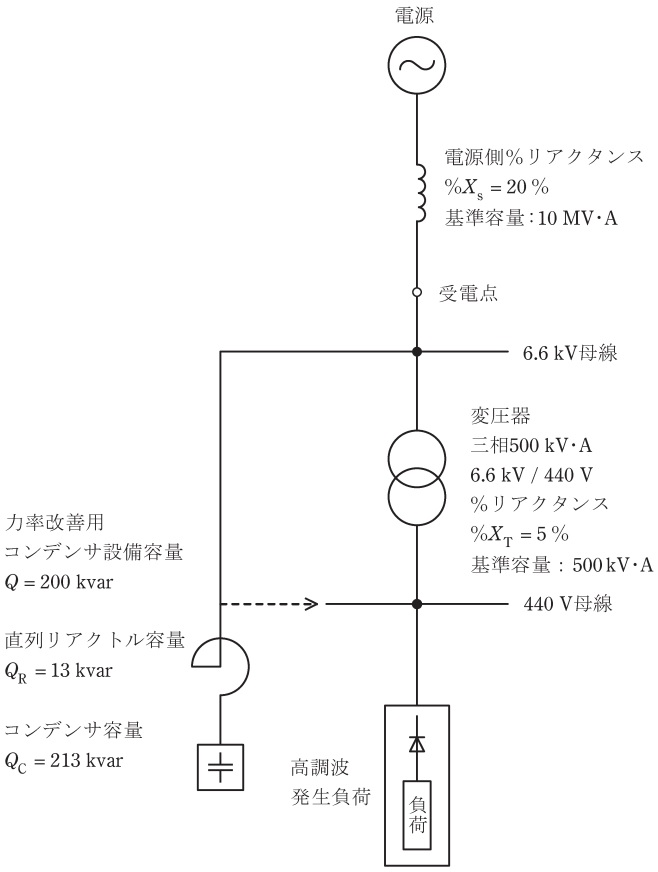
図は\( \ 6.6 \ \mathrm {kV} \ \)受電設備の単線結線図の一部である。変圧器の二次側\( \ 440 \ \mathrm {V} \ \)母線には高調波を発生する負荷が接続され，\( \ 6.6 \ \mathrm {kV} \ \)母線には力率改善用コンデンサ設備が設置されている。このとき次の問に答えよ。なお，力率改善用コンデンサ設備容量は，コンデンサと直列リアクトルを組み合わせた設備の定格電圧及び定格周波数（基本波）における無効電力とする。また，回路のインピーダンスは抵抗分を無視してリアクタンス分のみで計算せよ。

(1)　この負荷から発生する第\( \ 5 \ \)高調波電流の大きさを\( \ 440 \ \mathrm {V} \ \)基準で\( \ 20 \ \mathrm {A} \ \)とすると，\( \ 6.6 \ \mathrm {kV} \ \)の電源側に流出する第\( \ 5 \ \)高調波電流は何\( \ \mathrm {A} \ \)か。

(2)　力率改善用コンデンサ設備を\( \ 6.6 \ \mathrm {kV} \ \)母線から切り離し，定格電圧を\( \ 440 \ \mathrm {V} \ \)に変更した上で，図の点線で示すように\( \ 440 \ \mathrm {V} \ \)母線に設置した場合，\( \ 6.6 \ \mathrm {kV} \ \)電源側に流出する第\( \ 5 \ \)高調波電流は何\( \ \mathrm {A} \ \)か。
　ただし，力率改善用コンデンサ設備のコンデンサ容量及び直列リアクトル容量は変えないものとする。

【ワンポイント解説】

負荷から電源側に流れる高調波電流の計算に関する問題です。
\( \ 2 \ \)種でも平成25年問5に類題が出題されており，\( \ 1 \ \)種受験生であるとほとんどの受験生が一度は取り組んだことがある内容であると思うので，確実に理解するようにして下さい。

1.オーム法から単位法への変換
基準容量\( \ P_{\mathrm {n}} \ \mathrm {[V\cdot A]} \ \)，基準電圧\( \ V_{\mathrm {n}} \ \mathrm {[V]} \ \)，基準電流\( \ I_{\mathrm {n}} \ \mathrm {[A]} \ \)の時，インピーダンス\( \ Z \ \mathrm {[\Omega ]} \ \)を単位法で表すと，
\[
\begin{eqnarray}
Z \ \mathrm {[p.u.]} \ &=&\frac {Z \ [\Omega ] \ I_{\mathrm {n}}}{\displaystyle \frac {V_{\mathrm {n}}}{\sqrt {3}}} (定義) \\[ 5pt ] &=&\frac {\sqrt {3}Z \ [\Omega ] \ I_{\mathrm {n}}}{V_{\mathrm {n}}} \\[ 5pt ] &=&\frac {\sqrt {3}Z \ [\Omega ] \ V_{\mathrm {n}}I_{\mathrm {n}}}{V_{\mathrm {n}}^{2}} \\[ 5pt ] &=&\frac {P_{\mathrm {n}}Z \ [\Omega ] \ }{V_{\mathrm {n}}^{2}}　　 (∵P_{\mathrm {n}}=\sqrt {3}V_{\mathrm {n}}I_{\mathrm {n}} ) \\[ 5pt ] \end{eqnarray}
\] となります。

2.単位法における容量換算
「1.オーム法から単位法への変換」の通り，単位法のインピーダンスは基準容量に比例します。したがって，基準容量\( \ P_{\mathrm {A}} \ \)から\( \ P_{\mathrm {B}} \ \)へ変換する場合の単位法におけるインピーダンスは，
\[
\begin{eqnarray}
Z_{\mathrm {B}} \ \mathrm {[p.u.]}&=&\frac {P_{\mathrm {B}}}{P_{\mathrm {A}}}Z_{\mathrm {A}} \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となります。

3.コイル，コンデンサのリアクタンス
コイル\( \ L \ \mathrm {[H]} \ \)，コンデンサ\( \ C \ \mathrm {[F]} \ \)があり，電源周波数\( \ f \ \mathrm {[Hz]} \ \)が与えられているとき，それぞれのリアクタンス\( \ X_{\mathrm {L}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C}} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L}}&=&\mathrm {j}\omega L \\[ 5pt ] &=&\mathrm {j}2\pi f L \\[ 5pt ] -\mathrm {j}X_{\mathrm {C}}&=&\frac {1}{\mathrm {j}\omega C} \\[ 5pt ] &=&\frac {1}{\mathrm {j}2\pi f C}\left( \frac {1}{\mathrm {j}}=\frac {1}{\mathrm {j}}\times \frac {\mathrm {j}}{\mathrm {j}}=-\mathrm {j}\right) \\[ 5pt ] \end{eqnarray}
\] で求められます。したがって，第\( \ 5 \ \)次高調波に対するリアクタンス\( \ X_{\mathrm {L5}} \ \mathrm {[\Omega ]} \ \)及び\( \ X_{\mathrm {C5}} \ \mathrm {[\Omega ]} \ \)は，周波数が\( \ 5 \ \)倍となるので，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {L5}}&=&\mathrm {j}2\pi \times 5f \times L \\[ 5pt ] &=&\mathrm {j}5 X_{\mathrm {L}} \\[ 5pt ] -\mathrm {j}X_{\mathrm {C5}}&=&\frac {1}{\mathrm {j}2\pi \times 5f \times C} \\[ 5pt ] &=&-\mathrm {j}\frac {X_{\mathrm {C5}}}{5} \\[ 5pt ] \end{eqnarray}
\] となります。

【解答】

(1)負荷から発生する第\( \ 5 \ \)高調波電流の大きさを\( \ 440 \ \mathrm {V} \ \)基準で\( \ 20 \ \mathrm {A} \ \)とすると，\( \ 6.6 \ \mathrm {kV} \ \)の電源側に流出する第\( \ 5 \ \)高調波電流は何\( \ \mathrm {A} \ \)か
基準容量を\( \ P_{\mathrm {n}}=10 \ \mathrm {[MV\cdot A]} \ \)とする。
ワンポイント解説「1.オーム法から単位法への変換」及びワンポイント解説「2.単位法における容量換算」の通り，各リアクタンスを単位法に変換すると，電源側リアクタンス\( \ \mathrm {j}X_{\mathrm {S}} \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {S}} \ \mathrm {[p.u.]}&=& \mathrm {j}0.2 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] 変圧器のリアクタンス\( \ \mathrm {j}X_{\mathrm {T}} \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {T}} \ \mathrm {[p.u.]}&=&\frac {10\times 10^{6}}{500\times 10^{3}}\times \mathrm {j}0.05 \\[ 5pt ] &=& \mathrm {j}1.0 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。力率改善用コンデンサ設備容量は，コンデンサと直列リアクトルを組み合わせた設備の定格電圧及び定格周波数（基本波）における無効電力であるから，そのリアクタンスは自己容量基準で\( \ 1.0 \ \mathrm {p.u.} \ \)であるので，
\[
\begin{eqnarray}
\mathrm {j}X \ \mathrm {[p.u.]}&=&\frac {10\times 10^{6}}{200\times 10^{3}}\times \mathrm {j}1.0 \\[ 5pt ] &=& \mathrm {j}50.0 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となり，直列リアクトルのリアクタンス\( \ \mathrm {j}X_{\mathrm {R}} \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
\mathrm {j}X_{\mathrm {R}} \ \mathrm {[p.u.]}&=&\frac {13}{200}\times \mathrm {j}50.0 \ \mathrm {[p.u.]} \\[ 5pt ] &=& \mathrm {j}3.25 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] コンデンサのリアクタンス\( \ -\mathrm {j}X_{\mathrm {C}} \ \mathrm {[p.u.]} \ \)は，
\[
\begin{eqnarray}
-\mathrm {j}X_{\mathrm {C}} \ \mathrm {[p.u.]}&=&\frac {-213}{200}\times \mathrm {j}50.0 \ \mathrm {[p.u.]} \\[ 5pt ] &=& -\mathrm {j}53.25 \ \mathrm {[p.u.]} \\[ 5pt ] \end{eqnarray}
\] となる。変圧器二次側での第\( \ 5 \ \)高調波電流の大きさが\( \ I_{2}=20 \ \mathrm {[A]} \ \)であるから，一次側換算すると，
\[
\begin{eqnarray}
I_{1}&=&\frac {V_{2}}{V_{1}}\times I_{2} \\[ 5pt ] &=&\frac {440}{6.6\times 10^{3}}\times 20 \\[ 5pt ] &≒& 1.3333 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] であるため，ワンポイント解説「3.コイル，コンデンサのリアクタンス」の通り，第\( \ 5 \ \)高調波に分流の法則を適用すれば，電源側に流出する電流の大きさ\( \ I_{\mathrm {5s}} \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {5s}}&=&\frac {\mathrm {j}5X_{\mathrm {R}}-\displaystyle \mathrm {j}\frac {X_{\mathrm {C}}}{5}}{\mathrm {j}5X_{\mathrm {S}}+\mathrm {j}5X_{\mathrm {R}}-\displaystyle \mathrm {j}\frac {X_{\mathrm {C}}}{5}}\times I_{1} \\[ 5pt ] &=&\frac {\mathrm {j}5\times 3.25-\displaystyle \mathrm {j}\frac {53.25}{5}}{\mathrm {j}5\times 0.2+\mathrm {j}5\times 3.25-\displaystyle \mathrm {j}\frac {53.25}{5}}\times 1.3333 \\[ 5pt ] &=&\frac {5.6}{6.6}\times 1.3333 \\[ 5pt ] &≒& 1.1313　→　1.13 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)図の点線で示すように\( \ 440 \ \mathrm {V} \ \)母線に設置した場合，\( \ 6.6 \ \mathrm {kV} \ \)電源側に流出する第\( \ 5 \ \)高調波電流は何\( \ \mathrm {A} \ \)か
(1)と同様に，第\( \ 5 \ \)高調波に分流の法則を適用すれば，電源側に流出する電流の大きさ\( \ I_{\mathrm {5s}}^{\prime } \ \mathrm {[A]} \ \)は，
\[
\begin{eqnarray}
I_{\mathrm {5s}}^{\prime }&=&\frac {\mathrm {j}5X_{\mathrm {R}}-\displaystyle \mathrm {j}\frac {X_{\mathrm {C}}}{5}}{\mathrm {j}5X_{\mathrm {S}}+\mathrm {j}5X_{\mathrm {T}}+\mathrm {j}5X_{\mathrm {R}}-\displaystyle \mathrm {j}\frac {X_{\mathrm {C}}}{5}}\times I_{1} \\[ 5pt ] &=&\frac {\mathrm {j}5\times 3.25-\displaystyle \mathrm {j}\frac {53.25}{5}}{\mathrm {j}5\times 0.2+\mathrm {j}5\times 1.0+\mathrm {j}5\times 3.25-\displaystyle \mathrm {j}\frac {53.25}{5}}\times 1.3333 \\[ 5pt ] &=&\frac {5.6}{11.6}\times 1.3333 \\[ 5pt ] &≒& 0.64366　→　0.644 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。