【問題】
【難易度】★★★☆☆(普通)
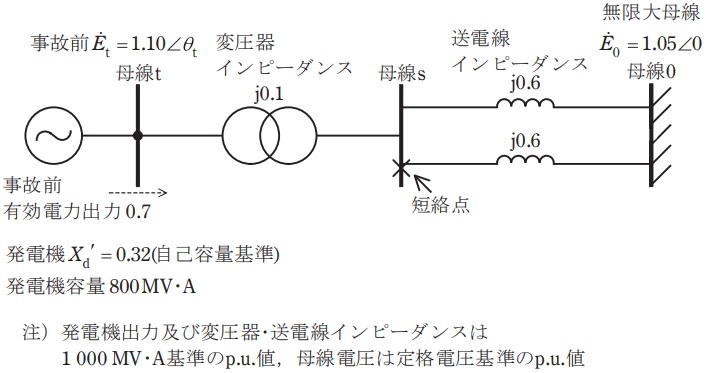
図の系統で,\( \ 2 \ \)回線送電線の母線\( \ \mathrm {s} \ \)で\( \ \mathrm {bc} \ \)相\( \ 2 \ \)相短絡故障が発生したときの正相短絡電流及びそのときの母線\( \ \mathrm {s} \ \)の正相電圧を,対称座標法を用いて次の手順で求めよ。なお,計算には単位法を用い,系統及び発電機の逆相インピーダンスは全て正相インピーダンスと同じとする。また,短絡前の各母線の電圧位相\( \ \theta \ \mathrm {[rad]} \ \)は\( \ \displaystyle \left| \theta \right| <\frac {\pi }{2} \ \)とする。
(1) 短絡前の母線\( \ \mathrm {s} \ \)の電圧を\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[p.u.]} \ \),同母線から系統を見た正相インピーダンスを\( \ {\dot Z}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)とするとき,母線\( \ \mathrm {s} \ \)における\( \ \mathrm {bc} \ \)相\( \ 2 \ \)相短絡故障時の正相短絡電流\( \ {\dot I}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)の式を求めよ。
(2) 図の値を用いて\( \ \sin \theta _{\mathrm {t}} \ \)の値を求め,これを用いて短絡前の母線\( \ \mathrm {s} \ \)の電圧の絶対値\( \ E_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)を求めよ。
(3) 図の値を用いて,母線\( \ \mathrm {s} \ \)から系統を見た正相インピーダンス\( \ {\dot Z}_{\mathrm {s1}} \ \)の値\( \ \mathrm {[p.u.]} \ \)を求めよ。
(4) 上記\( \ \mathrm {bc} \ \)相\( \ 2 \ \)相短絡故障時の正相短絡電流の絶対値\( \ I_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \),及びこのときの母線\( \ \mathrm {s} \ \)の正相電圧の絶対値\( \ V_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)を求めよ。
【ワンポイント解説】
対称座標法を用い正相短絡電流と正相電圧を求める問題です。
(1)が最も知識を必要とする内容なので,(1)がクリアできると完答も目指せる問題かと思います。
対称座標法は数学的な定義のような内容で,\( \ 1 \ \)種では必須の知識となりますので,必ず覚えるようにしましょう。
1.ベクトルオペレータ\( \ a \ \)
ベクトルオペレータ\( \ a \ \)は,\( \ a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}} \ \)で定義される演算子であり,
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} \\[ 5pt ]
&=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ]
a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} \\[ 5pt ]
&=& 1 \\[ 5pt ]
\end{eqnarray}
\]
となります。上記より,
\[
\begin{eqnarray}
\overline {a} &=& a^{2} \\[ 5pt ]
1+a+a^{2}&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
の関係があることがわかります。
2.対称座標法
故障計算をする際に非常に便利な方法で,以下のように定義し対称座標変換されます。
零相電圧\( \ {\dot V}_{0} \ \),正相電圧\( \ {\dot V}_{1} \ \),逆相電圧\( \ {\dot V}_{2} \ \)とすると,各相の電圧\( \ {\dot V}_{\mathrm {a}} \ \),\( \ {\dot V}_{\mathrm {b}} \ \),\( \ {\dot V}_{\mathrm {c}} \ \)は以下のように表せます。
\[
\begin{eqnarray}
{\dot V}_{\mathrm {a}} &=&{\dot V}_{0}+ {\dot V}_{1} + {\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {b}} &=&{\dot V}_{0}+ a^{2}{\dot V}_{1} + a{\dot V}_{2} \\[ 5pt ]
{\dot V}_{\mathrm {c}} &=&{\dot V}_{0}+ a{\dot V}_{1} + a^{2}{\dot V}_{2} \\[ 5pt ]
\end{eqnarray}
\]
零相電流\( \ {\dot I}_{0} \ \),正相電流\( \ {\dot I}_{1} \ \),逆相電流\( \ {\dot I}_{2} \ \)とすると,各相の電流\( \ {\dot I}_{\mathrm {a}} \ \),\( \ {\dot I}_{\mathrm {b}} \ \),\( \ {\dot I}_{\mathrm {c}} \ \)は電圧同様に以下のように表せます。
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=&{\dot I}_{0}+ {\dot I}_{1} + {\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {b}} &=&{\dot I}_{0}+ a^{2}{\dot I}_{1} + a{\dot I}_{2} \\[ 5pt ]
{\dot I}_{\mathrm {c}} &=&{\dot I}_{0}+ a{\dot I}_{1} + a^{2}{\dot I}_{2} \\[ 5pt ]
\end{eqnarray}
\]
また,対称座標法における発電機の基本式は以下の通りとなります。
\[
\begin{eqnarray}
{\dot V}_{0} &=&-{\dot Z}_{0}{\dot I}_{0} \\[ 5pt ]
{\dot V}_{1} &=&{\dot E}_{\mathrm {a}}-{\dot Z}_{1}{\dot I}_{1} \\[ 5pt ]
{\dot V}_{2} &=&-{\dot Z}_{2}{\dot I}_{2}
\end{eqnarray}
\]
3.送電線の送電電力
送電端の電圧が\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \),受電端の電圧が\( \ V_{\mathrm {r}} \ \mathrm {[V]} \ \),送電線の\( \ 1 \ \)線あたりのリアクタンスが\( \ x \ \mathrm {[\Omega ]} \ \)(抵抗分は無視できるものとします),送電線に流れる電流が\( \ I \ \mathrm {[A]} \ \)であるとすると,送電線の単線結線図は図1,ベクトル図は図2のように描くことができます。ただし,\( \ \delta \ \mathrm {[rad]} \ \)は送電端電圧と受電端電圧の相差角,\( \ \theta \ \mathrm {[rad]} \ \)は負荷の力率角,\( \ E_{\mathrm {s}} \ \mathrm {[V]} \ \)は送電端の相電圧,\( \ E_{\mathrm {r}} \ \mathrm {[V]} \ \)は受電端の相電圧です。
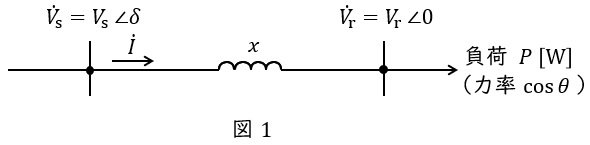
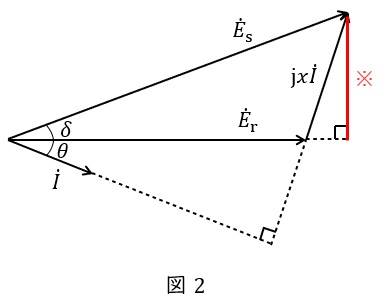
このとき,負荷電力\( \ P \ \mathrm {[W]} \ \)は,
\[
\begin{eqnarray}
P&=&\sqrt {3} V_{\mathrm {r}}I\cos \theta \\[ 5pt ]
\end{eqnarray}
\]
で求めることができ,図2の※線を求める式より,
\[
\begin{eqnarray}
xI\cos \theta &=&E_{\mathrm {s}}\sin \delta \\[ 5pt ]
I\cos \theta &=&\frac {E_{\mathrm {s}}}{x}\sin \delta \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}}{\sqrt {3}x}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
P&=&\sqrt {3} V_{\mathrm {r}}I\cos \theta \\[ 5pt ]
&=&\sqrt {3} V_{\mathrm {r}}\cdot \frac {V_{\mathrm {s}}}{\sqrt {3}x}\sin \delta \\[ 5pt ]
&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{x}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
となります。上式は\( \ P=\sqrt {3} V_{\mathrm {r}}I\cos \theta \ \)と合わせて公式として覚えておきましょう。
【解答】
(1)母線\( \ \mathrm {s} \ \)における\( \ \mathrm {bc} \ \)相\( \ 2 \ \)相短絡故障時の正相短絡電流\( \ {\dot I}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)の式
母線\( \ \mathrm {s} \ \)における各相の電圧を\( \ {\dot V}_{\mathrm {sa}} \ \mathrm {[p.u.]} \ \),\( \ {\dot V}_{\mathrm {sb}} \ \mathrm {[p.u.]} \ \),\( \ {\dot V}_{\mathrm {sc}} \ \mathrm {[p.u.]} \ \),各相の電流を\( \ {\dot I}_{\mathrm {sa}} \ \mathrm {[p.u.]} \ \),\( \ {\dot I}_{\mathrm {sb}} \ \mathrm {[p.u.]} \ \),\( \ {\dot I}_{\mathrm {sc}} \ \mathrm {[p.u.]} \ \)とする。母線\( \ \mathrm {s} \ \)における零相電圧,正相電圧,逆相電圧を\( \ {\dot V}_{\mathrm {s0}} \ \mathrm {[p.u.]} \ \),\( \ {\dot V}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \),\( \ {\dot V}_{\mathrm {s2}} \ \mathrm {[p.u.]} \ \),零相電流,正相電流,逆相電流を\( \ {\dot I}_{\mathrm {s0}} \ \mathrm {[p.u.]} \ \),\( \ {\dot I}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \),\( \ {\dot I}_{\mathrm {s2}} \ \mathrm {[p.u.]} \ \)とする。
ワンポイント解説「2.対称座標法」に沿って,各電圧電流の関係式を立てると,\( \ \mathrm {bc} \ \)相\( \ 2 \ \)相短絡故障時は,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {sa}} &=&{\dot V}_{\mathrm {s0}}+ {\dot V}_{\mathrm {s1}} + {\dot V}_{\mathrm {s2}} &・・・・・・・・・・ ①& \\[ 5pt ]
{\dot V}_{\mathrm {sb}} &=&{\dot V}_{\mathrm {s0}}+ a^{2}{\dot V}_{\mathrm {s1}} + a{\dot V}_{\mathrm {s2}}={\dot V}_{\mathrm {sc}} &・・・・・・・・・・ ②& \\[ 5pt ]
{\dot V}_{\mathrm {sc}} &=&{\dot V}_{\mathrm {s0}}+ a{\dot V}_{\mathrm {s1}} + a^{2}{\dot V}_{\mathrm {s2}}={\dot V}_{\mathrm {sb}} &・・・・・・・・・・ ③& \\[ 5pt ]
{\dot I}_{\mathrm {sa}} &=&{\dot I}_{\mathrm {s0}}+ {\dot I}_{\mathrm {s1}} + {\dot I}_{\mathrm {s2}}=0 &・・・・・・・・・・ ④& \\[ 5pt ]
{\dot I}_{\mathrm {sb}} &=&{\dot I}_{\mathrm {s0}}+ a^{2}{\dot I}_{\mathrm {s1}} + a{\dot I}_{\mathrm {s2}}=-{\dot I}_{\mathrm {sc}} &・・・・・・・・・・ ⑤& \\[ 5pt ]
{\dot I}_{\mathrm {sc}} &=&{\dot I}_{\mathrm {s0}}+ a{\dot I}_{\mathrm {s1}} + a^{2}{\dot I}_{\mathrm {s2}}=-{\dot I}_{\mathrm {sb}} &・・・・・・・・・・ ⑥& \\[ 5pt ]
\end{eqnarray}
\]
である。\( \ ② \ \)及び\( \ ③ \ \)より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s0}}+ a^{2}{\dot V}_{\mathrm {s1}} + a{\dot V}_{\mathrm {s2}} &=&{\dot V}_{\mathrm {s0}}+ a{\dot V}_{\mathrm {s1}} + a^{2}{\dot V}_{\mathrm {s2}} \\[ 5pt ]
a^{2}{\dot V}_{\mathrm {s1}} + a{\dot V}_{\mathrm {s2}} &=&a{\dot V}_{\mathrm {s1}} + a^{2}{\dot V}_{\mathrm {s2}} \\[ 5pt ]
a^{2}{\dot V}_{\mathrm {s1}} -a{\dot V}_{\mathrm {s1}} &=&a^{2}{\dot V}_{\mathrm {s2}}-a{\dot V}_{\mathrm {s2}} \\[ 5pt ]
\left( a^{2}-a\right) {\dot V}_{\mathrm {s1}} &=&\left( a^{2}-a\right) {\dot V}_{\mathrm {s2}} \\[ 5pt ]
{\dot V}_{\mathrm {s1}} &=&{\dot V}_{\mathrm {s2}} ・・・・・・・・・・ ⑦ \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ④+⑤+⑥ \ \)より,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {sa}}+{\dot I}_{\mathrm {sb}} + {\dot I}_{\mathrm {sc}}&=&3{\dot I}_{\mathrm {s0}} \left( ∵1+a+a^{2}=0\right) \\[ 5pt ]
0+{\dot I}_{\mathrm {sb}} – {\dot I}_{\mathrm {sb}}&=&3{\dot I}_{\mathrm {s0}} \\[ 5pt ]
{\dot I}_{\mathrm {s0}} &=&0 \ ・・・・・・・・・・ ⑧ \\[ 5pt ]
\end{eqnarray}
\]
であるから,これと\( \ ⑤ \ \)及び\( \ ⑥ \ \)より,
\[
\begin{eqnarray}
a^{2}{\dot I}_{\mathrm {s1}} + a{\dot I}_{\mathrm {s2}} &=&-\left( a{\dot I}_{\mathrm {s1}} + a^{2}{\dot I}_{\mathrm {s2}}\right) \\[ 5pt ]
a^{2}{\dot I}_{\mathrm {s1}} + a{\dot I}_{\mathrm {s1}} &=&- a^{2}{\dot I}_{\mathrm {s2}}-a{\dot I}_{\mathrm {s2}} \\[ 5pt ]
\left( a^{2}+a\right) {\dot I}_{\mathrm {s1}} &=&-\left( a^{2}+a\right) {\dot I}_{\mathrm {s2}} \\[ 5pt ]
{\dot I}_{\mathrm {s1}} &=&- {\dot I}_{\mathrm {s2}} \ \ ・・・・・・・・・・ ⑨ \\[ 5pt ]
\end{eqnarray}
\]
となる。また,発電機の基本式は,零相インピーダンス,正相インピーダンス,逆相インピーダンスをそれぞれ\( \ {\dot Z}_{\mathrm {s0}} \ \mathrm {[p.u.]} \ \),\( \ {\dot Z}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \),\( \ {\dot Z}_{\mathrm {s2}}={\dot Z}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)(問題文より)とすると,ワンポイント解説「2.対称座標法」の通り,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s0}} &=&-{\dot Z}_{\mathrm {s0}}{\dot I}_{\mathrm {s0}} \ &・・・・・・・・・・ ⑩& \\[ 5pt ]
{\dot V}_{\mathrm {s1}} &=&{\dot E}_{\mathrm {s}}-{\dot Z}_{\mathrm {s1}}{\dot I}_{\mathrm {s1}} &・・・・・・・・・・ ⑪& \\[ 5pt ]
{\dot V}_{\mathrm {s2}} &=&-{\dot Z}_{\mathrm {s1}}{\dot I}_{\mathrm {s2}} &・・・・・・・・・・ ⑫& \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ ⑧ \ \)及び\( \ ⑩ \ \)より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s0}} &=&-{\dot Z}_{\mathrm {s0}}{\dot I}_{\mathrm {s0}} \\[ 5pt ]
&=&-{\dot Z}_{\mathrm {s0}}\times 0 \\[ 5pt ]
&=& 0 \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ ⑦ \ \),\( \ ⑪ \ \)及び\( \ ⑫ \ \)より,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}}-{\dot Z}_{\mathrm {s1}}{\dot I}_{\mathrm {s1}} &=&-{\dot Z}_{\mathrm {s1}}{\dot I}_{\mathrm {s2}} \\[ 5pt ]
{\dot E}_{\mathrm {s}}-{\dot Z}_{\mathrm {s1}}{\dot I}_{\mathrm {s1}} &=&{\dot Z}_{\mathrm {s1}}{\dot I}_{\mathrm {s1}} \left( ∵⑨\right) \\[ 5pt ]
{\dot E}_{\mathrm {s}} &=&2{\dot Z}_{\mathrm {s1}}{\dot I}_{\mathrm {s1}} \\[ 5pt ]
{\dot I}_{\mathrm {s1}}&=&\frac {{\dot E}_{\mathrm {s}}}{2{\dot Z}_{\mathrm {s1}}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ \sin \theta _{\mathrm {t}} \ \)の値と短絡前の母線\( \ \mathrm {s} \ \)の電圧の絶対値\( \ E_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)
母線\( \ \mathrm {t} \ \)から,無限大母線までのリアクタンス\( \ X \ \mathrm {[p.u.]} \ \)は,変圧器のリアクタンス\( \ X_{\mathrm {T}}=0.1 \ \mathrm {[p.u.]} \ \)及び送電線インピーダンス\( \ X_{\mathrm {l}}=0.6 \ \mathrm {[p.u.]} \ \)より,
\[
\begin{eqnarray}
X &=&X_{\mathrm {T}}+\frac {X_{\mathrm {l}}}{2} \\[ 5pt ]
&=&0.1+\frac {0.6}{2} \\[ 5pt ]
&=&0.4 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,事故前有効電力出力\( \ P=0.7 \ \mathrm {[p.u.]} \ \)を求める式より\( \ \sin \theta _{\mathrm {t}} \ \)は,ワンポイント解説「3.送電線の送電電力」の通り,
\[
\begin{eqnarray}
P &=&\frac {E_{\mathrm {t}}E_{\mathrm {0}}}{X}\sin \theta _{\mathrm {t}} \\[ 5pt ]
\sin \theta _{\mathrm {t}} &=&\frac {XP}{E_{\mathrm {t}}E_{\mathrm {0}}} \\[ 5pt ]
&=&\frac {0.4\times 0.7}{1.10\times 1.05} \\[ 5pt ]
&≒&0.242 \ 42 → 0.242 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。これより,\( \ \cos \theta _{\mathrm {t}} \ \)は,
\[
\begin{eqnarray}
\cos \theta _{\mathrm {t}} &=&\sqrt {1-\sin ^{2}\theta _{\mathrm {t}}} \\[ 5pt ]
&=&\sqrt {1-0.242 \ 42 ^{2}} \\[ 5pt ]
&≒&0.970 \ 17 \ \mathrm {[rad]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,短絡前の母線\( \ \mathrm {t} \ \)の電圧\( \ {\dot E}_{\mathrm {t}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {t}} &=&E_{\mathrm {t}}\left( \cos \theta _{\mathrm {t}}+\mathrm {j}\sin \theta _{\mathrm {t}} \right) \\[ 5pt ]
&=&1.10\times \left( 0.970 \ 17+\mathrm {j}0.242 \ 42 \right) \\[ 5pt ]
&≒&1.067 \ 2+\mathrm {j}0.266 \ 66 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,短絡前の母線\( \ \mathrm {s} \ \)の電圧\( \ {\dot E}_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)は,分圧の法則より,
\[
\begin{eqnarray}
{\dot E}_{\mathrm {s}} &=&{\dot E}_{\mathrm {0}}+\frac {\displaystyle \frac {X_{\mathrm {l}}}{2}}{\displaystyle X_{\mathrm {T}}+\frac {X_{\mathrm {l}}}{2}}\left( {\dot E}_{\mathrm {t}}-{\dot E}_{\mathrm {0}}\right) \\[ 5pt ]
&=&\left( 1.05+\mathrm {j}0 \right) +\frac {\displaystyle \frac {0.6}{2}}{\displaystyle 0.1+\frac {0.6}{2}}\times \left\{ \left( 1.067 \ 2+\mathrm {j}0.266 \ 66 \right) -\left( 1.05+\mathrm {j}0 \right) \right\} \\[ 5pt ]
&=&1.05+0.75\times \left( 0.017 \ 2+\mathrm {j}0.266 \ 66 \right) \\[ 5pt ]
&≒&1.062 \ 9+\mathrm {j}0.200 \ 00 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
となるから,その絶対値\( \ E_{\mathrm {s}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
E_{\mathrm {s}} &=&\sqrt {1.062 \ 9^{2}+0.200 \ 00^{2}} \\[ 5pt ]
&≒&1.081 \ 6 → 1.08 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)母線\( \ \mathrm {s} \ \)から系統を見た正相インピーダンス\( \ {\dot Z}_{\mathrm {s1}} \ \)の値\( \ \mathrm {[p.u.]} \ \)
発電機のリアクタンスを\( \ 1 \ 000 \ \mathrm {[MV\cdot A]} \ \)換算したリアクタンス\( \ {X_{\mathrm {d}}}^{\prime \prime } \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{X_{\mathrm {d}}}^{\prime \prime } &=&\frac {1 \ 000}{800}\times {X_{\mathrm {d}}}^{\prime } \\[ 5pt ]
&=&\frac {1 \ 000}{800}\times 0.32 \\[ 5pt ]
&=&0.40 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であり,事故発生時,短絡点から発電機側を見たインピーダンス及び系統側を見たインピーダンスは並列であるから,母線\( \ \mathrm {s} \ \)から見た正相インピーダンス\( \ {\dot Z}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot Z}_{\mathrm {s1}} &=&\frac {\displaystyle \left( \mathrm {j}{X_{\mathrm {d}}}^{\prime \prime }+\mathrm {j}X_{\mathrm {T}}\right) \frac {\mathrm {j}X_{\mathrm {l}}}{2}}{\displaystyle \left( \mathrm {j}{X_{\mathrm {d}}}^{\prime \prime }+\mathrm {j}X_{\mathrm {T}}\right) +\frac {\mathrm {j}X_{\mathrm {l}}}{2}} \\[ 5pt ]
&=&\frac {\displaystyle \left( \mathrm {j}0.40+\mathrm {j}0.10\right) \times \frac {\mathrm {j}0.6}{2}}{\displaystyle \left( \mathrm {j}0.40+\mathrm {j}0.10\right) + \frac {\mathrm {j}0.6}{2}} \\[ 5pt ]
&=&\mathrm {j}0.187 \ 5 → 0.188 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)\( \ \mathrm {bc} \ \)相\( \ 2 \ \)相短絡故障時の正相短絡電流の絶対値\( \ I_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)及び母線\( \ \mathrm {s} \ \)の正相電圧の絶対値\( \ V_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)
(1)~(3)より,正相短絡電流\( \ {\dot I}_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
{\dot I}_{\mathrm {s1}}&=&\frac {{\dot E}_{\mathrm {s}}}{2{\dot Z}_{\mathrm {s1}}} \\[ 5pt ]
&=&\frac {1.062 \ 9+\mathrm {j}0.200 \ 00}{2\times \mathrm {j}0.1875} \\[ 5pt ]
&≒&0.533 \ 33-\mathrm {j}2.8344 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
であるから,その絶対値\( \ I_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
I_{\mathrm {s1}}&=&\sqrt {0.533 \ 33^{2}+2.834 \ 4^{2}} \\[ 5pt ]
&≒&2.884 \ 1 → 2.88 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ ⑪ \ \)より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {s1}} &=&{\dot E}_{\mathrm {s}}-{\dot Z}_{\mathrm {s1}}{\dot I}_{\mathrm {s1}} \\[ 5pt ]
&=&{\dot E}_{\mathrm {s}}-{\dot Z}_{\mathrm {s1}}\frac {{\dot E}_{\mathrm {s}}}{2{\dot Z}_{\mathrm {s1}}} \\[ 5pt ]
&=&\frac {{\dot E}_{\mathrm {s}}}{2} \\[ 5pt ]
&=&\frac {1.062 \ 9+\mathrm {j}0.200 \ 00 }{2} \\[ 5pt ]
&=&0.531 \ 45+\mathrm {j}0.100 \ 00 \\[ 5pt ]
\end{eqnarray}
\]
となるので,その絶対値\( \ V_{\mathrm {s1}} \ \mathrm {[p.u.]} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {s1}} &=&\sqrt {0.531 \ 45^{2}+0.100 \ 00^{2}} \\[ 5pt ]
&≒&0.540 \ 78 → 0.541 \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん