【問題】
【難易度】★★★☆☆(普通)
次の文章は,電力系統の安定度に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
電力系統に並列運転する同期発電機は,系統から受けるじょう乱に対して同期運転を維持するための安定条件が必要であり,これを電力系統の安定度と呼んでいる。安定度は,対象とする時間領域や,じょう乱の大きさにより下表の分類で区分されることが多い。
\[
\begin{array}{|c|l|}
\hline
\ \fbox { (1) } \ 安定度 & 電力系統が並行運転状態にあって,ごく微小なじょう乱 \\
& が加わったときに動揺が収まり元の状態に戻るか否かの \\
& 安定度。 \\
\hline
\ \fbox { (2) } \ 安定度 & 電力系統に加わるじょう乱が比較的大きい場合で,じょ \\
& う乱からの経過時間がごく短い領域の現象を対象とした \\
& 安定度。 \\
\hline
\ \fbox { (3) } \ 安定度 & \ \fbox { (2) } \ 安定度の領域に引き続く領域の現象を対象と \\
& し,励磁系や調速系などが重要な役割を持つ。 \\
\hline
\ \fbox { (4) } \ 動特性 & \ \fbox { (3) } \ 安定度領域よりも電圧安定性や周波数変動と \\
& いった \ \fbox { (4) } \ の領域の動特性を対象とする。 \\
\hline
\end{array}
\]
\( \ \fbox { (1) } \ \)安定度の向上対策としては,系統に\( \ \fbox { (5) } \ \)を接続する方法があるが\( \ \fbox { (5) } \ \)で補償された送電系統の共振周波数と,発電機の\( \ \fbox { (6) } \ \)とで低周波共振現象が発生する可能性があることからほとんど採用されていない。実際には,送電電圧の昇圧や,諸外国で採用されている\( \ \fbox { (7) } \ \)などが効果的である。
\( \ \fbox { (2) } \ \)安定度や\( \ \fbox { (3) } \ \)安定度の向上対策としては,送電線事故時の遮断時間や再閉路時間を短縮して事故によるじょう乱の影響を少なくする方法や,発電機の\( \ \fbox { (8) } \ \)を大きくすることで不安定に至るまでの時間を延ばす方法なども効果がある。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& 持 続 &(ロ)& 短時間 &(ハ)& 磁気飽和共振周波数 \\[ 5pt ]
&(ニ)& 分路リアクトル &(ホ)& 直列コンデンサ &(ヘ)& 応 動 \\[ 5pt ]
&(ト)& 定 態 &(チ)& 同期リアクタンス &(リ)& 慣性定数 \\[ 5pt ]
&(ヌ)& \mathrm {HVDC} \ 送電 &(ル)& 過 渡 &(ヲ)& ガバナ・フリー運転 \\[ 5pt ]
&(ワ)& 動 態 &(カ)& 長時間 &(ヨ)& 並列コンデンサ \\[ 5pt ]
&(タ)& \mathrm {TBC} &(レ)& 励磁制御系の共振周波数 &(ソ)& 瞬 時 \\[ 5pt ]
&(ツ)& 過渡リアクタンス &(ネ)& 軸ねじり共振周波数 && \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
安定度に関する問題です。
電験\( \ 2 \ \)種までは,ほぼ定態安定度と過渡安定度の違いやそれぞれの概要を問うような問題が出題されていたと思いますが,本問では動態安定度や長時間動特性に関する内容が出題されています。
専門書においては,微分方程式を扱ったような定量的な内容が説明されていることもあると思いますが,電験では用語と概要を知っておけば十分かと思います。
1.安定度の種類
①定態安定度
日常的な負荷の増加や減少,送電線の停止操作等の変動に対し,安定運転できる度合いを言います。
②過渡安定度
事故等の大きな擾(じょう)乱が発生した際に,運転を継続できる度合いを言います。動態安定度と区別する場合は,制御装置を伴わない経過時間の短い領域(通常\( \ 1 \ \)秒程度以内)を対象とします。
③動態安定度
過渡安定度のうち,電圧調整装置やガバナ等の自動制御装置を考慮した運転を継続できる度合いを言います。過渡安定度から引き続く領域を対象とします。近年は高速応答制御が可能となっているので,過渡安定度と区別しないことも多いです。
④長時間動特性
\( \ 1 \ \)分以上の比較的長い電圧変化や周波数変動に対する特性をいいます。したがって,比較的ゆっくりな制御を行う発電機の動特性や変圧器タップ等の機器を対象とします。
2.定態安定度のメカニズム
送電電圧を\( \ V_{\mathrm {s}} \ \mathrm {[V]} \ \),受電電圧を\( \ V_{\mathrm {r}} \ \mathrm {[V]} \ \),送電線のリアクタンスを\( \ X \ [\Omega ] \ \),\( \ V_{\mathrm {s}} \ \)と\( \ V_{\mathrm {r}} \ \)の負荷角を\( \ \delta \ \)とすると,送電電力\( \ P \ \)は,
\[
\begin{eqnarray}
P&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta \\[ 5pt ]
\end{eqnarray}
\]
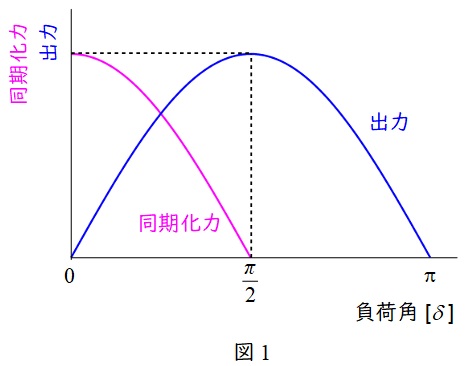
で表され,同期化力\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta } \ \)は,
\[
\begin{eqnarray}
\frac {\mathrm {d}P}{\mathrm {d}\delta }&=&\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\cos \delta \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ \displaystyle \frac {\mathrm {d}P}{\mathrm {d}\delta } > 0 \ \)の時,発電機は安定となり,\( \ \displaystyle \delta =\frac {\pi}{2} \ \)の時安定限界となります。
したがって,定態安定度を上げるには電圧階級を上げる,送電線のリアクタンスを下げる,負荷角を小さくする,等の方法があることがわかります。
3.等面積法による過渡安定度のメカニズム
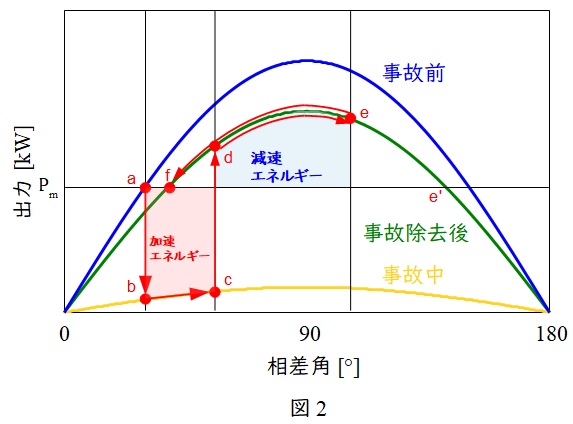
過渡安定度のメカニズムの説明には,送電電力\( \ P \ \)と相差角\( \ \delta \ \)の関係\( \ \left( \displaystyle P=\frac {V_{\mathrm {s}}V_{\mathrm {r}}}{X}\sin \delta \right) \ \)を表す図2のような\( \ P-\delta \ \)曲線による等面積法が用いられます。
図2の\( \ \mathrm {a} \ \)で安定運転していた発電機が事故が発生すると,多量の無効電力が流れ,\( \ \mathrm {b} \ \)点に移動します。事故を除去する\( \ \mathrm {c} \ \)点まで発電機は加速し,事故除去後,線路は一相分なくなる分事故前よりリアクタンスが大きくなるため,\( \ P-\delta \ \)曲線は緑線になり,\( \ \mathrm {d} \ \)点に移動します。その後,発電機は減速エネルギーが働き始め,\( \ \mathrm {e} \ \)点まで進むと減速を開始し,元の出力と同じ\( \ \mathrm {f} \ \)点まで行くと発電機は安定します。減速エネルギーが足りず,\( \ \mathrm {e}^{\prime } \ \)点まで行ってしまうと脱調します。
【解答】
(1)解答:ト
題意より解答候補は,(イ)持続,(ロ)短時間,(ヘ)応動,(ト)定態,(ル)過渡,(ワ)動態,(カ)長時間,(ソ)瞬時,になると思います。
ワンポイント解説「1.安定度の種類」の通り,ごく微小なじょう乱が加わったときの安定度は定態安定度となります。
(2)解答:ル
題意より解答候補は,(イ)持続,(ロ)短時間,(ヘ)応動,(ト)定態,(ル)過渡,(ワ)動態,(カ)長時間,(ソ)瞬時,になると思います。
ワンポイント解説「1.安定度の種類」の通り,じょう乱が比較的大きい場合で,じょう乱からの経過時間がごく短い領域の安定度は過渡安定度となります。
(3)解答:ワ
題意より解答候補は,(イ)持続,(ロ)短時間,(ヘ)応動,(ト)定態,(ル)過渡,(ワ)動態,(カ)長時間,(ソ)瞬時,になると思います。
ワンポイント解説「1.安定度の種類」の通り,励磁系や調速系などが重要な役割を持つ安定度は動態安定度となります。
(4)解答:カ
題意より解答候補は,(イ)持続,(ロ)短時間,(ヘ)応動,(ト)定態,(ル)過渡,(ワ)動態,(カ)長時間,(ソ)瞬時,になると思います。
ワンポイント解説「1.安定度の種類」の通り,電圧安定性や周波数変動といった長時間の領域の動特性は長時間動特性と呼ばれます。
(5)解答:ホ
題意より解答候補は,(ニ)分路リアクトル,(ホ)直列コンデンサ,(ヨ)並列コンデンサ,になると思います。ワンポイント解説「2.定態安定度のメカニズム」の通り,定態安定度の向上対策としては送電線のリアクタンスを小さくする直列コンデンサが効果的ですが,共振現象の発生する恐れからほとんど採用されません。
並列コンデンサは力率調整を行うときに投入します。
(6)解答:ネ
題意より解答候補は,(ハ)磁気飽和共振周波数,(レ)励磁制御系の共振周波数,(ネ)軸ねじり共振周波数,になると思います。
直列コンデンサで問題となるのは,送電系統の共振周波数と発電機の軸ねじり共振周波数とで低周波共振を発生する可能性があることとなります。
軸ねじれ現象は平成25年問6でも扱っているので,確認しておいても良いと思います。
(7)解答:ヌ
題意より解答候補は,(ヌ)\( \ \mathrm {HVDC} \ \)送電,(ヲ)ガバナ・フリー運転,(タ)\( \ \mathrm {TBC} \ \),になると思います。
安定度の対策としては安定度の問題がない直流送電(\( \ \mathrm {HVDC} \ \)送電)が効果的となります。
ガバナ・フリー運転はガバナ(調速機)で通常の負荷変動に対する周波数変動に対応するために出力を調整する運転方式で,\( \ \mathrm {TBC} \ \)は周波数バイアス連系線電力制御の略称で,多くの電力会社(東京,北海道,沖縄以外)が採用している運転制御方式です。
(8)解答:リ
題意より解答候補は,(ヘ)応動,(リ)慣性定数,等になると思います。
不安定に至るまでの時間を延ばす方法としては,発電機の慣性定数(できるだけ同じ状態を保持しようとする大きさ)を大きくすることが効果的となります。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん