【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,工場の負荷率向上に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選びなさい。
ただし,省エネルギー率とは負荷の消費電力が仮に\( \ 50 \ \mathrm {kW} \ \)から\( \ 45 \ \mathrm {kW} \ \)に減少した場合は\( \ 10 \ % \ \)とする。また負荷率の上昇分とは,仮に負荷率が\( \ 60 \ % \ \)から\( \ 65 \ % \ \)に上昇した場合は\( \ 5 \ % \ \)とする。
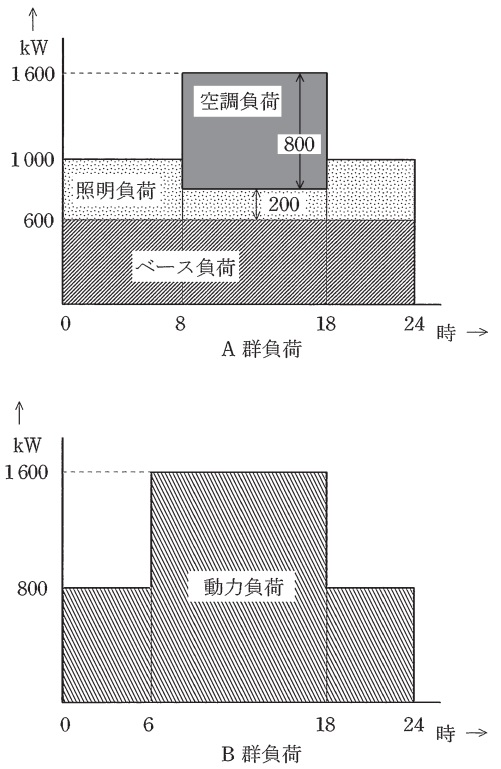
図に示すような負荷曲線を有する,\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)\( \ 2 \ \)群からなる負荷の\( \ 24 \ \)時間稼働工場がある。\( \ \mathrm {A} \ \)群負荷において次の項目の省エネルギーを実施する。
① アモルファス変圧器などを導入することにより,ベース負荷部分で\( \ 5 \ % \ \)の省エネルギー率を達成。
② 発光素子に半導体を用いた\( \ \fbox { (1) } \ \)に切り替えることにより,照明負荷部分で\( \ 60 \ % \ \)の省エネルギー率を達成。
③ 空調負荷部分は高効率ヒートポンプを導入し,\( \ \mathrm {COP} \ \)(\( \ \fbox { (2) } \ \))を\( \ 2.0 \ \)から\( \ 4.0 \ \)に改善。
\( \ \mathrm {A} \ \)群負荷の空調負荷部分はヒートポンプの補機他の動力を無視して,\( \ \mathrm {COP} \ \)のみの改善により消費電力は\( \ \fbox { (3) } \ \mathrm {kW} \ \)となる。\( \ \mathrm {A} \ \)群負荷において上記に示された全ての省エネルギー機器の導入による日負荷率の上昇分は\( \ \fbox { (4) } \ % \ \)となる。
\( \ \mathrm {B} \ \)群負荷において,日負荷率を\( \ 5 \ % \ \)上昇させるために蓄電池を設置する。充電時の効率を\( \ 80 \ % \ \)とし放電時の効率を\( \ 100 \ % \ \)とした場合,必要となる蓄電池の充電時の電力量は,\( \ \fbox { (5) } \ \mathrm {kW\cdot h} \ \)となる。なお,充電,放電時間はそれぞれ\(12\)時間とし,蓄電池の入出力はそれぞれ一定とする。
\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)群負荷において上記の対策を実施した後の,\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)群を合計した工場全体の日負荷率は\( \ \fbox { (6) } \ % \ \)となる。
〔問6の解答群〕
\[
\begin{eqnarray}
&(イ)& 成績係数 &(ロ)& 8.2 &(ハ)& 75.1 \\[ 5pt ]
&(ニ)& 制御最適値 &(ホ)& 68.2 &(ヘ)& 86.5 \\[ 5pt ]
&(ト)& 費用係数 &(チ)& 1300 &(リ)& 3.4 \\[ 5pt ]
&(ヌ)& 80.9 &(ル)& \mathrm {EL} &(ヲ)& \mathrm {LED} \\[ 5pt ]
&(ワ)& 1200 &(カ)& 400 &(ヨ)& 900 \\[ 5pt ]
&(タ)& 6.6 &(レ)& 200 &(ソ)& 1600 \\[ 5pt ]
&(ツ)& 4.1 &(ネ)& \mathrm {Hf} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
負荷率や成績係数の知識,文章の理解力,計算能力等総合的な能力が試される良問で,一種受験者のみでなく二種受験者の方にも挑戦して頂きたいような問題です。重要な内容を多数含んでいるのでじっくりと取り組み理解するようにして下さい。
1.需要率,不等率,負荷率
下の3つの公式は頻出の非常に重要な公式となりますので,試験直前にも再復習しておきましょう。
\[
\begin{eqnarray}
需要率&=& \frac {最大需要電力}{設備容量} \times 100 \ \mathrm {[%]} \\[ 5pt ]
不等率&=& \frac {個々の最大需要電力の合計}{全体の最大需要電力} \\[ 5pt ]
負荷率&=& \frac {平均需要電力}{最大需要電力} \times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
2.成績係数\( \ \mathrm {COP} \ \)
消費電力に対する空調能力の割合で,ヒートポンプでは一般に\( \ 3~5 \ \)程度になります。
\[
\begin{eqnarray}
\mathrm {COP}&=& \frac {空調能力}{消費電力} \\[ 5pt ]
\end{eqnarray}
\]
【解答】
(1)解答:ヲ
題意より,解答候補は(ル)\( \ \mathrm {EL} \ \),(ヲ)\( \ \mathrm {LED} \ \),(ネ)\( \ \mathrm {Hf} \ \),になると思います。今は十分に\( \ \mathrm {LED} \ \)電球が普及しているので,間違えたくない問題ですね。(有機)\( \ \mathrm {EL} \ \)は,テレビやディスプレイ等に採用されており,\( \ \mathrm {Hf} \ \)蛍光ランプはインバータを組み合わせた高効率化ランプです。
(2)解答:イ
ワンポイント解説「2.成績係数\( \ \mathrm {COP} \ \)」の通り,成績係数となります。
(3)解答:カ
ワンポイント解説「2.成績係数\( \ \mathrm {COP} \ \)」の通り,同じ空調能力を出力するので成績係数が\( \ 2 \ \)倍になると,消費電力は\( \ \displaystyle \frac {1}{2} \ \)倍になります。
したがって,\( \ \mathrm {A} \ \)群負荷の元々の消費電力\( \ P_{\mathrm {a1}} \ \)は\( \ 800 \ \mathrm {kW} \ \)であるので,ヒートポンプ導入後の消費電力\( \ P_{\mathrm {a2}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {a2}}&=& \frac {1}{2}P_{\mathrm {a1}} \\[ 5pt ]
&=& \frac {1}{2}\times 800 \\[ 5pt ]
&=& 400 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ツ
省エネルギー機器導入前の平均需要電力\( \ P_{\mathrm {avA1}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {avA1}}&=& \frac {1000\times 14+ 1600\times 10}{24} \\[ 5pt ]
&=& 1250 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であり,最大需要電力\( \ P_{\mathrm {mA1}} \ \)は\( \ 1600 \ \mathrm {kW} \ \)であるから,省エネルギー機器導入前の負荷率\({}_{\mathrm {A1}} \ \)は,
\[
\begin{eqnarray}
負荷率_{\mathrm {A1}}&=& \frac {P_{\mathrm {avA1}}}{P_{\mathrm {mA1}}}\times 100 \\[ 5pt ]
&=& \frac {1250}{1600}\times 100 \\[ 5pt ]
&=& 78.125 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
アモルファス変圧器導入後のベース負荷の大きさ\( \ P_{\mathrm {b2}} \ \)は,導入前のベース負荷の大きさ\( \ P_{\mathrm {b1}} \ \)が\( \ 600 \ \mathrm {kW} \ \),省エネルギー率が\( \ 5 \ % \ \)であるから,
\[
\begin{eqnarray}
P_{\mathrm {b2}}&=& \left( 1-0.05 \right) P_{\mathrm {b1}} \\[ 5pt ]
&=& \left( 1-0.05 \right) \times 600 \\[ 5pt ]
&=& 570 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となる。また,\( \ \mathrm {LED} \ \)導入により,照明負荷で\( \ 60 \ % \ \)の省エネルギー率を達成し,\( \ \mathrm {LED} \ \)導入前の照明負荷\( \ P_{\mathrm {l1}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {l1}}
=
\begin{cases}
200 & ( 8時から18時まで ) \\[ 5pt ]
400 & ( 18時から8時まで )
\end{cases}
\end{eqnarray}
\]
であるから,\( \ \mathrm {LED} \ \)導入後の照明負荷\( \ P_{\mathrm {l2}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {l2}}&=& \left( 1-0.6 \right) P_{\mathrm {l1}} \\[ 5pt ]
&=& \begin{cases}
80 & ( 8時から18時まで ) \\[ 5pt ]
160 & ( 18時から8時まで )
\end{cases}
\end{eqnarray}
\]
となる。よって,①~③導入後の\( \ \mathrm {A} \ \)群負荷の負荷曲線は図1のようになる。

したがって,省エネルギー機器導入後の平均需要電力\(P_{\mathrm {avA2}}\)は,
\[
\begin{eqnarray}
P_{\mathrm {avA2}}&=& \frac {730\times 14+ 1050\times 10}{24} \\[ 5pt ]
&≒& 863.33 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であり,最大需要電力\( \ P_{\mathrm {mA2}} \ \)は\( \ 1050 \ \mathrm {kW} \ \)であるから,省エネルギー機器導入後の負荷率\({}_{\mathrm {A2}} \ \)は,
\[
\begin{eqnarray}
負荷率_{\mathrm {A2}}&=& \frac {P_{\mathrm {avA2}}}{P_{\mathrm {mA2}}}\times 100 \\[ 5pt ]
&=& \frac {863.33}{1050}\times 100 \\[ 5pt ]
&≒& 82.222 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって負荷率の変化量は,
\[
\begin{eqnarray}
負荷率_{\mathrm {A2}}-負荷率_{\mathrm {A1}}&=& 82.222-78.125 \\[ 5pt ]
&=& 4.097 → 4.1 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:チ
蓄電池設置前の平均需要電力\( \ P_{\mathrm {avB1}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {avB1}}&=& \frac {800\times 12+ 1600\times 12}{24} \\[ 5pt ]
&=& 1200 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
であり,最大需要電力\( \ P_{\mathrm {mB1}} \ \)は\( \ 1600 \ \mathrm {kW} \ \)であるから,蓄電池設置前の負荷率\({}_{\mathrm {B1}} \ \)は,
\[
\begin{eqnarray}
負荷率_{\mathrm {B1}}&=& \frac {P_{\mathrm {avB1}}}{P_{\mathrm {mB1}}}\times 100 \\[ 5pt ]
&=& \frac {1200}{1600}\times 100 \\[ 5pt ]
&=& 75 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって蓄電池設置後の負荷率は\( \ 80 \ % \ \)となる。\( \ 6 \ \)時から\( \ 18 \ \)時の間蓄電池から供給される電力を\( \ X \ \mathrm {[kW]} \ \)とすると,\( \ 18 \ \)時から\( \ 6 \ \)時の間充電するのに必要な電力は,効率が\( \ 80 \ % \ \)であるから,
\[
\begin{eqnarray}
\frac {X}{0.8}&=& 1.25X \\[ 5pt ]
\end{eqnarray}
\]
となるので,蓄電池設置後の負荷曲線は図2のようになる。
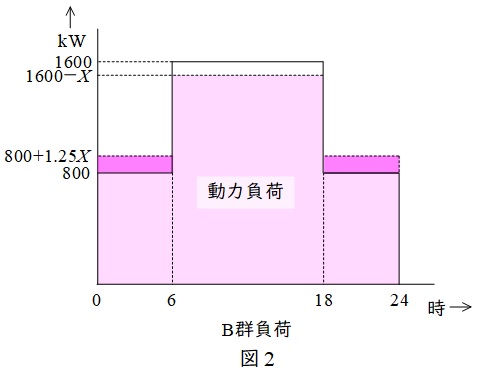
図2より,蓄電池設置後の平均需要電力\( \ P_{\mathrm {avB2}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {avB2}}&=& \frac {\left( 800+1.25X\right) \times 12+ \left( 1600-X \right) \times 12}{24} \\[ 5pt ]
&=& 1200+0.125X \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となり,その時の負荷率が\(80 \ %\)であるので,
\[
\begin{eqnarray}
\frac {1200+0.125X}{1600-X}\times 100&=& 80 \\[ 5pt ]
1200+0.125X&=& 1280-0.8X \\[ 5pt ]
X&=& 86.486 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。よって,充電時必要となる電力量\( \ W_{\mathrm {c}} \ \)は,
\[
\begin{eqnarray}
W_{\mathrm {c}}&=& 1.25X\times 12 \\[ 5pt ]
&=& 1.25\times 86.486\times 12 \\[ 5pt ]
&≒& 1297.3 → 1300 \ \mathrm {[kW\cdot h]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)解答:ヌ
\( \ \mathrm {B} \ \)群負荷において,蓄電池設置後の平均需要電力\( \ P_{\mathrm {avB2}} \ \)及び最大需要電力\( \ P_{\mathrm {mB2}} \ \)は,
\[
\begin{eqnarray}
P_{\mathrm {avB2}}&=& 1200+0.125X \\[ 5pt ]
&=& 1200+0.125\times 86.486 \\[ 5pt ]
&≒& 1210.8 \ \mathrm {[kW]} \\[ 5pt ]
P_{\mathrm {mB2}}&=& 1600-X \\[ 5pt ]
&=& 1600-86.486 \\[ 5pt ]
&≒& 1513.5 \ \mathrm {[kW]} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ \mathrm {A} \ \),\( \ \mathrm {B} \ \)群を合計した工場全体の日負荷率\({}_{\mathrm {AB}} \ \)は,
\[
\begin{eqnarray}
日負荷率_{\mathrm {AB}}&=& \frac {P_{\mathrm {avA2}}+P_{\mathrm {avB2}}}{P_{\mathrm {mA2}}+P_{\mathrm {mB2}}}\times 100 \\[ 5pt ]
&=& \frac {863.33+1210.8}{1050+1513.5}\times 100 \\[ 5pt ]
&≒& 80.910 → 80.9 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん