《機械》〈電熱〉[H30:問4]熱電素子における物質の接合界面で吸熱や放熱に関する空欄穴埋問題

【問題】

【難易度】★★★☆☆（普通）

次の文章は，熱電素子に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる最も適切なものを解答群の中から選べ。

熱電素子は異なる\( \ 2 \ \)種類の物質を接続して構成されている。熱電素子に電流を流すと，物質の接合界面で吸熱や放熱が起こる。これを\( \ \fbox {　 （１） 　} \ \)といい，静止形のヒートポンプとして利用することができる。熱電素子は半導体製造，光通信，バイオ・医療などの分野において，温度調節や冷却などの目的に広く使われている。民生部門では，小形の保冷庫や冷蔵庫などにも用いられている。

熱電素子は，電流方向の切換えによって，一つの素子で加熱と冷却の両方が行えるため，フィードバック制御によって精密な温度制御が可能である。\( \ \fbox {　 （１） 　} \ \)による吸熱量は，二種類の物質の\( \ \fbox {　 （２） 　} \ \)をそれぞれ\( \ S_{\mathrm {A}} \ \)，\( \ S_{\mathrm {B}} \ \)とすると，\( \ \fbox {　 （３） 　} \ \)に比例する。この吸熱量のほかに，素子で発生するジュール熱，素子の熱コンダクタンス，吸熱面と放熱面との温度差などによって，熱電素子としての熱輸送量が決まる。吸熱面と放熱面との温度差を一定にして，大きな熱輸送量を得るために，複数の熱電素子を\( \ \fbox {　 （４） 　} \ \)に接続し，一つのモジュールを構成している。吸熱面と放熱面との温度差を大きくとりたい場合には，このようなモジュールを多段に積み重ねる。

また，熱電素子の性能を表す指数の一つに成績係数(熱電素子の消費電力に対する吸熱量及び放熱量の割合)がある。冷却の成績係数の値は加熱の場合より\( \ \fbox {　 （５） 　} \ \)だけ小さい。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　ペルチェ効果　　　　　　　　&（ロ）&　1 \\[ 5pt ] &（ハ）&　S_{\mathrm {A}}-S_{\mathrm {B}}　　　　　　　　&（ニ）&　ジュール・トムソン効果 \\[ 5pt ] &（ホ）&　吸収係数　　　　　　　　&（ヘ）&　プラントル数 \\[ 5pt ] &（ト）&　ゼーベック効果　　　　　　　　&（チ）&　2 \\[ 5pt ] &（リ）&　熱的に直列　　　　　　　　&（ヌ）&　熱的に並列 \\[ 5pt ] &（ル）&　\frac {S_{\mathrm {A}}+S_{\mathrm {B}}}{2}　　　　　　　　&（ヲ）&　S_{\mathrm {A}}+S_{\mathrm {B}} \\[ 5pt ] &（ワ）&　ゼーベック係数　　　　　　　　&（カ）&　0.5 \\[ 5pt ] &（ヨ）&　1.5 \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ペルチェ効果やゼーベック効果は理論科目の出題範囲になりますが，ヒートポンプに利用するということで機械科目に出題されています。ペルチェ効果が電流から発熱・吸熱するのに対し，ゼーベック効果が温度差から起電力を生じる逆の現象であるため，セットで覚えておくと良いと思います。ヒートポンプの成績係数に関しては二種の問題で扱われていますので，もしわからなければ復習しておいて下さい。

1.ペルチェ効果
異なる金属や半導体を接合して，電圧をかけると，吸熱もしくは発熱を発生する現象です。図1が代表的な半導体を使用したペルチェ素子で，電流の向きを逆にすると，発熱と吸熱も入れ替わります。

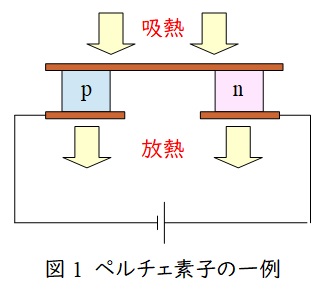
2.ゼーベック効果
異なる金属や半導体を図2のように接合して閉回路を作り，一端を高温（温接点），もう一端を低温（冷接点）とすると，熱起電力が発生し電流が流れる現象を言います。

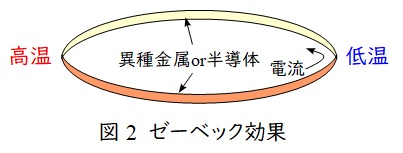
【解答】

(1)解答：イ
題意より，解答候補は（イ）ペルチェ効果，（ニ）ジュール・トムソン効果，（ト）ゼーベック効果，となると思います。ワンポイント解説「1.ペルチェ効果」の通り，問題文はペルチェ効果そのものの説明となります。

(2)解答：ワ
題意より，解答候補は（ホ）吸収係数，（ヘ）プラントル数，（ワ）ゼーベック係数，となると思います。ペルチェ効果に対する係数ペルチェ係数も見たことがある気がしますが，ここでは選択肢にないため，ゼーベック係数が適当と思います。

(3)解答：ハ
題意より，解答候補は（ハ）\(S_{\mathrm {A}}-S_{\mathrm {B}}\)，（ル）\(\displaystyle \frac {S_{\mathrm {A}}+S_{\mathrm {B}}}{2}\)，（ヲ）\(S_{\mathrm {A}}+S_{\mathrm {B}}\)，となると思います。ゼーベック係数は感覚的には金属や半導体の電流の流れやすさの指標のようなものなので，それぞれの流れやすさの差で電流が決まります。

(4)解答：ヌ
題意より，解答候補は（リ）熱的に直列，（ヌ）熱的に並列，となると思います。大きな輸送量を得るためには図3のように接続します。これを熱的に並列と呼びます。

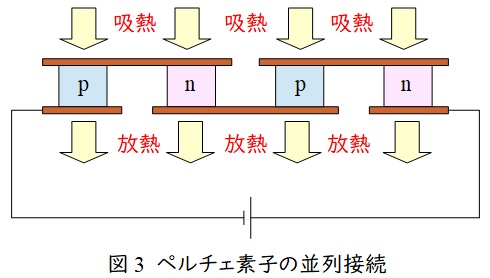
(5)解答：ロ
題意より，解答候補は（ロ）\(1\)，（チ）\(2\)，（カ）\(0.5\)，（ヨ）\(1.5\)，となると思います。ヒートポンプにおいて，蒸発器の吸熱量\(Q_{\mathrm {L}}\)及び圧縮機にかける仕事量\(W\)，凝縮器の放熱量\(Q_{\mathrm {H}}\)とすると，
\[
\begin{eqnarray}
Q_{\mathrm {H}}&=&Q_{\mathrm {L}}+W \\[ 5pt ] \end{eqnarray}
\] という関係があり，冷房時と暖房時の成績係数\(\mathrm {{COP}_{L}}\)，\(\mathrm {{COP}_{H}}\)は，
\[
\begin{eqnarray}
\mathrm {{COP}_{L}}&=&\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ] \mathrm {{COP}_{H}}&=&\frac {Q_{\mathrm {H}}}{W} \\[ 5pt ] &=&\frac {Q_{\mathrm {L}}+W}{W} \\[ 5pt ] &=&1+\frac {Q_{\mathrm {L}}}{W} \\[ 5pt ] \end{eqnarray}
\] となります。よって，冷却の成績係数は加熱の場合より\( \ 1 \ \)だけ小さくなります。