《機械・制御》〈誘導機〉[H20:問1]二重かご形誘導電動機に発生するトルクに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★☆☆☆☆（易しい）

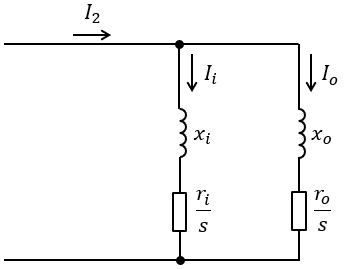
定格周波数\( \ 60 \ \mathrm {[Hz]} \ \)，\( \ 4 \ \)極の三相二重かご形誘導電動機がある。この電動機の回転子の一相分の等価回路は近似的に図のように示される。

この図で，\( \ I \ \)は電流，\( \ r \ \)は抵抗，\( \ x \ \)はリアクタンス，\( \ s \ \)は滑り，添え字の\( \ i \ \)は内かご，\( \ o \ \)は外かご，\( \ 2 \ \)は回転子回路（二次回路）を示す。

この電動機が静止しているときの内かごのインピーダンス\( \ {\dot Z}_{i} \ \mathrm {[\Omega ]} \ \)及び外かごのインピーダンス\( \ {\dot Z}_{o} \ \mathrm {[\Omega ]} \ \)は次式で表される。
\[
\begin{eqnarray}
{\dot Z}_{i} &=& 0.03+j3 \ \mathrm {[\Omega ]} \\[ 5pt ] {\dot Z}_{o} &=& 0.3+j2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] この電動機を\( \ 3 \ \mathrm {[％]} \ \)の滑りで運転しているとき，図の等価回路における回転子の一相当たりの電圧（相電圧）は\( \ 56 \ \mathrm {[V]} \ \)である。この運転条件で運転しているときの電動機について，次の値を求めよ。

　(1)　内かごのインピーダンス\( \ {\dot Z}_{is} \ \mathrm {[\Omega ]} \ \)（複素数）及び外かごのインピーダンス\( \ {\dot Z}_{os} \ \mathrm {[\Omega ]} \ \)（複素数）

　(2)　回転子回路の合成インピーダンス\( \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ \)（複素数）

　(3)　二次電流\( \ I_{2} \ \mathrm {[A]} \ \)

　(4)　発生トルク\( \ T \ \mathrm {[N\cdot m]} \ \)

【ワンポイント解説】

与えられた等価回路を用いて誘導電動機の発生トルクを求める問題です。
内かごと外かごが分かれた等価回路を用いた問題ですが，内容は電気回路の計算と基礎的な誘導機の計算となっています。計算間違いに注意して完答を目指すようにして下さい。

1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)
三相誘導電動機の極数が\( \ p \ \)，電源の周波数が\( \ f \ \mathrm {[Hz]} \ \)の時，同期速度\( \ N_{\mathrm {s}} \ \mathrm {[{min}^{-1}]} \ \)は，
\[
\begin{eqnarray}
N_{\mathrm {s}} &=&\frac {120f}{p} \\[ 5pt ] \end{eqnarray}
\] となります。また，同期角速度\( \ \omega _{\mathrm {s}} \ \mathrm {[rad / s]} \ \)は，
\[
\begin{eqnarray}
\omega _{\mathrm {s}} &=&\frac {2\pi N_{\mathrm {s}}}{60} \\[ 5pt ] &=&\frac {2\pi }{60}\cdot \frac {120f}{p} \\[ 5pt ] &=&\frac {4\pi f}{p} \\[ 5pt ] \end{eqnarray}
\] で求められます。

2.誘導機の滑り\( \ s \ \)
誘導機の同期速度が\( \ N_{\mathrm {s}} \ \mathrm {[{min} ^{-1}]} \ \)，回転速度が\( \ N \ \mathrm {[{min} ^{-1}]} \ \)である時，誘導機の滑り\( \ s \ \)は，
\[
\begin{eqnarray}
s &=&\frac {N_{\mathrm {s}}-N}{N_{\mathrm {s}}} \\[ 5pt ] \end{eqnarray}
\] と定義されるので，\( \ N \ \)について整理すると，
\[
\begin{eqnarray}
s N_{\mathrm {s}}&=&N_{\mathrm {s}}-N \\[ 5pt ] N&=&\left( 1-s\right) N_{\mathrm {s}} \\[ 5pt ] \end{eqnarray}
\] となります。

3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係
誘導電動機の\( \ \mathrm {L} \ \)形等価回路は図1のようになります。図1において，\( \ {\dot V}_{1} \ \mathrm {[V]} \ \)は一次側端子電圧，\( \ {\dot I}_{1} \ \mathrm {[A]} \ \)は一次電流，\( \ {\dot I}_{2}^{\prime } \ \mathrm {[A]} \ \)は二次電流の一次換算，\( \ {\dot I}_{0} \ \mathrm {[A]} \ \)は励磁電流，\( \ r_{1} \ \mathrm {[\Omega ]} \ \)は一次巻線抵抗，\( \ r_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次巻線抵抗の一次換算，\( \ x_{1} \ \mathrm {[\Omega ]} \ \)は一次漏れリアクタンス，\( \ x_{2}^{\prime } \ \mathrm {[\Omega ]} \ \)は二次漏れリアクタンスの一次換算，\( \ s \ \)は滑りとなります。
図1より，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)，二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は，
\[
\begin{eqnarray}
P_{\mathrm {o}} &=& 3\frac {1-s}{s}r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] P_{\mathrm {c2}} &=& 3r_{2}^{\prime }{I_{2}^{\prime }}^{2} \\[ 5pt ] P_{2} &=& P_{\mathrm {o}}+P_{\mathrm {c2}} =3\frac {r_{2}^{\prime }}{s}{I_{2}^{\prime }}^{2} \\[ 5pt ] \end{eqnarray}
\] となり，誘導電動機の二次入力\( \ P_{2} \ \mathrm {[W]} \ \)，出力\( \ P_{\mathrm {o}} \ \mathrm {[W]} \ \)，二次銅損\( \ P_{\mathrm {c2}} \ \mathrm {[W]} \ \)には，
\[
\begin{eqnarray}
P_{2}：P_{\mathrm {o}}：P_{\mathrm {c2}} &=& 1：(1-s)：s \\[ 5pt ] \end{eqnarray}
\] の関係があることが分かります。

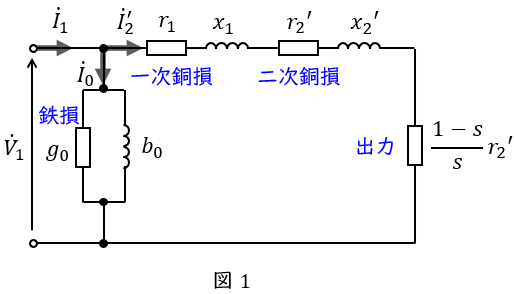
4.誘導電動機のトルク
図1より，三相誘導電動機のトルク\( \ T \ \)は，
\[
\begin{eqnarray}
T &=&\frac {P_{\mathrm {o}}}{\omega } \\[ 5pt ] &=&\frac {P_{\mathrm {2}}\left( 1-s\right) }{\omega _{\mathrm {s}}\left( 1-s\right) } \\[ 5pt ] &=&\frac {P_{\mathrm {2}}}{\omega _{\mathrm {s}}} \\[ 5pt ] &=& \frac {1}{\omega _{\mathrm {s}}}\frac {3V_{1}^{2}\displaystyle \frac {r_{2}^{\prime }}{s}}{\left( r_{1}+\displaystyle \frac {r_{2}^{\prime }}{s}\right) ^{2}+\left( x_{1}+x_{2}^{\prime }\right) ^{2}} \\[ 5pt ] \end{eqnarray}
\] で求められます。

【解答】

(1)内かごのインピーダンス\( \ {\dot Z}_{is} \ \mathrm {[\Omega ]} \ \)（複素数）及び外かごのインピーダンス\( \ {\dot Z}_{os} \ \mathrm {[\Omega ]} \ \)（複素数）
問題図の等価回路より，内かごのインピーダンス\( \ {\dot Z}_{is} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
{\dot Z}_{is} &=&\frac {r_{i}}{s}+jx_{i} \\[ 5pt ] &=&\frac {0.03}{0.03}+j3 \\[ 5pt ] &=&1+j3 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] となり，同様に外かごのインピーダンス\( \ {\dot Z}_{os} \ \mathrm {[\Omega ]} \ \)は，
\[
\begin{eqnarray}
{\dot Z}_{os} &=&\frac {r_{o}}{s}+jx_{o} \\[ 5pt ] &=&\frac {0.3}{0.03}+j2 \\[ 5pt ] &=&10+j2 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)回転子回路の合成インピーダンス\( \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ \)（複素数）
回転子回路の合成インピーダンス\( \ {\dot Z}_{2} \ \mathrm {[\Omega ]} \ \)は，\( \ {\dot Z}_{is} \ \mathrm {[\Omega ]} \ \)と\( \ {\dot Z}_{os} \ \mathrm {[\Omega ]} \ \)の並列合成インピーダンスであるから，
\[
\begin{eqnarray}
{\dot Z}_{2} &=&\frac {{\dot Z}_{is}{\dot Z}_{os}}{{\dot Z}_{is}+{\dot Z}_{os}} \\[ 5pt ] &=&\frac {\left( 1+j3\right) \left( 10+j2\right) }{\left( 1+j3\right) +\left( 10+j2\right) } \\[ 5pt ] &=&\frac {10+j2+j30-6}{11+j5} \\[ 5pt ] &=&\frac {4+j32}{11+j5}\times \frac {11-j5}{11-j5} \\[ 5pt ] &=&\frac {44-j20+j352+160}{121+25} \\[ 5pt ] &=&\frac {204+j332}{146} \\[ 5pt ] &≒&1.397 \ 3+j2.274 \ 0　→　1.40+j2.27 \ \mathrm {[\Omega ]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)二次電流\( \ I_{2} \ \mathrm {[A]} \ \)
二次電流\( \ I_{2} \ \mathrm {[A]} \ \)は，回転子の一相当たりの電圧（相電圧）が\( \ E_{2}=56 \ \mathrm {[V]} \ \)であるから，
\[
\begin{eqnarray}
I_{2} &=&\frac {E_{2}}{Z_{2}} \\[ 5pt ] &=&\frac {56}{\sqrt {1.397 \ 3^{2}+2.274 \ 0^{2}}} \\[ 5pt ] &≒&20.982　→　21.0 \ \mathrm {[A]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)発生トルク\( \ T \ \mathrm {[N\cdot m]} \ \)
二次入力\( \ P_{2} \ \mathrm {[W]} \ \)は，ワンポイント解説「3.二次入力\( \ P_{2} \ \)と出力\( \ P_{\mathrm {o}} \ \)と二次銅損\( \ P_{\mathrm {c2}} \ \)の関係」の通り，
\[
\begin{eqnarray}
P_{2} &=&3r_{2}{I_{2}}^{2} \\[ 5pt ] &=&3\times 1.397 \ 3 \times 20.982^{2} \\[ 5pt ] &≒&1 \ 845.5 \ \mathrm {[W]} \\[ 5pt ] \end{eqnarray}
\] であり，同期角速度\( \ \omega _{s} \ \mathrm {[rad / s]} \ \)は，ワンポイント解説「1.三相誘導電動機の同期速度\( \ N_{\mathrm {s}} \ \)及び同期角速度\( \ \omega _{\mathrm {s}} \ \)」の通り，
\[
\begin{eqnarray}
\omega _{s} &=&\frac {4\pi f}{p} \\[ 5pt ] &=&\frac {4\pi \times 60}{4} \\[ 5pt ] &≒&188.50 \ \mathrm {[rad / s]} \\[ 5pt ] \end{eqnarray}
\] であるので，トルク\( \ T \ \mathrm {[N\cdot m]} \ \)は，ワンポイント解説「4.誘導電動機のトルク」の通り，
\[
\begin{eqnarray}
T &=&\frac {P_{2}}{\omega _{s}} \\[ 5pt ] &=&\frac {1 \ 845.5}{188.50} \\[ 5pt ] &≒&9.79 \ \mathrm {[N\cdot m]} \\[ 5pt ] \end{eqnarray}
\] と求められる。