【問題】
【難易度】★★★★☆(やや難しい)
変圧器の一次巻線の基準タップに電圧を加えたときの二次端子の電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)は,\( \ \mathrm {IEC} \ \)(国際電気標準会議)での定義によると次の値である。すなわち,変圧器を無負荷として一次巻線の基準タップに定格一次電圧を加え,二次電圧を定格二次電圧\( \ V_{\mathrm {N}} \ \)とする。次に一次電圧を定格電圧に保ったまま指定の負荷及び力率としたときの二次電圧\( \ V_{\mathrm {L}} \ \)を求める。\( \ \varepsilon \ \mathrm {[%]} \ \)は,次の値である。
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{\mathrm {N}}-V_{\mathrm {L}}}{V_{\mathrm {N}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
この定義に従って電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)に関する次の問に答えよ。ただし,電圧,電流,インピーダンスなどは,変圧器の定格電圧及び定格容量を基準とした百分率で表す。
(1) 百分率抵抗降下\( \ p=0.5 \ \mathrm {[%]} \ \)及び百分率リアクタンス降下\( \ q=10 \ \mathrm {[%]} \ \)の変圧器の二次端子に力率が\( \ 0.8 \ \)(遅れ)で大きさが\( \ 100 \ \mathrm {[%]} \ \)の負荷インピーダンスを接続したときの電圧変動率を求めよ。
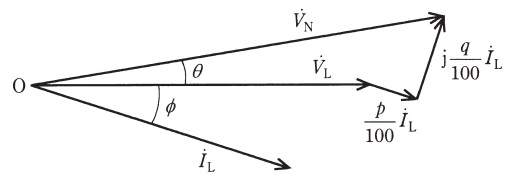
(2) 百分率抵抗降下\( \ p \ \mathrm {[%]} \ \)及び百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)の変圧器に力率が\( \ \cos \phi \ \)(遅れ)で大きさが\( \ I_{\mathrm {L}} \ \mathrm {[%]} \ \)の二次電流を通電したときの電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)を\( \ I_{\mathrm {L}} \ \),\( \ p \ \),\( \ q \ \)及び\( \ \phi \ \)を用いた式で求めよ。ここで,\( \ {\dot V}_{\mathrm {L}} \ \)を基準としてフェーザで表したとき,無負荷時の二次電圧\( \ {\dot V}_{\mathrm {N}} \ \),及び二次電流\( \ {\dot I}_{\mathrm {L}} \ \)は,次の図の関係があること,\( \ {\dot V}_{\mathrm {N}} \ \)の大きさは\( \ 100 \ \mathrm {[%]} \ \)であること,並びに\( \ \cos \theta =\sqrt {1-\sin ^{2}\theta } \ \)であることを考慮する。なお,\( \ \theta \ \)は\( \ {\dot V}_{\mathrm {L}} \ \)に対する\( \ {\dot V}_{\mathrm {N}} \ \)の位相角である。
(3) \( \ x^{2}≪1 \ \)のとき,次の近似式が成り立つ。
\[
\begin{eqnarray}
\sqrt {1-x^{2}} &≒&1-\frac {x^{2}}{2} \\[ 5pt ]
\end{eqnarray}
\]
この近似式を用いて上記(2)で得た式の近似式を求めよ。
【ワンポイント解説】
変圧器の電圧変動率に関する問題ですが,ほとんど数値計算に関する問題と言えると思います。
機械制御の制限時間から考えると本問を\( \ 30 \ \)分で解くのは非常に厳しいかと思いますが,電圧変動率の近似式を導出する練習問題としてとても勉強になる問題と言えると思います。
1.変圧器の電圧変動率\( \ \varepsilon \ \)
変圧器の電圧変動率\( \ \varepsilon \ \)は,図1-1のように二次側を無負荷(開放)として一次側に定格一次電圧を加えたときの二次側端子電圧を\( \ V_{20} \ \mathrm {[V]} \ \),図1-2のように二次側を定格負荷として一次側に定格一次電圧を加えたときの二次側端子電圧を\( \ V_{\mathrm {2n}} \ \mathrm {[V]} \ \)としたとき,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
で定義されます。
※ 本問においては無負荷時の電圧を分母においており,上記と異なるので注意して下さい。
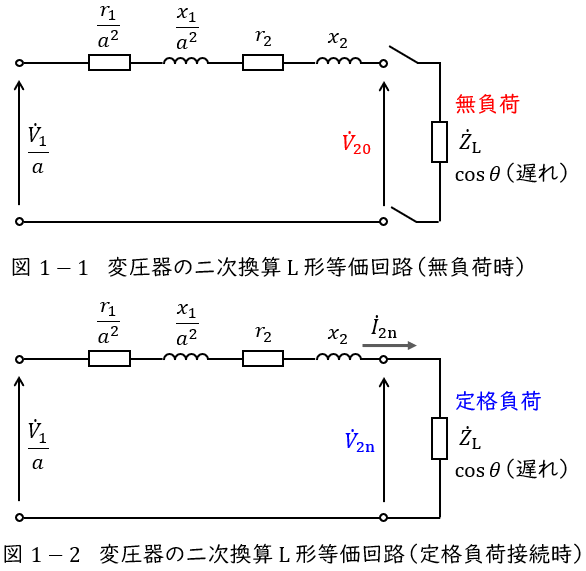
2.百分率抵抗降下\( \ p \ \)と百分率リアクタンス降下\( \ q \ \)
変圧器の一次二次を合算した抵抗成分を\( \ R=\displaystyle \frac {r_{1}}{a^{2}}+r_{2} \ \),一次二次を合算したリアクタンス成分を\( \ X=\displaystyle \frac {x_{1}}{a^{2}}+x_{2} \ \)とし,定格二次電圧を\( \ V_{\mathrm {2n}} \ \mathrm {[V]} \ \),定格二次電流を\( \ I_{\mathrm {2n}} \ \mathrm {[A]} \ \)とすると,百分率抵抗降下\( \ p \ \mathrm {[%]} \ \)及び百分率リアクタンス降下\( \ q \ \mathrm {[%]} \ \)は,
\[
\begin{eqnarray}
p &=&\frac {RI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
q &=&\frac {XI_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となります。
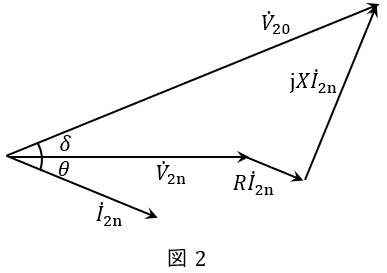
定格負荷(遅れ力率\( \ \cos \theta \ \))を接続したときの変圧器のベクトル図は図2のように描くことができ,電圧変動率\( \ \varepsilon \ \)は上記\( \ p \ \),\( \ q \ \)を用いると,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{20}-V_{\mathrm {2n}}}{V_{\mathrm {2n}}}\times 100 \\[ 5pt ]
&≃&p\cos \theta + q\sin \theta +\frac {1}{200}\left( q\cos \theta -p\sin \theta \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と近似することができ,\( \ {\dot V}_{\mathrm {20}} \ \)と\( \ {\dot V}_{\mathrm {2n}} \ \)の位相差が十分に小さく,\( \ \varepsilon \ \)が\( \ 4 % \ \)以下の場合には,
\[
\begin{eqnarray}
\varepsilon &≃&p\cos \theta + q\sin \theta \\[ 5pt ]
\end{eqnarray}
\]
と近似することができます。
【解答】
(1)百分率抵抗降下\( \ p=0.5 \ \mathrm {[%]} \ \)及び百分率リアクタンス降下\( \ q=10 \ \mathrm {[%]} \ \)の変圧器の二次端子に力率が\( \ 0.8 \ \)(遅れ)で大きさが\( \ 100 \ \mathrm {[%]} \ \)の負荷インピーダンスを接続したときの電圧変動率
負荷の百分率インピーダンスを\( \ {\dot Z}_{\mathrm {L}}=R_{\mathrm {L}}+\mathrm {j}X_{\mathrm {L}} \ \)とおくと,
\[
\begin{eqnarray}
R_{\mathrm {L}} &=&Z_{\mathrm {L}}\cos \theta \\[ 5pt ]
&=&100\times 0.8 \\[ 5pt ]
&=&80 \ \mathrm {[%]} \\[ 5pt ]
X_{\mathrm {L}} &=&Z_{\mathrm {L}}\sin \theta \\[ 5pt ]
&=&Z_{\mathrm {L}}\sqrt {1-\cos ^{2}\theta } \\[ 5pt ]
&=&100\times \sqrt {1-0.8^{2}} \\[ 5pt ]
&=&60 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
となるから,分圧の法則より,
\[
\begin{eqnarray}
{\dot V}_{\mathrm {L}} &=&\frac {{\dot Z}_{\mathrm {L}}}{{\dot Z}_{\mathrm {L}}+p+\mathrm {j}q}{\dot V}_{\mathrm {N}} \\[ 5pt ]
&=&\frac {R_{\mathrm {L}}+\mathrm {j}X_{\mathrm {L}}}{R_{\mathrm {L}}+\mathrm {j}X_{\mathrm {L}}+p+\mathrm {j}q}{\dot V}_{\mathrm {N}} \\[ 5pt ]
&=&\frac {R_{\mathrm {L}}+\mathrm {j}X_{\mathrm {L}}}{\left( R_{\mathrm {L}}+p\right) +\mathrm {j}\left( X_{\mathrm {L}}+q\right) }{\dot V}_{\mathrm {N}} \\[ 5pt ]
\end{eqnarray}
\]
の関係があるので,その大きさ\( \ V_{\mathrm {L}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {L}} &=&\frac {\sqrt { R_{\mathrm {L}}^{2}+X_{\mathrm {L}}^{2} }}{\sqrt {\left( R_{\mathrm {L}}+p\right) ^{2}+\left( X_{\mathrm {L}}+q\right) ^{2}}}V_{\mathrm {N}} \\[ 5pt ]
&=&\frac {\sqrt { 80^{2}+60^{2} }}{\sqrt {\left( 80+0.5\right) ^{2}+\left( 60+10\right) ^{2}}}\times V_{\mathrm {N}} \\[ 5pt ]
&=&\frac {100}{106.678}\times V_{\mathrm {N}} \\[ 5pt ]
&≒&0.93740 V_{\mathrm {N}} \\[ 5pt ]
\end{eqnarray}
\]
となる。したがって,電圧変動率\( \ \varepsilon \ \)は,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{\mathrm {N}}-V_{\mathrm {L}}}{V_{\mathrm {N}}}\times 100 \\[ 5pt ]
&=&\frac {V_{\mathrm {N}}-0.93740 V_{\mathrm {N}}}{V_{\mathrm {N}}}\times 100 \\[ 5pt ]
&=&\frac {1-0.93740}{1}\times 100 \\[ 5pt ]
&=&6.260 → 6.26 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)力率が\( \ \cos \phi \ \)(遅れ)で大きさが\( \ I_{\mathrm {L}} \ \mathrm {[%]} \ \)の二次電流を通電したときの電圧変動率\( \ \varepsilon \ \mathrm {[%]} \ \)を\( \ I_{\mathrm {L}} \ \),\( \ p \ \),\( \ q \ \)及び\( \ \phi \ \)を用いた式で表す
図3に示す三角形に三平方の定理を適用すると,
\[
\begin{eqnarray}
V_{\mathrm {N}}^{2} &=&\left( V_{\mathrm {L}}+\frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) ^{2} +\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ V_{\mathrm {L}} \ \)について整理すると,
\[
\begin{eqnarray}
\left( V_{\mathrm {L}}+\frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) ^{2} &=&V_{\mathrm {N}}^{2} -\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2} \\[ 5pt ]
V_{\mathrm {L}}+\frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi &=&\sqrt {V_{\mathrm {N}}^{2} -\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2}} \\[ 5pt ]
V_{\mathrm {L}}&=&-\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) +\sqrt {V_{\mathrm {N}}^{2} -\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
となる。これを電圧変動率の式に代入して,さらに\( \ V_{\mathrm {N}}=100 \ \mathrm {[%]} \ \)を代入すると,
\[
\begin{eqnarray}
\varepsilon &=&\frac {V_{\mathrm {N}}-V_{\mathrm {L}}}{V_{\mathrm {N}}}\times 100 \\[ 5pt ]
&=&\frac {\displaystyle V_{\mathrm {N}}-\left \{ -\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) +\sqrt {V_{\mathrm {N}}^{2} -\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2}}\right\} }{V_{\mathrm {N}}}\times 100 \\[ 5pt ]
&=&\frac {\displaystyle V_{\mathrm {N}}+\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) -\sqrt {V_{\mathrm {N}}^{2} -\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2}} }{V_{\mathrm {N}}}\times 100 \\[ 5pt ]
&=&\left\{ 1+\frac {1}{V_{\mathrm {N}}}\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) -\sqrt {1 -\frac {1}{V_{\mathrm {N}}^{2}}\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2}}\right\} \times 100 \\[ 5pt ]
&=&\left\{ 1+\frac {1}{100}\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) -\sqrt {1 -\frac {1}{100^{2}}\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2}}\right\} \times 100 \\[ 5pt ]
&=&100+\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) -100\sqrt {1 -\left\{ \frac {1}{100}\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) \right\} ^{2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
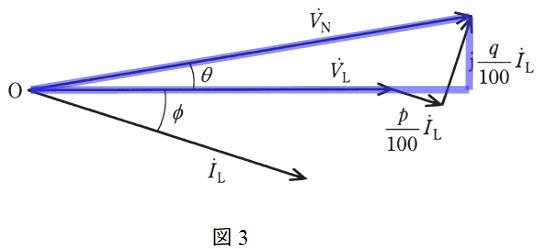
(3)(2)で得た式の近似式を求める
(2)解答式に与えられた近似式を適用すると,
\[
\begin{eqnarray}
\varepsilon &≃&100+\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) -100\left[ 1-\frac {1}{2}\left\{ \frac {1}{100}\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) \right\}^{2} \right] \\[ 5pt ]
&=&100+\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) -100+100\times \frac {1}{2}\left\{ \frac {1}{100}\left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) \right\}^{2} \\[ 5pt ]
&=&\left( \frac {p}{100}I_{\mathrm {L}}\cos \phi +\frac {q}{100}I_{\mathrm {L}}\sin \phi \right) + \frac {1}{200} \left( \frac {q}{100}I_{\mathrm {L}}\cos \phi -\frac {p}{100}I_{\mathrm {L}}\sin \phi \right) ^{2} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん