【問題】
【難易度】★★★☆☆(普通)
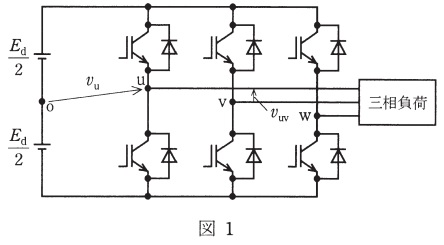
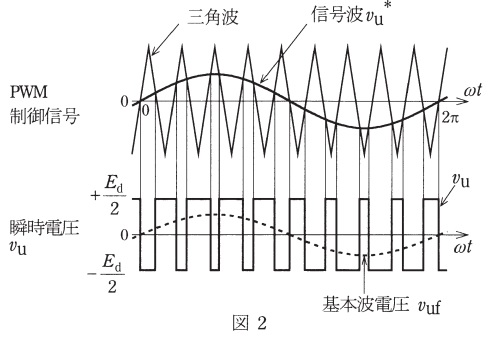
図1に示す三相電圧形インバータにおいて,\( \ \mathrm {u} \ \)相→\( \ \mathrm {v} \ \)相→\( \ \mathrm {w} \ \)相の相順で出力する相電圧(\( \ \mathrm {o} \ \)点を基準にした各出力端子との間の電圧)\( \ v_{\mathrm {u}} \ \),\( \ v_{\mathrm {v}} \ \),\( \ v_{\mathrm {w}} \ \)の制御に図2に示す三角波比較\( \ \mathrm {PWM} \ \)制御を用いる。
変調率を\( \ A=\displaystyle \frac {信号波波高値}{三角波波高値} \ \)と定義し,信号波周波数に対して三角波周波数は十分に高く,デッドタイムを無視する。図2に示す信号波\( \ {v_{\mathrm {u}}}^{*} \ \)が正弦波であれば,\( \ \mathrm {u} \ \)相の瞬時電圧\( \ v_{\mathrm {u}} \ \)には,変調率\( \ 1 \ \)以下では信号波\( \ {v_{\mathrm {u}}}^{*} \ \)に比例した基本波電圧\( \ v_{\mathrm {uf}} \ \)が含まれる。直流電圧を\( \ E_{\mathrm {d}} \ \),基本波電圧の角周波数を\( \ \omega \ \)として,次の問に答えよ。
(1) 各相\( \ \mathrm {IGBT} \ \)について,信号波と三角波とを比較して,大小がどのような関係のときに上アーム\( \ \mathrm {IGBT} \ \)及び下アーム\( \ \mathrm {IGBT} \ \)をオン又はオフするかを述べよ。
(2) 図2に示す基本波を信号波とする\( \ \mathrm {PWM} \ \)制御を方式\( \ 1 \ \)とする。この方式の瞬時出力電圧\( \ v_{\mathrm {u1}} \ \),\( \ v_{\mathrm {v1}} \ \),\( \ v_{\mathrm {w1}} \ \)に含まれる基本波電圧を\( \ v_{\mathrm {uf1}} \ \),\( \ v_{\mathrm {vf1}} \ \),\( \ v_{\mathrm {wf1}} \ \)とする。この三つの基本波電圧\( \ v_{\mathrm {uf1}} \ \),\( \ v_{\mathrm {vf1}} \ \),\( \ v_{\mathrm {wf1}} \ \)の瞬時値を,そのときの変調率\( \ A_{\mathrm {1}} \ \)及び\( \ E_{\mathrm {d}} \ \)を用いて,\( \ \sin \ \)を使った式で示せ。ただし,三角波波高値を\( \ 1 \ \)とすると,変調率\( \ A_{\mathrm {1}} \ \)の\( \ \mathrm {u} \ \)相信号波は\( \ {v_{\mathrm {u1}}}^{*}=A_{\mathrm {1}}\sin \omega t \ \)で表される。さらに\( \ A_{\mathrm {1}}=1 \ \)の場合,基本波電圧\( \ v_{\mathrm {uf1}} \ \)の波高値は,インバータで出力できる最大電圧\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \)となる。また,三相信号波\( \ v_{\mathrm {u1}}^{*} \ \),\( \ v_{\mathrm {v1}}^{*} \ \),\( \ v_{\mathrm {w1}}^{*} \ \)は三相対称であるとする。
(3) \( \ \mathrm {PWM} \ \)制御方式\( \ 1 \ \)において,\( \ A_{\mathrm {1}}=1 \ \)の場合の\( \ \mathrm {u}-\mathrm {v} \ \)相線間電圧\( \ v_{\mathrm {uv1}} \ \)の基本波実効値\( \ V_{\mathrm {uvf1}} \ \)を,\( \ E_{\mathrm {d}} \ \)を用いて示せ。
(4) 基本波に,波高値が\( \ \displaystyle \frac {1}{6} \ \)倍の\( \ 3 \ \)次高調波を加算した信号波を用いた\( \ \mathrm {PWM} \ \)制御を方式\( \ 2 \ \)とする。この方式\( \ 2 \ \)において,基本波の波高値が\( \ 1 \ \)の場合の\( \ \mathrm {u} \ \)相信号波\( \ v_{\mathrm {u2}}^{*} \ \)を次式とする。
\[
\begin{eqnarray}
v_{\mathrm {u2}}^{*} &=&\sin \omega t +\frac {1}{6}\sin 3\omega t \\[ 5pt ]
\end{eqnarray}
\]
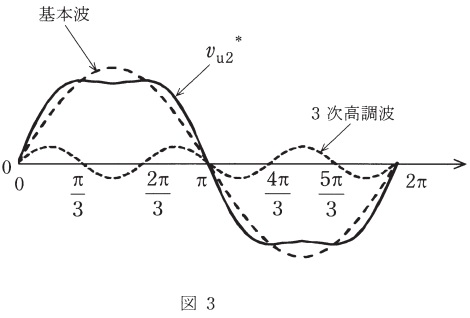
この信号波\( \ v_{\mathrm {u2}}^{*} \ \)は,図3に示すように\( \ \displaystyle \omega t=\frac {\pi }{3},\frac {2\pi }{3},\frac {4\pi }{3},\frac {5\pi }{3} \ \mathrm {[rad]} \ \)のときに最大又は最小となる。
三角波波高値は\( \ 1 \ \)で,上式の基本波の波高値を\( \ 1 \ \)とする信号波\( \ v_{\mathrm {u2}}^{*} \ \)としたときの変調率\( \ A_{\mathrm {2}} \ \)は,上記の変調率の定義式からいくつの数値となるかを示せ。
(5) (4)の\( \ \mathrm {PWM} \ \)制御方式\( \ 2 \ \)において,\( \ \mathrm {v} \ \)相,\( \ \mathrm {w} \ \)相出力電圧の信号波に\( \ v_{\mathrm {u2}}^{*} \ \)を基本波位相で\( \ \displaystyle \frac {2\pi }{3} \ \mathrm {[rad]} \ \),\( \ \displaystyle \frac {4\pi }{3} \ \mathrm {[rad]} \ \)ずつ遅らせた波形を用いる。このとき,(4)で求めた変調率\( \ A_{\mathrm {2}} \ \)を\( \ 1 \ \)とするように信号波を大きくすると,\( \ \mathrm {u}-\mathrm {v} \ \)相線間電圧\( \ v_{\mathrm {uv2}} \ \)の基本波実効値\( \ V_{\mathrm {uv2}} \ \)は,(3)で求めた\( \ V_{\mathrm {uvf1}} \ \)の何倍となるかを示せ。
【ワンポイント解説】
三相インバータから\( \ \mathrm {PWM} \ \)制御により出力を得る\( \ 1 \ \)種ではかなり出題されやすいパターンの問題であるかと思います。
十分に内容を理解していると\( \ 1 \ \)種のパワーエレクトロニクスとしては比較的取り組みやすい問題となりますが,制限時間のある電験受験生にはなかなか厳しい問題かもしれません。
1.\( \ \mathrm {PWM} \ \)制御と変調率
\( \ \mathrm {PWM} \ \)制御はパルス幅変調制御を意味し,出力の交流電圧をパルス幅で制御する方法となります。
出力電圧は交流電源の搬送波と信号波の大きさの比較により行います。
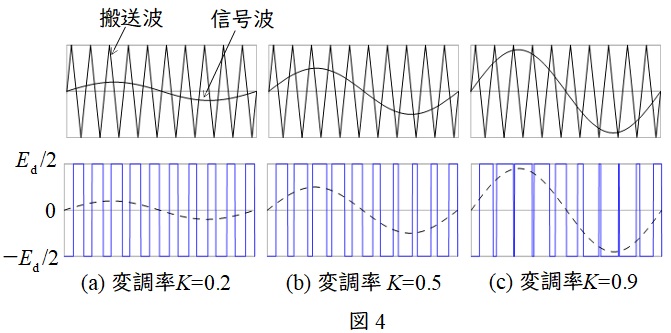
変調率は搬送波と信号波の振幅の比率をいい,図4のように搬送波と信号波の比率を変化させることで,変調率に比例した出力電圧を得ることができます。
【関連する「電気の神髄」記事】
【解答】
(1)信号波と三角波とを比較して,大小がどのような関係のときに上アーム\( \ \mathrm {IGBT} \ \)及び下アーム\( \ \mathrm {IGBT} \ \)をオン又はオフするか
(ポイント)
・図1において上アームがオン,下アームがオフのとき,三相負荷には\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \)が出力され,上アームがオフ,下アームがオンのとき,三相負荷には\( \ \displaystyle -\frac {E_{\mathrm {d}}}{2} \ \)が出力されます。
・図2において,三角波<信号波のとき\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \)が出力され,三角波>信号波のとき\( \ \displaystyle -\frac {E_{\mathrm {d}}}{2} \ \)が出力されています。
・上記\( \ 2 \ \)項目を理解した上で解答をすれば問題ありません。
(試験センター解答)
信号波が三角波よりも大きければ上アームの\( \ \mathrm {IGBT} \ \)をオンさせ,下アームの\( \ \mathrm {IGBT} \ \)をオフさせる。反対に,信号波が三角波よりも小さければ上アームの\( \ \mathrm {IGBT} \ \)をオフさせ,下アームの\( \ \mathrm {IGBT} \ \)をオンさせる。
(2)基本波電圧\( \ v_{\mathrm {uf1}} \ \),\( \ v_{\mathrm {vf1}} \ \),\( \ v_{\mathrm {wf1}} \ \)の瞬時値を,そのときの変調率\( \ A_{\mathrm {1}} \ \)及び\( \ E_{\mathrm {d}} \ \)を用いて,\( \ \sin \ \)を使った式で表す
ワンポイント解説「1.\( \ \mathrm {PWM} \ \)制御と変調率」の通り,変調率が\( \ 1 \ \)以下の場合において,出力の波形は信号波に変調率を乗じたものであることが分かる。
信号波の波高値は,「\( \ A_{\mathrm {1}}=1 \ \)の場合,基本波電圧\( \ v_{\mathrm {uf1}} \ \)の波高値は,インバータで出力できる最大電圧\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \)となる」となっていることから\( \ \displaystyle \frac {E_{\mathrm {d}}}{2} \ \)であるため,変調率\( \ A_{\mathrm {1}}=1 \ \)の場合の信号波\( \ v_{\mathrm {u1}}^{*1} \ \),\( \ v_{\mathrm {v1}}^{*1} \ \),\( \ v_{\mathrm {w1}}^{*1} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {u1}}^{*1} &=&\frac {E_{\mathrm {d}}}{2}\sin \omega t \\[ 5pt ]
v_{\mathrm {v1}}^{*1} &=&\frac {E_{\mathrm {d}}}{2}\sin \left( \omega t-\frac {2\pi }{3}\right) \\[ 5pt ]
v_{\mathrm {w1}}^{*1} &=&\frac {E_{\mathrm {d}}}{2}\sin \left( \omega t-\frac {4\pi }{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
となり,三つの基本波電圧\( \ v_{\mathrm {uf1}} \ \),\( \ v_{\mathrm {vf1}} \ \),\( \ v_{\mathrm {wf1}} \ \)は,これに変調率\( \ A_{\mathrm {1}} \ \)を乗じた,
\[
\begin{eqnarray}
v_{\mathrm {uf1}} &=&\frac {A_{\mathrm {1}}E_{\mathrm {d}}}{2}\sin \omega t \\[ 5pt ]
v_{\mathrm {vf1}} &=&\frac {A_{\mathrm {1}}E_{\mathrm {d}}}{2}\sin \left( \omega t-\frac {2\pi }{3}\right) \\[ 5pt ]
v_{\mathrm {wf1}} &=&\frac {A_{\mathrm {1}}E_{\mathrm {d}}}{2}\sin \left( \omega t-\frac {4\pi }{3}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)(2)で得た式の近似式を求める
\( \ A_{\mathrm {1}}=1 \ \)のときの出力波形\( \ v_{\mathrm {uf1}} \ \)の実効値\( \ V_{\mathrm {uf1}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {uf1}} &=&\frac {1}{\sqrt {2}}\cdot \frac {E_{\mathrm {d}}}{2} \\[ 5pt ]
&=&\frac {E_{\mathrm {d}}}{2\sqrt {2}} \\[ 5pt ]
\end{eqnarray}
\]
であり,線間電圧\( \ V_{\mathrm {uvf1}} \ \)は相電圧\( \ V_{\mathrm {uf1}} \ \)の\( \ \sqrt {3} \ \)倍の大きさであるから,
\[
\begin{eqnarray}
V_{\mathrm {uvf1}} &=&\sqrt {3}V_{\mathrm {uf1}} \\[ 5pt ]
&=&\sqrt {3}\cdot \frac {E_{\mathrm {d}}}{2\sqrt {2}} \\[ 5pt ]
&=&\frac {\sqrt {3}E_{\mathrm {d}}}{2\sqrt {2}} \\[ 5pt ]
&≒&0.61237E_{\mathrm {d}} → 0.612E_{\mathrm {d}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)基本波に波高値が\( \ \displaystyle \frac {1}{6} \ \)倍の\( \ 3 \ \)次高調波を加算した信号波の波高値
図3の通り,\( \ \displaystyle \omega t=\frac {\pi }{3} \ \mathrm {[rad]} \ \)のときが最大値となるから,与えられた信号波\( \ v_{\mathrm {u2}}^{*} \ \)にこれを代入すると,
\[
\begin{eqnarray}
v_{\mathrm {u2}}^{*} &=&\sin \omega t +\frac {1}{6}\sin 3\omega t \\[ 5pt ]
&=&\sin \omega \frac {\pi }{3} +\frac {1}{6}\sin \left( 3 \times \frac {\pi }{3} \right) \\[ 5pt ]
&=&\sin \omega \frac {\pi }{3} +\frac {1}{6}\sin \pi \\[ 5pt ]
&=&\frac {\sqrt {3}}{2}+0 \\[ 5pt ]
&=&\frac {\sqrt {3}}{2} \\[ 5pt ]
&≒&0.86603 → 0.866 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)(4)で求めた変調率\( \ A_{\mathrm {2}} \ \)を\( \ 1 \ \)とするように信号波を大きくすると,\( \ \mathrm {u}-\mathrm {v} \ \)相線間電圧\( \ V_{\mathrm {uv2}} \ \)は,(3)で求めた\( \ V_{\mathrm {uv1}} \ \)の何倍となるか
(4)より,\( \ A_{\mathrm {2}} \ \)を\( \ 1 \ \)とするための信号波\( \ v_{\mathrm {u2}}^{*1} \ \)は,
\[
\begin{eqnarray}
v_{\mathrm {u2}}^{*1} &=&\frac {2}{\sqrt {3}}\cdot \frac {E_{\mathrm {d}}}{2}v_{\mathrm {u2}}^{*} \\[ 5pt ]
&=&\frac {2}{\sqrt {3}}\cdot \frac {E_{\mathrm {d}}}{2}\sin \omega t +\frac {2}{\sqrt {3}}\cdot \frac {1}{6}\cdot \frac {E_{\mathrm {d}}}{2}\sin 3\omega t \\[ 5pt ]
&=&\frac {E_{\mathrm {d}}}{\sqrt {3}}\sin \omega t +\frac {1}{6\sqrt {3}}E_{\mathrm {d}}\sin 3\omega t \\[ 5pt ]
\end{eqnarray}
\]
となる。上式の基本波実効値\( \ V_{\mathrm {uf2}} \ \)は,
\[
\begin{eqnarray}
V_{\mathrm {uf2}} &=&\frac {1}{\sqrt {2}}\cdot \frac {E_{\mathrm {d}}}{\sqrt {3}} \\[ 5pt ]
&=&\frac {E_{\mathrm {d}}}{\sqrt {6}} \\[ 5pt ]
\end{eqnarray}
\]
であり,線間電圧\( \ V_{\mathrm {uvf2}} \ \)は相電圧\( \ V_{\mathrm {uf2}} \ \)の\( \ \sqrt {3} \ \)倍の大きさであるから,
\[
\begin{eqnarray}
V_{\mathrm {uvf2}} &=&\sqrt {3}V_{\mathrm {uf2}} \\[ 5pt ]
&=&\sqrt {3}\cdot \frac {E_{\mathrm {d}}}{\sqrt {6}} \\[ 5pt ]
&=&\frac {E_{\mathrm {d}}}{\sqrt {2}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。したがって,\( \ V_{\mathrm {uvf2}} \ \)と\( \ V_{\mathrm {uvf1}} \ \)の比は,
\[
\begin{eqnarray}
\frac {V_{\mathrm {uvf2}}}{V_{\mathrm {uvf1}}} &=&\frac {\displaystyle \frac {E_{\mathrm {d}}}{\sqrt {2}}}{\displaystyle \frac {\sqrt {3}E_{\mathrm {d}}}{2\sqrt {2}}} \\[ 5pt ]
&=&\frac {2}{\sqrt {3}} \\[ 5pt ]
&≒&1.1547 → 1.15 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん