【問題】
【難易度】★★☆☆☆(やや易しい)
同期リアクタンスが\( \ X_{\mathrm {s}}\left( =2 \ \mathrm {p.u.}\right) \ \)である小型の三相円筒形同期発電機を,その定格電圧(相電圧)\( \ V_{\mathrm {N}}\left( =1 \ \mathrm {p.u.}\right) \ \)と同じ電圧の母線に直接接続して運転したときの発電機の運転状態と界磁電流\( \ I_{\mathrm {f}} \ \mathrm {[p.u.]} \ \)の関係に関して,次の問に答えよ。
ただし,巻線抵抗及び各種損失は無視できるものとし,また鉄心の磁気飽和も無視して,発電機の無負荷誘導起電力\( \ E \ \mathrm {[p.u.]} \ \)は界磁電流\( \ I_{\mathrm {f}} \ \mathrm {[p.u.]} \ \)に比例して\( \ E=kI_{\mathrm {f}} \ \)で表されるものとする。なお,単位法は自己定格容量及び自己定格電圧を基準とする。
(1) 上記の条件で発電機を定格運転すると,皮相電力\( \ S_{\mathrm {N}}\left( =1 \ \mathrm {p.u.}\right) \ \),機械入力\( \ P_{\mathrm {N}}\left( =0.8 \ \mathrm {p.u.}\right) \ \),無効電力\( \ Q_{\mathrm {N}}\left( =0.6 \ \mathrm {p.u.}\right) \ \)(遅れ),界磁電流\( \ I_{\mathrm {fN}} \ \mathrm {[p.u.]} \ \),無負荷誘導起電力\( \ {\dot E}_{\mathrm {N}} \ \mathrm {[p.u.]} \ \),電機子電流\( \ {\dot I}_{\mathrm {N}} \left( I_{\mathrm {N}}=1 \ \mathrm {p.u.}\right) \ \),力率角は\( \ \theta _{\mathrm {N}} \ \)であった。
a.このときのフェーザ図を描き,図中に\( \ {\dot E}_{\mathrm {N}} \ \),\( \ {\dot V}_{\mathrm {N}} \ \),\( \ {\dot I}_{\mathrm {N}} \ \),\( \ \theta _{\mathrm {N}} \ \)及び\( \ \mathrm {j}X_{\mathrm {s}}{\dot I}_{\mathrm {N}} \ \)を記入せよ。また,\( \ E=kI_{\mathrm {f}} \ \)であることに留意して,図から\( \ I_{\mathrm {fN}} \ \)を\( \ V_{\mathrm {N}} \ \),\( \ I_{\mathrm {N}} \ \),\( \ \theta _{\mathrm {N}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ k \ \)で表す式を導出せよ。
b.求めた式に数値\( \ \left( \mathrm {p.u.}\right) \ \)を代入して,\( \ I_{\mathrm {fN}} \ \)を\( \ k \ \)のみで表す式を示せ。
(2) 定格運転の状態から,機械入力を一定に保ち無効電力を零とするように界磁電流を調整すると,界磁電流は\( \ I_{\mathrm {f2}} \ \mathrm {[p.u.]} \ \),電機子電流は\( \ {\dot I}_{\mathrm {2}} \ \mathrm {[p.u.]} \ \),無負荷誘導起電力は\( \ {\dot E}_{\mathrm {2}} \ \mathrm {[p.u.]} \ \)になった。
a.このときのフェーザ図を描き,図中に\( \ {\dot E}_{\mathrm {2}} \ \),\( \ {\dot V}_{\mathrm {N}} \ \),\( \ {\dot I}_{\mathrm {2}} \ \)及び\( \ \mathrm {j}X_{\mathrm {s}}{\dot I}_{\mathrm {2}} \ \)を記入せよ。また,図から\( \ I_{\mathrm {f2}} \ \)を\( \ I_{\mathrm {2}} \ \),\( \ V_{\mathrm {N}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ k \ \)で表す式を示せ。
b.求めた式に数値\( \ \left( \mathrm {p.u.}\right) \ \)を代入して,\( \ I_{\mathrm {f2}} \ \)を\( \ k \ \)のみで表す式を示せ。また,調整後の\( \ I_{\mathrm {f2}} \ \)は定格時の\( \ I_{\mathrm {fN}} \ \)の何%になるか答えよ。
(3) 定格運転の状態から,機械入力を零にして,かつ無効電力を\( \ Q_{\mathrm {N}} \ \)に維持するように界磁電流を調整すると,界磁電流は\( \ I_{\mathrm {f3}} \ \mathrm {[p.u.]} \ \),電機子電流は\( \ {\dot I}_{\mathrm {3}} \ \),無負荷誘導起電力は\( \ {\dot E}_{\mathrm {3}} \ \mathrm {[p.u.]} \ \)になった。
a.このときのフェーザ図を描き,図中に\( \ {\dot E}_{\mathrm {3}} \ \),\( \ {\dot V}_{\mathrm {N}} \ \),\( \ {\dot I}_{\mathrm {3}} \ \)及び\( \ \mathrm {j}X_{\mathrm {s}}{\dot I}_{\mathrm {3}} \ \)を記入せよ。また,図から\( \ I_{\mathrm {f3}} \ \)を\( \ I_{\mathrm {3}} \ \),\( \ V_{\mathrm {N}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ k \ \)で表す式を示せ。
b.求めた式に数値\( \ \left( \mathrm {p.u.}\right) \ \)を代入して,\( \ I_{\mathrm {f3}} \ \)を\( \ k \ \)のみで表す式を示せ。また,調整後の\( \ I_{\mathrm {f3}} \ \)は定格時の\( \ I_{\mathrm {fN}} \ \)の何%になるか答えよ。
【ワンポイント解説】
同期機の運転状態の変化に関する問題です。
少し分量は多めですが,難易度としてはかなり易しめの問題なので,選択する受験生も多かったのではないかと思います。同期機のベクトル図等は使いこなせるレベルになっておきましょう。
1.同期発電機の等価回路とベクトル図
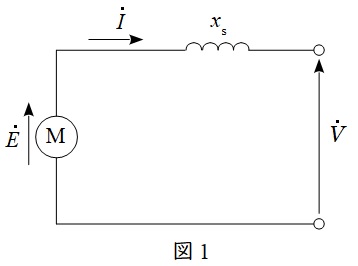
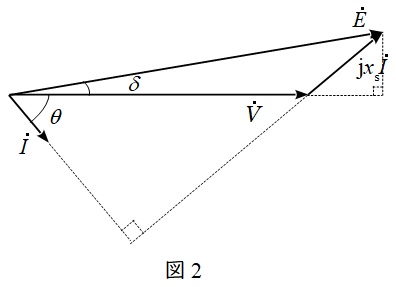
同期発電機の誘導起電力を\( \ \dot E \ \),端子電圧を\( \ \dot V \ \),同期リアクタンスを\( \ x_{\mathrm {s}} \ \),電機子電流を\( \ \dot I \ \)とすると,同期発電機の等価回路は図1,ベクトル図は図2のように描くことができます。
【解答】
(1)a.発電機を定格運転したときのフェーザ図を描き,\( \ I_{\mathrm {fN}} \ \)を\( \ V_{\mathrm {N}} \ \),\( \ I_{\mathrm {N}} \ \),\( \ \theta _{\mathrm {N}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ k \ \)で表す式を導出する
ワンポイント解説「1.同期発電機の等価回路とベクトル図」より,フェーザ図は図3のようになる。
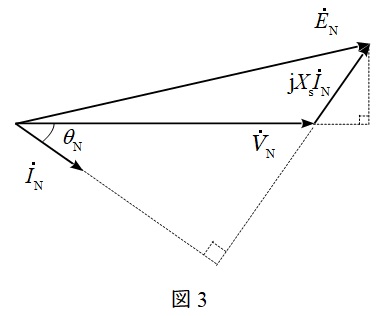
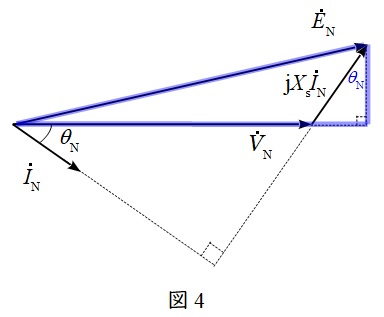
図3と同じフェーザ図である図4に示した三角形について三平方の定理を適用すると,
\[
\begin{eqnarray}
E_{\mathrm {N}}^{2}&=&\left( V_{\mathrm {N}}+X_{\mathrm {s}}I_{\mathrm {N}}\sin \theta _{\mathrm {N}}\right) ^{2}+\left( X_{\mathrm {s}}I_{\mathrm {N}}\cos \theta _{\mathrm {N}}\right) ^{2} \\[ 5pt ]
&=&V_{\mathrm {N}}^{2}+2V_{\mathrm {N}}X_{\mathrm {s}}I_{\mathrm {N}}\sin \theta _{\mathrm {N}}+X_{\mathrm {s}}^{2}I_{\mathrm {N}}^{2}\sin ^{2}\theta _{\mathrm {N}} + X_{\mathrm {s}}^{2}I_{\mathrm {N}}^{2}\cos ^{2}\theta _{\mathrm {N}} \\[ 5pt ]
&=&V_{\mathrm {N}}^{2}+2V_{\mathrm {N}}X_{\mathrm {s}}I_{\mathrm {N}}\sin \theta _{\mathrm {N}}+X_{\mathrm {s}}^{2}I_{\mathrm {N}}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ E_{\mathrm {N}}=kI_{\mathrm {fN}} \ \)であるから,
\[
\begin{eqnarray}
k^{2}I_{\mathrm {fN}}^{2}&=&V_{\mathrm {N}}^{2}+2V_{\mathrm {N}}X_{\mathrm {s}}I_{\mathrm {N}}\sin \theta _{\mathrm {N}}+X_{\mathrm {s}}^{2}I_{\mathrm {N}}^{2} \\[ 5pt ]
I_{\mathrm {fN}}^{2}&=&\frac {V_{\mathrm {N}}^{2}+2V_{\mathrm {N}}X_{\mathrm {s}}I_{\mathrm {N}}\sin \theta _{\mathrm {N}}+X_{\mathrm {s}}^{2}I_{\mathrm {N}}^{2}}{k^{2}} \\[ 5pt ]
I_{\mathrm {fN}}&=&\frac {\sqrt {V_{\mathrm {N}}^{2}+2V_{\mathrm {N}}X_{\mathrm {s}}I_{\mathrm {N}}\sin \theta _{\mathrm {N}}+X_{\mathrm {s}}^{2}I_{\mathrm {N}}^{2}}}{k} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(1)b.求めた式に数値\( \ \left( \mathrm {p.u.}\right) \ \)を代入して,\( \ I_{\mathrm {fN}} \ \)を\( \ k \ \)のみで表す式を示す
\( \ P_{\mathrm {N}}=V_{\mathrm {N}}I_{\mathrm {N}}\cos \theta _{\mathrm {N}} \ \)より,
\[
\begin{eqnarray}
\cos \theta _{\mathrm {N}}&=&\frac {P_{\mathrm {N}}}{V_{\mathrm {N}}I_{\mathrm {N}}} \\[ 5pt ]
&=&\frac {0.8}{1\times 1} \\[ 5pt ]
&=&0.8 \\[ 5pt ]
\sin \theta _{\mathrm {N}}&=&\sqrt {1-\cos ^{2}\theta _{\mathrm {N}}} \\[ 5pt ]
&=&\sqrt {1-0.8^{2}} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
であるから,(1)a.の解答式に各値を代入すると,
\[
\begin{eqnarray}
I_{\mathrm {fN}}&=&\frac {\sqrt {1^{2}+2\times 1\times 2\times 1 \times 0.6+2^{2}\times 1^{2}}}{k} \\[ 5pt ]
&=&\frac {\sqrt {7.4}}{k} \\[ 5pt ]
&≒&\frac {2.7203}{k} → \frac {2.72}{k} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)a.機械入力を一定に保ち無効電力を零とするように界磁電流を調整したときのフェーザ図を描き,\( \ I_{\mathrm {f2}} \ \)を\( \ I_{\mathrm {2}} \ \),\( \ V_{\mathrm {N}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ k \ \)で表す式を導出する
無効電力を零としたとき,\( \ V_{\mathrm {N}} \ \)と\( \ I_{\mathrm {2}} \ \)は同相となるから,フェーザ図は図5のようになる。

図5において三平方の定理を適用すると,
\[
\begin{eqnarray}
E_{\mathrm {2}}^{2}&=&V_{\mathrm {N}} ^{2}+\left( X_{\mathrm {s}}I_{\mathrm {2}}\right) ^{2} \\[ 5pt ]
&=&V_{\mathrm {N}}^{2}+X_{\mathrm {s}}^{2}I_{\mathrm {2}}^{2} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ E_{\mathrm {2}}=kI_{\mathrm {f2}} \ \)であるから,
\[
\begin{eqnarray}
k^{2}I_{\mathrm {f2}}^{2}&=&V_{\mathrm {N}}^{2}+X_{\mathrm {s}}^{2}I_{\mathrm {2}}^{2} \\[ 5pt ]
I_{\mathrm {f2}}^{2}&=&\frac {V_{\mathrm {N}}^{2}+X_{\mathrm {s}}^{2}I_{\mathrm {2}}^{2}}{k^{2}} \\[ 5pt ]
I_{\mathrm {f2}}&=&\frac {\sqrt {V_{\mathrm {N}}^{2}+X_{\mathrm {s}}^{2}I_{\mathrm {2}}^{2}}}{k} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)b.求めた式に数値\( \ \left( \mathrm {p.u.}\right) \ \)を代入して,\( \ I_{\mathrm {f2}} \ \)を\( \ k \ \)のみで表す式を示し,\( \ I_{\mathrm {fN}} \ \)の何%となるかを示す
\( \ P_{\mathrm {N}}=V_{\mathrm {N}}I_{\mathrm {2}} \ \)より,
\[
\begin{eqnarray}
I_{\mathrm {2}}&=&\frac {P_{\mathrm {N}}}{V_{\mathrm {N}}} \\[ 5pt ]
&=&\frac {0.8}{1} \\[ 5pt ]
&=&0.8 \\[ 5pt ]
\end{eqnarray}
\]
であるから,(2)a.の解答式に各値を代入すると,
\[
\begin{eqnarray}
I_{\mathrm {f2}}&=&\frac {\sqrt {1^{2}+2^{2}\times 0.8^{2}}}{k} \\[ 5pt ]
&=&\frac {\sqrt {3.56}}{k} \\[ 5pt ]
&≒&\frac {1.8868}{k} → \frac {1.89}{k} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ I_{\mathrm {fN}} \ \)と比較すると,
\[
\begin{eqnarray}
\frac {I_{\mathrm {f2}}}{I_{\mathrm {fN}}}&=&\frac {\displaystyle \frac {1.8868}{k}}{\displaystyle \frac {2.7203}{k}} \\[ 5pt ]
&≒&0.69360 → 69.4 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)a.機械入力を零にして,かつ無効電力を\( \ Q_{\mathrm {N}} \ \)に維持するように界磁電流を調整したときのフェーザ図を描き,\( \ I_{\mathrm {f3}} \ \)を\( \ I_{\mathrm {3}} \ \),\( \ V_{\mathrm {N}} \ \),\( \ X_{\mathrm {s}} \ \),\( \ k \ \)で表す式を導出する
機械入力を零としたとき,\( \ V_{\mathrm {N}} \ \)より\( \ I_{\mathrm {3}} \ \)は\( \ \displaystyle \frac {\pi }{2} \ \mathrm {[rad]} \ \)遅れとなるから,フェーザ図は図6のようになる。
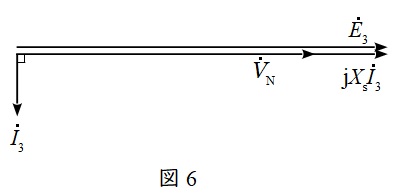
図6より,
\[
\begin{eqnarray}
E_{\mathrm {3}}&=&V_{\mathrm {N}} +X_{\mathrm {s}}I_{\mathrm {3}} \\[ 5pt ]
\end{eqnarray}
\]
であり,\( \ E_{\mathrm {3}}=kI_{\mathrm {f3}} \ \)であるから,
\[
\begin{eqnarray}
kI_{\mathrm {f3}}&=&V_{\mathrm {N}} +X_{\mathrm {s}}I_{\mathrm {3}} \\[ 5pt ]
I_{\mathrm {f3}}&=&\frac {V_{\mathrm {N}} +X_{\mathrm {s}}I_{\mathrm {3}}}{k} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)b.求めた式に数値\( \ \left( \mathrm {p.u.}\right) \ \)を代入して,\( \ I_{\mathrm {f3}} \ \)を\( \ k \ \)のみで表す式を示し,\( \ I_{\mathrm {fN}} \ \)の何%となるかを示す
\( \ Q_{\mathrm {N}}=V_{\mathrm {N}}I_{\mathrm {3}} \ \)より,
\[
\begin{eqnarray}
I_{\mathrm {3}}&=&\frac {Q_{\mathrm {N}}}{V_{\mathrm {N}}} \\[ 5pt ]
&=&\frac {0.6}{1} \\[ 5pt ]
&=&0.6 \\[ 5pt ]
\end{eqnarray}
\]
であるから,(3)a.の解答式に各値を代入すると,
\[
\begin{eqnarray}
I_{\mathrm {f3}}&=&\frac {1 +2\times 0.6}{k} \\[ 5pt ]
&=&\frac {2.2}{k} \ \mathrm {[p.u.]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,\( \ I_{\mathrm {fN}} \ \)と比較すると,
\[
\begin{eqnarray}
\frac {I_{\mathrm {f3}}}{I_{\mathrm {fN}}}&=&\frac {\displaystyle \frac {2.2}{k}}{\displaystyle \frac {2.7203}{k}} \\[ 5pt ]
&≒&0.80873 → 80.9 \ \mathrm {[%]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん