【問題】
【難易度】★★★☆☆（普通）
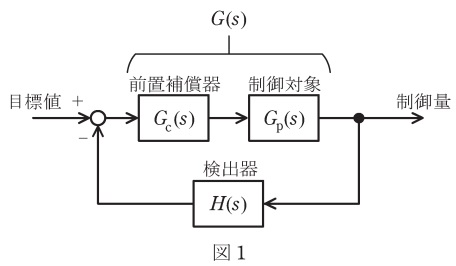
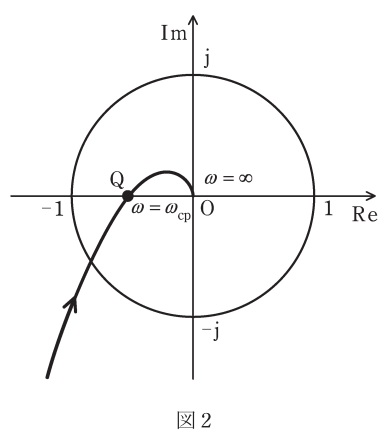
図1に示すフィードバック制御系において，角周波数\( \ \omega \ \mathrm {[rad/s]} \ \)を\( \ 0 \ \)から\( \ +\infty \ \)まで変化させたときの一巡周波数伝達関数\( \ G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \ \)のベクトル軌跡が図2であった。ゲイン余裕\( \ g_{\mathrm {m}} \ \)は，線分\( \ \mathrm {OQ} \ \)の長さを\( \ \overline {\mathrm {OQ}} \ \)で表すとき，\( \ \displaystyle g_{\mathrm {m}}=20\log _{10}\frac {1}{\overline {\mathrm {OQ}}} \ \mathrm {[dB]} \ \)で与えられる。位相交差角周波数を\( \ \omega _{\mathrm {cp}} \ \)とする。次の問に答えよ。
(1) \( \ \overline {\mathrm {OQ}} \ \)を一巡周波数伝達関数\( \ G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \ \)を用いて表せ。
(2) \( \ g_{\mathrm {m}}=20 \ \mathrm {dB} \ \)のとき\( \ \left| G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \right| \ \)が成立する条件式を対数関数を用いずに示せ。
(3) \( \ \displaystyle G_{\mathrm {p}}\left( s\right) =\frac {1}{\left( 1+3s\right) \left( 1+7s\right) } \ \)，\( \ G_{\mathrm {c}}\left( s\right) =K \ \)，\( \ \displaystyle H\left( s\right) =\frac {1}{1+s} \ \)であるとき，\( \ \omega _{\mathrm {cp}} \ \)の値を求めよ。ただし，\( \ K＞0 \ \)とする。
(4) 小問(3)のとき，ゲイン余裕を\( \ 20 \ \mathrm {dB} \ \)とする\( \ K \ \)の値を求めよ。
(5) 小問(3)のとき，制御系を安定限界とする\( \ K \ \)の値を求めよ。
(6) 小問(5)のときの閉ループ系の特性根\( \ \lambda \ \)を全て求めよ。
【ワンポイント解説】
電験\( \ 1 \ \)種としては近年出題の少ない古典制御からの問題ですが，\( \ 2 \ \)年連続して出題されているので，もしかすると傾向が変わってきているかもしれません。
全体として難易度は普通としていますが，(1)～(5)までは易しい問題で，(6)は高難度の問題となります。(6)の三次方程式の解き方は本解説を一例に覚えるようにして下さい。
ただし，合格基準を満たすためには(5)までを正解できれば十分なので，(6)は深追いせず参考程度に留めておいても良いかもしれません。
1.ナイキストの安定判別法
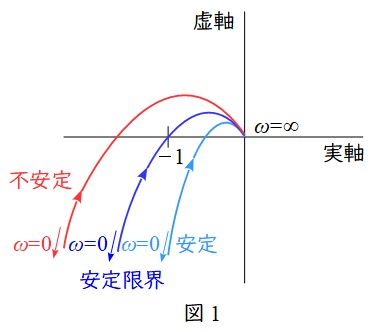
開ループ周波数伝達関数\( \ G_{0}( \mathrm {j}\omega ) \ \)が与えられている時，\( \ G_{0}( \mathrm {j}\omega ) \ \)が実軸と交わる点が，\( \ (-1，0 ) \ \)より右側ならば安定，左側ならば不安定，\( \ (-1，0 ) \ \)であれば安定限界となります。
2.ラウスの安定判別法
特性方程式\( \ a_{0}s^{n}+a_{1}s^{n-1}+a_{2}s^{n-2}+\cdots +a_{n-1}s+a_{n}=0 \ \)が与えられている時，ラウスの安定判別法による安定条件は，
\[
\begin{eqnarray}
&&1. s^{n}，s^{n-1}，\cdots ，s^{1}，s^{0}の係数がすべて存在 \\[ 5pt ]
&&2. s^{n}，s^{n-1}，\cdots ，s^{1}，s^{0}の係数がすべて同符号 \\[ 5pt ]
&&3. ラウスの数表の値がすべて正であること \\[ 5pt ]
\end{eqnarray}
\]
です。ラウスの数表は下図のようになります。
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
1行 & a_{0} & a_{2} & a_{4} & \cdots \\
2行 & a_{1} & a_{3} & a_{5} & \cdots \\
3行 & b_{1}=\frac {a_{1}a_{2}-a_{0}a_{3}}{a_{1}} & b_{2}=\frac {a_{1}a_{4}-a_{0}a_{5}}{a_{1}} & \cdots \\
4行 & c_{1}=\frac {b_{1}a_{3}-a_{1}b_{2}}{b_{1}} & c_{2}=\frac {b_{1}a_{5}-a_{1}b_{3}}{b_{1}} & \cdots \\
\vdots & \vdots & \vdots &
\end{array}
\]
【解答】
(1)\( \ \overline {\mathrm {OQ}} \ \)を一巡周波数伝達関数\( \ G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \ \)を用いて表す
\( \ Q \ \)の状態にあるのは，\( \ \omega =\omega _{\mathrm {cp}} \ \)の時であるから，\( \ \overline {\mathrm {OQ}} \ \)は，
\[
\begin{eqnarray}
\overline {\mathrm {OQ}} &=& \left| G\left( \mathrm {j}\omega _{\mathrm {cp}} \right) H\left( \mathrm {j}\omega _{\mathrm {cp}} \right) \right| \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)\( \ g_{\mathrm {m}}=20 \ \mathrm {dB} \ \)のとき\( \ \left| G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \right| \ \)が成立する条件式
\( \ \displaystyle g_{\mathrm {m}}=20\log _{10}\frac {1}{\overline {\mathrm {OQ}}} \ \mathrm {[dB]} \ \)なので，
\[
\begin{eqnarray}
g_{\mathrm {m}} &=& 20\log _{10}\frac {1}{\overline {\mathrm {OQ}}} \\[ 5pt ]
&=& 20\log _{10}\frac {1}{\left| G\left( \mathrm {j}\omega _{\mathrm {cp}} \right) H\left( \mathrm {j}\omega _{\mathrm {cp}} \right) \right| } \\[ 5pt ]
&=& -20\log _{10}\left| G\left( \mathrm {j}\omega _{\mathrm {cp}} \right) H\left( \mathrm {j}\omega _{\mathrm {cp}} \right) \right| \\[ 5pt ]
\end{eqnarray}
\]
となる。上式に各値を代入すると，
\[
\begin{eqnarray}
20 &=& -20\log _{10}\left| G\left( \mathrm {j}\omega _{\mathrm {cp}} \right) H\left( \mathrm {j}\omega _{\mathrm {cp}} \right) \right| \\[ 5pt ]
-1 &=& \log _{10}\left| G\left( \mathrm {j}\omega _{\mathrm {cp}} \right) H\left( \mathrm {j}\omega _{\mathrm {cp}} \right) \right| \\[ 5pt ]
\left| G\left( \mathrm {j}\omega _{\mathrm {cp}} \right) H\left( \mathrm {j}\omega _{\mathrm {cp}} \right) \right| &=& 10^{-1} \\[ 5pt ]
&=& 0.1 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ \displaystyle G_{\mathrm {p}}\left( s\right) =\frac {1}{\left( 1+3s\right) \left( 1+7s\right) } \ \)，\( \ G_{\mathrm {c}}\left( s\right) =K \ \)，\( \ \displaystyle H\left( s\right) =\frac {1}{1+s} \ \)であるとき，\( \ \omega _{\mathrm {cp}} \ \)の値
一巡周波数伝達関数\( \ G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \ \)に各値を代入すると，
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) &=& G_{\mathrm {p}}\left( \mathrm {j}\omega \right) G_{\mathrm {c}}\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \\[ 5pt ]
&=& \frac {1}{\left( 1+\mathrm {j}3\omega \right) \left( 1+\mathrm {j}7\omega \right) }\cdot K \cdot \frac {1}{1+\mathrm {j}\omega} \\[ 5pt ]
&=& \frac {K}{\left( 1+\mathrm {j}3\omega \right) \left( 1+\mathrm {j}7\omega \right) \left( 1+\mathrm {j}\omega \right) } \\[ 5pt ]
&=& \frac {K}{\left( 1-21\omega ^{2}+\mathrm {j}10\omega \right) \left( 1+\mathrm {j}\omega \right) } \\[ 5pt ]
&=& \frac {K}{1+\mathrm {j}\omega -21\omega ^{2}-\mathrm {j}21\omega ^{3}+\mathrm {j}10\omega -10\omega ^{2} } \\[ 5pt ]
&=& \frac {K}{1-31\omega ^{2}+\mathrm {j}\omega \left( 11 -21\omega ^{2}\right) } \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ \omega =\omega _{\mathrm {cp}} \ \)の時，上式の虚数部は零となるから，
\[
\begin{eqnarray}
11 -21\omega _{\mathrm {cp}} ^{2} &=& 0 \\[ 5pt ]
\omega _{\mathrm {cp}} ^{2}&=& \frac {11}{21} \\[ 5pt ]
\omega _{\mathrm {cp}}&=& \sqrt {\frac {11}{21}} \ \left( ∵\omega _{\mathrm {cp}}＞0\right) \\[ 5pt ]
&≒& 0.72375 → 0.724 \ \mathrm {[rad/s]} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)小問(3)のとき，ゲイン余裕を\( \ 20 \ \mathrm {dB} \ \)とする\( \ K \ \)の値
(3)より，
\[
\begin{eqnarray}
G\left( \mathrm {j}\omega _{\mathrm {cp}}\right) H\left( \mathrm {j}\omega _{\mathrm {cp}}\right) &=& \frac {K}{1-31\omega _{\mathrm {cp}}^{2}} \\[ 5pt ]
&=& \frac {K}{\displaystyle 1-31\times \frac {11}{21}} \\[ 5pt ]
&=& -\frac {K}{15.238} \\[ 5pt ]
\end{eqnarray}
\]
であり，(2)より，\( \ g_{\mathrm {m}}=20 \ \mathrm {dB} \ \)のとき\( \ \left| G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \right| =0.1 \ \)であるから，これを上式に代入して\( \ K \ \)を求めると，
\[
\begin{eqnarray}
0.1 &=& \frac {K}{15.238} \\[ 5pt ]
K &=& 0.1\times 15.238 \\[ 5pt ]
&=& 1.5238 → 1.52 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)小問(3)のとき，制御系を安定限界とする\( \ K \ \)の値
制御系を安定限界とするためには，\( \ \left| G\left( \mathrm {j}\omega \right) H\left( \mathrm {j}\omega \right) \right| =1 \ \)とすれば良いので，
\[
\begin{eqnarray}
1 &=& \frac {K}{15.238} \\[ 5pt ]
K &=& 15.238 → 15.2 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(6)小問(5)のときの閉ループ系の特性根\( \ \lambda \ \)を全て
図1より，閉ループ系の伝達関数\( \ W \left( s \right) \ \)は，
\[
\begin{eqnarray}
W \left( s \right) &=& \frac {G\left( s \right) }{1+G\left( s \right) H\left( s \right) } \\[ 5pt ]
\end{eqnarray}
\]
であるから，特性方程式は，
\[
\begin{eqnarray}
1+G\left( s \right) H\left( s \right) &=& 0 \\[ 5pt ]
1+G_{\mathrm {p}}\left( s\right) G_{\mathrm {c}}\left( s\right) H\left( s \right) &=& 0 \\[ 5pt ]
1+\frac {1}{\left( 1+3s\right) \left( 1+7s\right) }\cdot K\cdot \frac {1}{1+s} &=& 0 \\[ 5pt ]
1+\frac {K}{\left( 1+3s\right) \left( 1+7s\right) \left( 1+s\right) } &=& 0 \\[ 5pt ]
1+\frac {K}{\left( 21s^{2}+10s+1\right) \left( 1+s\right) } &=& 0 \\[ 5pt ]
1+\frac {K}{ 21s^{3}+31s^{2}+11s+1 } &=& 0 \\[ 5pt ]
21s^{3}+31s^{2}+11s+\left( K+1\right) &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで，ワンポイント解説「2.ラウスの安定判別法」の通り，ラウスの数表を書くと，
\[
\begin{array}{c|ccc}
& 1列 & 2列 & 3列 \\
\hline
s^{3} & 21 & 11 & 0 \\
s^{2} & 31 & K+1 & 0 \\
s^{1} & \frac {320-21K}{31} & 0 \\
s^{0} & K+1 & 0 \\
\end{array}
\]
となる。ここで，安定限界であるとき，\( \ \displaystyle K=\displaystyle 31\times \frac {11}{21}-1≒15.238 \ \)となり，ラウスの数表の\( \ s^{1} \ \)の行が全て零になることがわかる。
このとき，虚軸上に特性根があり，\( \ s^{2} \ \)の行について以下の方程式，
\[
\begin{eqnarray}
31s^{2} +\left( K+1 \right) &=& 0 \\[ 5pt ]
31s^{2} +16.238 &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
が成立する。上式と解くと，
\[
\begin{eqnarray}
s^{2} &=& -\frac {16.238}{31} \\[ 5pt ]
s &=& \sqrt {-\frac {16.238}{31}} \\[ 5pt ]
&=& ±\mathrm {j}0.72374 \\[ 5pt ]
\end{eqnarray}
\]
となり，これらが特性方程式の根となる。もう一つの根を\( \ \lambda _{0} \ \)とすると，
\[
\begin{eqnarray}
\left( s-\lambda _{0} \right) \left( s+\mathrm {j}0.72374 \right) \left( s-\mathrm {j}0.72374 \right)&=& 0 \\[ 5pt ]
\left( s-\lambda _{0} \right) \left( s^{2}+0.52380 \right) &=& 0 \\[ 5pt ]
s^{3}-\lambda _{0} s^{2}+0.52380s-0.52380\lambda _{0} &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
となり，これが特性方程式
\[
\begin{eqnarray}
21s^{3}+31s^{2}+11s+16.238&=& 0 \\[ 5pt ]
s^{3}+1.4762s^{2}+0.52380s+0.77324 &=& 0 \\[ 5pt ]
\end{eqnarray}
\]
と一致しなければならないので，もう一つの根は\( \ \lambda _{0} =-1.4762 \ \)と求められる。
以上から，３つの特性根\( \ \lambda \ \)は，\( \ -1.48，±\mathrm {j}0.724 \ \)と求められる。
愛知県出身 愛称たけちゃん