【問題】
【難易度】★★☆☆☆(やや易しい)
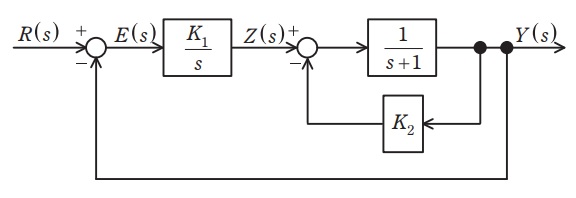
図に示すフィードバック制御系について,次の問に答えよ。ただし,\( \ R\left( s\right) \ \)は目標値,\( \ Y\left( s\right) \ \)は制御量,\( \ E\left( s\right) \ \)は制御偏差,\( \ Z\left( s\right) \ \)は積分器の出力であり,時間信号\( \ r\left( t\right) \ \),\( \ y\left( t\right) \ \),\( \ e\left( t\right) \ \),\( \ z\left( t\right) \ \)をそれぞれラプラス変換したものである。また,\( \ K_{1} \ \),\( \ K_{2} \ \)は定数である。
(1) 目標値\( \ R\left( s\right) \ \)から制御量\( \ Y\left( s\right) \ \)までの伝達関数\( \ T_{\mathrm {YR}}\left( s\right) \ \)を求めよ。
(2) \( \ T_{\mathrm {YR}}\left( s\right) \ \)を二次遅れ要素の標準形で表したときの減衰係数を\( \ \zeta =0.5 \ \),固有角周波数を\( \ \omega _{\mathrm {n}} = 10 \ \mathrm {rad / s} \ \)とするための\( \ K_{1} \ \),\( \ K_{2} \ \)の値を求めよ。
(3) 目標値\( \ R\left( s\right) \ \)から制御偏差\( \ E\left( s\right) \ \)までの伝達関数\( \ T_{\mathrm {ER}}\left( s\right) \ \)を求めよ。このとき,小問(2)の\( \ K_{1} \ \),\( \ K_{2} \ \)を用いよ。
(4) 小問(3)の結果を用いて,目標値\( \ R\left( s\right) \ \)を単位ランプ変化させたときの定常速度偏差\( \ e_{\mathrm {v}} \ \)をラプラス変換の最終値の定理を適用して求めよ。
(5) 小問(3)の結果を用いて,目標値\( \ R\left( s\right) \ \)を単位ランプ変化させたときの制御偏差の時間応答\( \ e\left( t\right) \ \)を計算せよ。その上で,\( \ e\left( \infty\right) \ \)を求め,小問(4)で求めた\( \ e_{\mathrm {v}} \ \)と一致することを確かめよ。
【ワンポイント解説】
フィードバック制御系に関する問題です。
伝達関数を導出して,二次遅れ標準形と比較したり,最終値の定理を使用する等\( \ 1 \ \)種の自動制御の問題としては珍しいオーソドックスな問題でした。
ぜひ本問は完答を目指すようにしましょう。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\hline
\end{array}
\]
2.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)
二次遅れの伝達関数\( \ W(s) \ \)の一般式は,減衰係数\( \ \zeta \ \),固有角周波数\( \ \omega _{\mathrm {n}} \ \)とすると,
\[
\begin{eqnarray}
W(s)&=&\frac {\omega _{\mathrm {n}}^{2}}{s^{2}+2\zeta \omega _{\mathrm {n}}s+\omega _{\mathrm {n}}^{2}} \\[ 5pt ]
\end{eqnarray}
\]
で表されます。
3.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
(1)目標値\( \ R\left( s\right) \ \)から制御量\( \ Y\left( s\right) \ \)までの伝達関数\( \ T_{\mathrm {YR}}\left( s\right) \ \)
問題図における\( \ R\left( s\right) \ \),\( \ Y\left( s\right) \ \),\( \ E\left( s\right) \ \),\( \ Z\left( s\right) \ \)の関係式は,
\[
\begin{eqnarray}
R\left( s\right) -Y\left( s\right) &=&E\left( s\right) &・・・・・・・・・ ①& \\[ 5pt ]
\frac {K_{1}}{s}E\left( s\right) &=&Z\left( s\right) &・・・・・・・・・ ②& \\[ 5pt ]
\left\{ Z\left( s\right) -K_{2}Y\left( s\right) \right\}\frac {1}{s+1} &=&Y\left( s\right) &・・・・・・・・・ ③& \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ ① \ \)を\( \ ② \ \)に代入すると,
\[
\begin{eqnarray}
\frac {K_{1}}{s}\left\{ R\left( s\right) -Y\left( s\right) \right\} &=&Z\left( s\right) &・・・・・・・・・ ②^{\prime }& \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ ②^{\prime } \ \)を\( \ ③ \ \)に代入して整理すると,
\[
\begin{eqnarray}
\left[ \frac {K_{1}}{s}\left\{ R\left( s\right) -Y\left( s\right) \right\} -K_{2}Y\left( s\right) \right] \frac {1}{s+1} &=&Y\left( s\right) \\[ 5pt ]
\frac {K_{1}}{s}\left\{ R\left( s\right) -Y\left( s\right) \right\} -K_{2}Y\left( s\right) &=&\left( s+1\right) Y\left( s\right) \\[ 5pt ]
K_{1}\left\{ R\left( s\right) -Y\left( s\right) \right\} -K_{2}sY\left( s\right) &=&s\left( s+1\right) Y\left( s\right) \\[ 5pt ]
K_{1}R\left( s\right) &=&s^{2} Y\left( s\right) +sY\left( s\right) +K_{1}Y\left( s\right) +K_{2}sY\left( s\right) \\[ 5pt ]
K_{1}R\left( s\right) &=&\left\{ s^{2} +\left( K_{2}+1\right) s+K_{1}\right\} Y\left( s\right) \\[ 5pt ]
\frac {Y\left( s\right)}{R\left( s\right) } &=&\frac {K_{1}}{s^{2} +\left( K_{2}+1\right) s+K_{1}} \\[ 5pt ]
T_{\mathrm {YR}}\left( s\right) &=&\frac {K_{1}}{s^{2} +\left( K_{2}+1\right) s+K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)減衰係数を\( \ \zeta =0.5 \ \),固有角周波数を\( \ \omega _{\mathrm {n}} = 10 \ \mathrm {rad / s} \ \)とするための\( \ K_{1} \ \),\( \ K_{2} \ \)の値
(1)解答式を二次遅れ標準形と比較すると,ワンポイント解説「2.減衰係数\( \ \zeta \ \)と固有角周波数\( \ \omega _{\mathrm {n}} \ \)」の通り,
\[
\begin{eqnarray}
2\zeta \omega _{\mathrm {n}}=K_{2}+1&=&10 \\[ 5pt ]
K_{2}&=&9 \\[ 5pt ]
\omega _{\mathrm {n}}^{2}=K_{1}&=&100 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)目標値\( \ R\left( s\right) \ \)から制御偏差\( \ E\left( s\right) \ \)までの伝達関数\( \ T_{\mathrm {ER}}\left( s\right) \ \)
(1)解答式より,
\[
\begin{eqnarray}
Y\left( s\right) &=&\frac {K_{1}}{s^{2} +\left( K_{2}+1\right) s+K_{1}}R\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
であるから,これを\( \ ① \ \)に代入して整理すると,
\[
\begin{eqnarray}
R\left( s\right) -\frac {K_{1}}{s^{2} +\left( K_{2}+1\right) s+K_{1}}R\left( s\right) &=&E\left( s\right) \\[ 5pt ]
\frac {s^{2} +\left( K_{2}+1\right) s}{s^{2} +\left( K_{2}+1\right) s+K_{1}}R\left( s\right) &=&E\left( s\right) \\[ 5pt ]
\frac {E\left( s\right) }{R\left( s\right) } &=&\frac {s^{2} +\left( K_{2}+1\right) s}{s^{2} +\left( K_{2}+1\right) s+K_{1}} \\[ 5pt ]
T_{\mathrm {ER}}\left( s\right) &=&\frac {s^{2} +\left( K_{2}+1\right) s}{s^{2} +\left( K_{2}+1\right) s+K_{1}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,これに\( \ K_{1}=100 \ \),\( \ K_{2}=9 \ \)を代入すれば,
\[
\begin{eqnarray}
T_{\mathrm {ER}}\left( s\right) &=&\frac {s^{2} +\left( 9+1\right) s}{s^{2} +\left( 9+1\right) s+100} \\[ 5pt ]
&=&\frac {s^{2} +10 s}{s^{2} +10s+100} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)目標値\( \ R\left( s\right) \ \)を単位ランプ変化させたときの定常速度偏差\( \ e_{\mathrm {v}} \ \)
(3)解答式より,
\[
\begin{eqnarray}
E\left( s\right) &=&\frac {s^{2} +10 s}{s^{2} +10s+100}R\left( s\right) \\[ 5pt ]
\end{eqnarray}
\]
であり,ワンポイント解説「1.基本的なラプラス変換」の通り,ランプ関数のラプラス変換は\( \ \displaystyle \frac {1}{s^{2}} \ \)であるから,
\[
\begin{eqnarray}
E\left( s\right) &=&\frac {s^{2} +10 s}{s^{2} +10s+100}\cdot \frac {1}{s^{2}} \\[ 5pt ]
&=&\frac {s +10 }{s^{3} +10s^{2}+100s} &・・・・・・・・・・・・ ④&\\[ 5pt ]
\end{eqnarray}
\]
となる。これに最終値の定理を適用させ定常速度偏差\( \ e_{\mathrm {v}} \ \)を求めると,ワンポイント解説「3.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } e\left( t\right) &=&\displaystyle \lim _{ s \to 0 } sE\left( s\right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left( s\cdot \frac {s +10 }{s^{3} +10s^{2}+100s}\right) \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \left( \frac {s +10 }{s^{2} +10s+100}\right) \\[ 5pt ]
&=&0.1 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)目標値\( \ R\left( s\right) \ \)を単位ランプ変化させたときの制御偏差の時間応答\( \ e\left( t\right) \ \)及び\( \ e\left( \infty\right) \ \)
\( \ ④ \ \)について,部分分数分解をするため,
\[
\begin{eqnarray}
\frac {s +10 }{s^{3} +10s^{2}+100s}&=&\frac {A}{s}+\frac {Bs+c}{s^{2} +10s+100} \\[ 5pt ]
\end{eqnarray}
\]
とおき,右辺を計算していくと,
\[
\begin{eqnarray}
\frac {A}{s}+\frac {Bs+C}{s^{2} +10s+100}&=&\frac {A\left( s^{2} +10s+100\right) +s\left( Bs+C\right) }{s^{3} +10s^{2}+100s} \\[ 5pt ]
&=&\frac {\left( A+B\right) s^{2} +\left( 10A+C\right) s+100A }{s^{3} +10s^{2}+100s} \\[ 5pt ]
\end{eqnarray}
\]
となるので,係数比較すれば,
\[
\begin{eqnarray}
A+B &=&0 \\[ 5pt ]
10A+C &=&1 \\[ 5pt ]
100A &=&10& \\[ 5pt ]
\end{eqnarray}
\]
であるから,\( \ A=0.1 \ \),\( \ B=-0.1 \ \),\( \ C=0 \ \)となる。よって,
\[
\begin{eqnarray}
E\left( s\right) &=&\frac {0.1}{s}-\frac {0.1s}{s^{2} +10s+100} \\[ 5pt ]
&=&\frac {0.1}{s}-\frac {0.1s}{\left( s+5\right) ^{2}+75} \\[ 5pt ]
&=&\frac {0.1}{s}-\frac {0.1\left( s+5\right) -0.5}{\left( s+5\right) ^{2}+75} \\[ 5pt ]
&=&\frac {0.1}{s}-\frac {0.1\left( s+5\right) }{\left( s+5\right) ^{2}+75}+ \frac {0.5}{\left( s+5\right) ^{2}+75} \\[ 5pt ]
&=&\frac {0.1}{s}-\frac {0.1\left( s+5\right) }{\left( s+5\right) ^{2}+\left( 5\sqrt {3}\right) ^{2}}+\frac {0.1}{\sqrt {3}}\cdot \frac {5\sqrt {3}}{\left( s+5\right) ^{2}+\left( 5\sqrt {3}\right) ^{2}} \\[ 5pt ]
&=&0.1\left\{ \frac {1}{s}-\frac {s+5}{\left( s+5\right) ^{2}+\left( 5\sqrt {3}\right) ^{2}}+\frac {1}{\sqrt {3}}\cdot \frac {5\sqrt {3}}{\left( s+5\right) ^{2}+\left( 5\sqrt {3}\right) ^{2}}\right\} \\[ 5pt ]
\end{eqnarray}
\]
となるから,逆ラプラス変換すると,ワンポイント解説「1.基本的なラプラス変換」の通り,
\[
\begin{eqnarray}
e\left( t\right) &=&0.1\left( 1-\mathrm {e}^{-5t}\cos 5\sqrt {3}t+\frac {1}{\sqrt {3}}\mathrm {e}^{-5t}\sin 5\sqrt {3}t\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,上式より\( \ e\left( \infty\right) \ \)は,
\[
\begin{eqnarray}
e\left( \infty \right) &=&\displaystyle \lim _{ t \to \infty } \left\{ 0.1\left( 1-\mathrm {e}^{-5t}\cos 5\sqrt {3}t+\frac {1}{\sqrt {3}}\mathrm {e}^{-5t}\sin 5\sqrt {3}t\right) \right\} \\[ 5pt ]
&=& 0.1\times \left( 1-0+0\right) \\[ 5pt ]
&=& 0.1 \\[ 5pt ]
\end{eqnarray}
\]
となり,(4)で求めた\( \ e_{\mathrm {v}} \ \)と一致する。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん