【問題】
【難易度】★★☆☆☆(やや易しい)
図1のブロック線図は制御対象,図2のブロック線図はフィードフォワード・フィードバック制御器を表している。
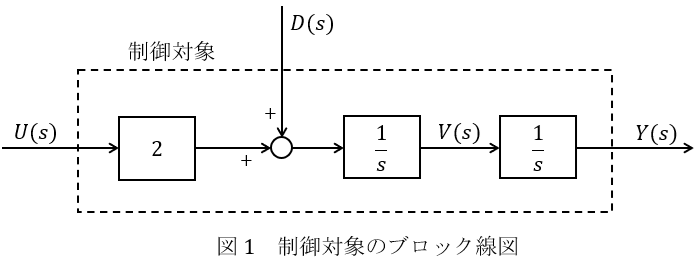
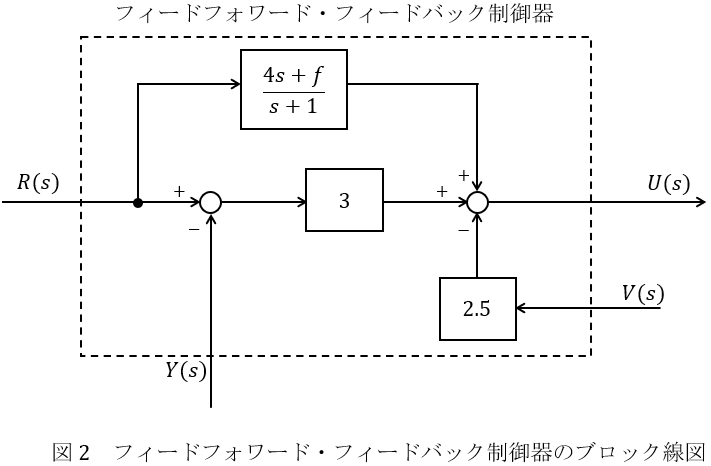
なお,\( \ R(s) \ \)は目標信号,\( \ Y(s) \ \)は制御量,\( \ V(s) \ \)は制御量の変化率(微分)を表す量,\( \ U(s) \ \)は操作量,\( \ D(s) \ \)は外乱である。図1の\( \ \displaystyle \frac {1}{s} \ \)は積分器,\( \ \displaystyle \frac {4s+f}{s+1} \ \)の\( \ f \ \)は実数パラメータである。このとき,以下の問に答えよ。ただし,伝達関数で答える場合は,分母多項式,分子多項式は\( \ s \ \)の降べきの順で表し,分母多項式の最高次係数は\( \ 1 \ \)とする。また,伝達関数の分母多項式と分子多項式に共通因子があればそれらは消去する。
(1) 図1のブロック線図が表す信号間の関係から\( \ Y(s) \ \)を\( \ U(s) \ \),\( \ D(s) \ \)を用いて表せ。 また,\( \ V(s) \ \)を\( \ Y(s) \ \)を用いて表せ。
(2) (1)で求めた\( \ V(s) \ \)と\( \ Y(s) \ \)の関係および図2のブロック線図が表す信号間の関係を用いて\( \ U(s) \ \)を\( \ R(s) \ \),\( \ Y(s) \ \)を用いて表せ。
(3) (1),(2)を用いて\( \ R(s) \ \)から\( \ Y(s) \ \)への閉ループ伝達関数\( \ T_{1}(s) \ \)および\( \ D(s) \ \)から\( \ Y(s) \ \)への閉ループ伝達関数\( \ T_{2}(s) \ \)を求めよ。
(4) 伝達関数\( \ T_{2}(s) \ \)に対して角周波数\( \ 1 \ \mathrm {rad / s} \ \)の正弦波信号が加わったときのゲインを求めよ。ただし,\( \ \sqrt {2}=1.41 \ \)とする。
(5) \( \ R(s) \ \)および\( \ D(s) \ \)は単位ステップ信号,すなわち\( \ \mathcal {L}^{-1}\left[ R(s)\right] =\mathcal {L}^{-1}\left[ D(s)\right] =1 \ \)とする。このとき,制御量\( \ Y(s) \ \)の逆ラプラス変換\( \ y(t) =\mathcal {L}^{-1}\left[ Y(s)\right] \ \)の定常値が\( \ 1 \ \),すなわち\( \ y(\infty ) =1 \ \)となるように\( \ f \ \)の値を定めよ。
【ワンポイント解説】
フィードフォワード・フィードバック制御の伝達関数に関する問題です。
計算量は多めですが,電験\( \ 1 \ \)種の問題としてはかなりオーソドックスな問題と言えます。
計算間違いに注意して\( \ 30 \ \)分以内の完答を目指すようにしましょう。
1.基本的なラプラス変換
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると以下のような関係があります。
\[
\begin{array}{|c|c|}
\hline
f(t) & F(s) \\
\hline
{\displaystyle \delta (t) }\atop{単位インパルス関数} & 1 \\[ 5pt ]
{\displaystyle u (t) }\atop{単位ステップ関数} & \displaystyle \frac {1}{s} \\[ 5pt ]
K & \displaystyle \frac {K}{s} \\[ 5pt ]
t & \displaystyle \frac {1}{s^{2}} \\[ 5pt ]
\mathrm {e}^{at} & \displaystyle \frac {1}{s-a} \\[ 5pt ]
\sin \omega t & \displaystyle \frac {\omega }{s^{2}+\omega ^{2}} \\[ 5pt ]
\cos \omega t & \displaystyle \frac {s}{s^{2}+\omega ^{2}} \\[ 5pt ]
\displaystyle \frac {\mathrm {d}f\left( t \right) }{\mathrm {d}t} & sF\left( s \right) -f\left( 0 \right) \\[ 5pt ]
\displaystyle \int f\left( t \right) \mathrm {d}t & \displaystyle \frac {F\left( s \right) }{s}+\frac {1}{s}\int _{-\infty }^{0}f\left( \tau \right) \mathrm {d}\tau \\[ 5pt ]
\hline
\end{array}
\]
2.ブロック線図の考え方
①直列
図1のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
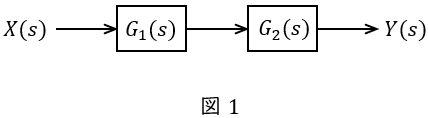
②並列
図2のような伝達関数\( \ G_{1}(s) \ \),\( \ G_{2}(s) \ \)が与えられているとき,全体の伝達関数\( \ G(s) \ \)は,
\[
\begin{eqnarray}
G(s)&=&\frac {Y(s)}{X(s)}=G_{1}(s)±G_{2}(s) \\[ 5pt ]
\end{eqnarray}
\]
となります。
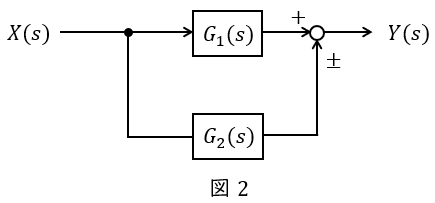
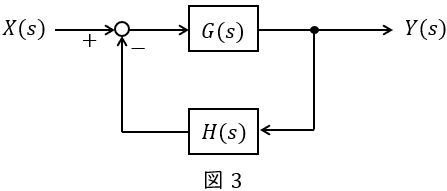
③フィードバック
図3のような\( \ G(s) \ \),\( \ H(s) \ \)が与えられているとき,全体の伝達関数\( \ W(s) \ \)は,
\[
\begin{eqnarray}
Y(s)&=&\left\{ X(s) -H(s)Y(s) \right\} G(s) \\[ 5pt ]
Y(s)&=&G(s)X(s) -G(s)H(s)Y(s) \\[ 5pt ]
Y(s)+G(s)H(s)Y(s) &=&G(s)X(s) \\[ 5pt ]
\left\{ 1+G(s)H(s)\right\} Y(s) &=&G(s)X(s) \\[ 5pt ]
\frac {Y(s)}{X(s)}&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
W(s)&=&\frac {G(s)}{1+G(s)H(s)} \\[ 5pt ]
\end{eqnarray}
\]
となります。
3.最終値の定理
\( \ f(t) \ \)のラプラス変換を\( \ F(s) \ \)とすると,\( \ f(t) \ \)の定常値は,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } f(t)&=&\displaystyle \lim _{ s \to 0 } sF(s) \\[ 5pt ]
\end{eqnarray}
\]
で求められます。
【解答】
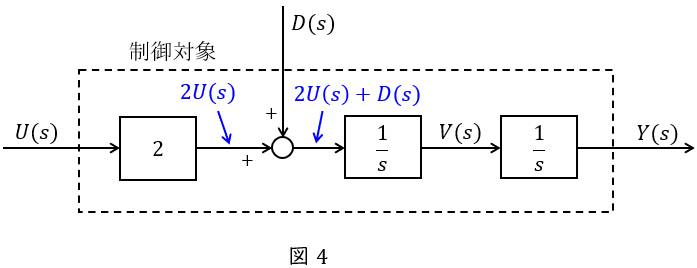
(1)\( \ Y(s) \ \)を\( \ U(s) \ \),\( \ D(s) \ \)を用いて表す, \( \ V(s) \ \)を\( \ Y(s) \ \)を用いて表す
図4に示すようにブロック線図上の信号\( \ 2U(s) \ \),\( \ 2U(s)+D(s) \ \)が求められるので,
\[
\begin{eqnarray}
Y(s)&=&\frac {1}{s}\cdot \frac {1}{s}\cdot \left\{ 2U(s)+D(s) \right\} \\[ 5pt ]
&=&\frac {2}{s^{2}}U(s)+\frac {1}{s^{2}}D(s) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。また,
\[
\begin{eqnarray}
Y(s)&=&\frac {1}{s}V(s) \\[ 5pt ]
V(s)&=&sY(s) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
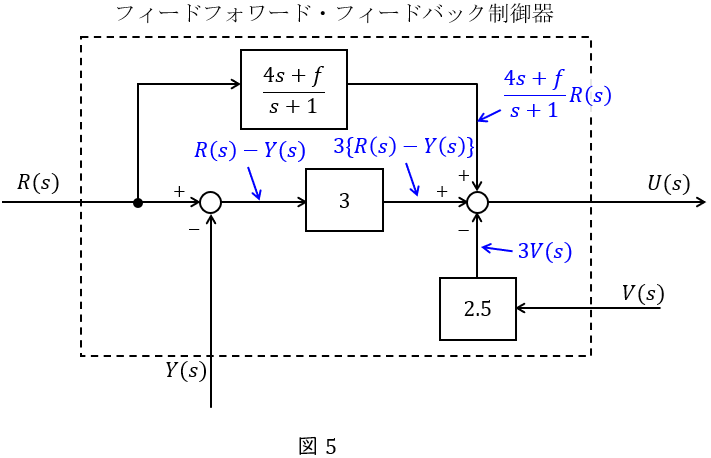
(2)\( \ U(s) \ \)を\( \ R(s) \ \),\( \ Y(s) \ \)を用いて表す
ブロック線図上の\( \ U(s) \ \)に入る各信号は図5のようになるので\( \ U(s) \ \)は,
\[
\begin{eqnarray}
U(s)&=&\frac {4s+f}{s+1}R(s)+3\left\{ R(s)-Y(s)\right\}-2.5V(s) \\[ 5pt ]
\end{eqnarray}
\]
となり,(1)より\( \ V(s)=sY(s) \ \)であるから,
\[
\begin{eqnarray}
U(s)&=&\frac {4s+f}{s+1}R(s)+3\left\{ R(s)-Y(s)\right\}-2.5sY(s) \\[ 5pt ]
&=&\left( \frac {4s+f}{s+1}+3\right) R(s)-\left( 2.5s+3\right) Y(s) \\[ 5pt ]
&=&\left\{ \frac {4s+f+3\left( s+1\right) }{s+1}\right\} R(s)-\left( 2.5s+3\right) Y(s) \\[ 5pt ]
&=&\left( \frac {7s+f+3 }{s+1}\right) R(s)-\left( 2.5s+3\right) Y(s) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)\( \ R(s) \ \)から\( \ Y(s) \ \)への閉ループ伝達関数\( \ T_{1}(s) \ \)および\( \ D(s) \ \)から\( \ Y(s) \ \)への閉ループ伝達関数\( \ T_{2}(s) \ \)
(2)解答式を(1)解答式に代入すると,
\[
\begin{eqnarray}
Y(s)&=&\frac {2}{s^{2}}U(s)+\frac {1}{s^{2}}D(s) \\[ 5pt ]
&=&\frac {2}{s^{2}}\left\{ \left( \frac {7s+f+3 }{s+1}\right) R(s)-\left( 2.5s+3\right) Y(s)\right\} +\frac {1}{s^{2}}D(s) \\[ 5pt ]
&=&\frac {14s+2f+6 }{s^{2}\left( s+1\right) } R(s)- \frac {5s+6}{s^{2}} Y(s) +\frac {1}{s^{2}}D(s) \\[ 5pt ]
Y(s)+\frac {5s+6}{s^{2}} Y(s) &=&\frac {14s+2f+6 }{s^{2}\left( s+1\right) } R(s) +\frac {1}{s^{2}}D(s) \\[ 5pt ]
\frac {s^{2}+5s+6}{s^{2}} Y(s) &=&\frac {14s+2f+6 }{s^{2}\left( s+1\right) } R(s) +\frac {1}{s^{2}}D(s) \\[ 5pt ]
\left( s^{2}+5s+6\right) Y(s) &=&\frac {14s+2f+6 }{ s+1 } R(s) +D(s) \\[ 5pt ]
Y(s) &=&\frac {14s+2f+6 }{ \left( s+1\right) \left( s^{2}+5s+6\right) } R(s) +\frac {1}{s^{2}+5s+6}D(s) \\[ 5pt ]
&=&\frac {14s+2f+6 }{ s^{3}+6s^{2}+11s+6 } R(s) +\frac {1}{s^{2}+5s+6}D(s) \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ R(s) \ \)から\( \ Y(s) \ \)への閉ループ伝達関数\( \ T_{1}(s) \ \)および\( \ D(s) \ \)から\( \ Y(s) \ \)への閉ループ伝達関数\( \ T_{2}(s) \ \)は,
\[
\begin{eqnarray}
T_{1}(s) &=&\frac {14s+2f+6 }{ s^{3}+6s^{2}+11s+6 } \\[ 5pt ]
T_{2}(s) &=&\frac {1}{s^{2}+5s+6} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)伝達関数\( \ T_{2}(s) \ \)に対して角周波数\( \ 1 \ \mathrm {rad / s} \ \)の正弦波信号が加わったときのゲイン
\( \ T_{2}(s) \ \)の周波数伝達関数\( \ T_{2}(\mathrm {j}\omega ) \ \)は,
\[
\begin{eqnarray}
T_{2}(\mathrm {j}\omega ) &=&\frac {1}{\left( \mathrm {j}\omega \right) ^{2}+\mathrm {j}5\omega +6} \\[ 5pt ]
&=&\frac {1}{\left( 6-\omega ^{2} \right) +\mathrm {j}5\omega } \\[ 5pt ]
\end{eqnarray}
\]
となり,ゲインは,
\[
\begin{eqnarray}
\left| T_{2}(\mathrm {j}\omega ) \right| &=&\frac {1}{\sqrt {\left( 6-\omega ^{2} \right) ^{2}+25\omega ^{2}}} \\[ 5pt ]
\end{eqnarray}
\]
となる。よって,\( \ \omega =1 \ \mathrm {[rad / s]} \ \)の正弦波信号が加わったときのゲインは,
\[
\begin{eqnarray}
\left| T_{2}(\mathrm {j}1 ) \right| &=&\frac {1}{\sqrt {\left( 6-1 ^{2} \right) ^{2}+25\times 1 ^{2}}} \\[ 5pt ]
&≒&0.141 \ 42 → 0.141 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)\( \ y(\infty ) =1 \ \)となるような\( \ f \ \)の値
単位ステップ信号のラプラス変換は,ワンポイント解説「1.基本的なラプラス変換」の通り\( \ \displaystyle \frac {1}{s} \ \)なので,(3)の\( \ Y(s) \ \)の式に代入して整理すると,
\[
\begin{eqnarray}
Y(s) &=&\frac {14s+2f+6 }{ s^{3}+6s^{2}+11s+6 } R(s) +\frac {1}{s^{2}+5s+6}D(s) \\[ 5pt ]
&=&\frac {14s+2f+6 }{ s^{3}+6s^{2}+11s+6 } \cdot \frac {1}{s} +\frac {1}{s^{2}+5s+6}\cdot \frac {1}{s} \\[ 5pt ]
&=&\frac {14s+2f+6 }{ s^{3}+6s^{2}+11s+6 } \cdot \frac {1}{s} +\frac {s+1}{\left( s+1\right) \left( s^{2}+5s+6\right)}\cdot \frac {1}{s} \\[ 5pt ]
&=&\frac {14s+2f+6 +s+1}{ s^{3}+6s^{2}+11s+6 } \cdot \frac {1}{s} \\[ 5pt ]
&=&\frac {15s+2f+7}{ s^{3}+6s^{2}+11s+6 } \cdot \frac {1}{s} \\[ 5pt ]
\end{eqnarray}
\]
となり,これに最終値の定理を適用すると,ワンポイント解説「3.最終値の定理」の通り,
\[
\begin{eqnarray}
\displaystyle \lim _{ t \to \infty } y(t)&=&\displaystyle \lim _{ s \to 0 } sY(s) \\[ 5pt ]
1&=&\displaystyle \lim _{ s \to 0 } s\cdot \frac {15s+2f+7}{ s^{3}+6s^{2}+11s+6 } \cdot \frac {1}{s} \\[ 5pt ]
&=&\displaystyle \lim _{ s \to 0 } \frac {15s+2f+7}{ s^{3}+6s^{2}+11s+6 } \\[ 5pt ]
&=&\frac {2f+7}{6 } \\[ 5pt ]
2f+7&=&6 \\[ 5pt ]
2f&=&-1 \\[ 5pt ]
f&=&-0.5 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん