【問題】
【難易度】★★☆☆☆(やや易しい)
次の文章は,平等磁界中に置かれた鉄心の磁化の強さに関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる式又は数値を解答群の中から選び,その記号をマークシートに記入しなさい。
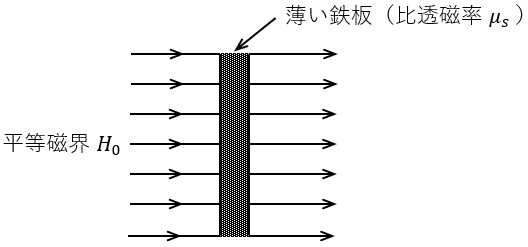
真空中において,図のように無限に広く薄い鉄板が平等磁界\( \ H_{0} \ \)に垂直に置いてある。真空の透磁率を\( \ \mu _{0} \ \),鉄板の比透磁率を\( \ \mu _{s} \ \)とするとき,鉄板内の磁束密度,磁界,磁化の強さ及び減磁率の大きさを求めてみよう。
一般に磁性体があるときの磁界分布では磁束密度を\( \ \boldsymbol {B} \ \)(ベクトル)とするとき,発散記号を\( \ \mathrm {div} \ \)とすれば磁束密度\( \ \boldsymbol {B} \ \)は連続であるから\( \ \fbox { (1) } \ \)である。
したがって,鉄板内の磁束密度\( \ B_{i} \ \)は\( \ \fbox { (2) } \ \)である。また,鉄板内の磁界\( \ H_{i} \ \)は磁束密度と同じ方向で\( \ \fbox { (3) } \ \)となる。さらに,磁化の強さ\( \ M \ \)は,磁束密度及び磁界と同方向で\( \ \fbox { (4) } \ \)となる。鉄板内の磁界の強さ\( \ H_{i} \ \)は外部の磁界の強さ\( \ H_{0} \ \)に対して減磁力\( \ H_{d}=H_{0}-H_{i} \ \)だけ小さくなっている。減磁力は磁化の強さに比例し,その比例定数である減磁率はこの場合\( \ \fbox { (5) } \ \)となり,最も大きい値となる。
〔問1の解答群〕
\[
\begin{eqnarray}
&(イ)& \mathrm {div} \boldsymbol {B}=\mu _{0}H_{0} &(ロ)& \frac {1}{\mu _{s}}H_{0} &(ハ)& \left( 1+\frac {1}{\mu _{s}}\right) \mu _{0}H_{0} \\[ 5pt ]
&(ニ)& 0.5 &(ホ)& \mu _{0}\mu _{s}H_{0} &(ヘ)& \left( 1-\frac {1}{\mu _{s}}\right) H_{0} \\[ 5pt ]
&(ト)& \left( 1+\mu _{s}\right) \mu _{0}H_{0} &(チ)& \mathrm {div} \boldsymbol {B}=0 &(リ)& 1.5 \\[ 5pt ]
&(ヌ)& \left( 1-\frac {1}{\mu _{s}}\right) \mu _{0}H_{0} &(ル)& H_{0} &(ヲ)& 1.0 \\[ 5pt ]
&(ワ)& \left( 1+\frac {1}{\mu _{s}}\right) H_{0} &(カ)& \mu _{0}H_{0} &(ヨ)& \mathrm {div} \boldsymbol {B}=\mu _{0}\mu _{s}H_{0} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
平等磁界中に置かれた鉄心内の磁界及び磁化に関する問題です。
発散の\( \ \mathrm {div} \ \)の内容が出てくる等少しだけ応用的な内容を含みますが,計算量はそれほど多くないため,高得点を目指したい問題です。
\( \ 2 \ \)種まででは磁化の内容はあまり出てきませんが,電磁気のテキストには磁化率の内容も含め記載がありますので,理解しておくようにしましょう。
1.\( \ \mathrm {div} \ \)(発散)
数学における\( \ \mathrm {div} \ \)(発散)は,
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E&=&\frac { \partial E_{\mathrm {x}}}{ \partial x }+\frac { \partial E_{\mathrm {y}}}{ \partial y } +\frac { \partial E_{\mathrm {z}}}{ \partial z } \\[ 5pt ]
\end{eqnarray}
\]
で定義され,内積を用いて表すと,
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol E &=& \nabla \cdot \boldsymbol E \\[ 5pt ]
\end{eqnarray}
\]
となります。\( \ \nabla \ \)は数学で\( \ \displaystyle \nabla =\frac { \partial }{ \partial x }\boldsymbol i+\frac { \partial }{ \partial y }\boldsymbol j+\frac { \partial }{ \partial z }\boldsymbol k \ \)で定義される演算子です。
2.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係
図1に示すように透磁率が\( \ \mu \ \mathrm {[H / m]} \ \)の磁性体がある時,磁性体内の磁束密度\( \ B \ \mathrm {[T]} \ \)と磁界の大きさ\( \ H \ \mathrm {[A / m]} \ \)の関係は,真空の透磁率を\( \ \mu _{0} \ \mathrm {[H / m]} \ \),真空中での磁界の大きさを\( \ H_{0} \ \mathrm {[A / m]} \ \)とすると,真空中も磁性体内も磁束密度が変わらないことから,
\[
\begin{eqnarray}
B&=&\mu H=\mu _{0}H_{0} \\[ 5pt ]
\end{eqnarray}
\]
となります。また,磁性体の真空に対する比透磁率を\( \ \mu _{\mathrm {s}} \ \)とすると,
\[
\begin{eqnarray}
B&=&\mu _{\mathrm {s}}\mu _{0} H \\[ 5pt ]
\end{eqnarray}
\]
となります。このときの磁性体の磁化の強さを\( \ M \ \mathrm {[A / m]} \ \)とすれば,
\[
\begin{eqnarray}
B&=&\mu _{0} \left( H+M\right) \\[ 5pt ]
\end{eqnarray}
\]
という関係も成立します。

【解答】
(1)解答:チ
ワンポイント解説「1.\( \ \mathrm {div} \ \)(発散)」の通り,磁性体内の磁束密度\( \ \boldsymbol {B} \ \)が連続であるとき,どの方向にも変化はないので,
\[
\begin{eqnarray}
\mathrm {div} \boldsymbol B&=&\frac { \partial B_{\mathrm {x}}}{ \partial x }+\frac { \partial B_{\mathrm {y}}}{ \partial y } +\frac { \partial B_{\mathrm {z}}}{ \partial z } \\[ 5pt ]
&=&0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:カ
鉄板内の磁束密度\( \ B_{i} \ \)は,真空中の磁束密度と等しいので,ワンポイント解説「2.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係」の通り,
\[
\begin{eqnarray}
B_{i}&=&\mu _{0}H_{0} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ロ
鉄板内の磁界\( \ H_{i} \ \)は,磁束密度が等しいことから,ワンポイント解説「2.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係」の通り,
\[
\begin{eqnarray}
B_{i}=\mu _{\mathrm {s}}\mu _{0}H_{i} &=&\mu _{0}H_{0} \\[ 5pt ]
\mu _{\mathrm {s}}H_{i} &=&H_{0} \\[ 5pt ]
H_{i} &=&\frac {1}{\mu _{s}}H_{0} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:ヘ
磁束密度を求める式から磁化の強さ\( \ M \ \)は,ワンポイント解説「2.磁束密度\( \ B \ \)と磁界の大きさ\( \ H \ \)の関係」の通り,
\[
\begin{eqnarray}
B_{i}=\mu _{0}H_{0}&=&\mu _{0} \left( H_{i}+M\right) \\[ 5pt ]
H_{0}&=& H_{i}+M \\[ 5pt ]
M&=&H_{0}-H_{i} \\[ 5pt ]
&=&H_{0}-\frac {1}{\mu _{s}}H_{0} \\[ 5pt ]
&=&\left( 1-\frac {1}{\mu _{s}}\right) H_{0} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ヲ
題意より,減磁率\( \ \beta _{M} \ \)は,
\[
\begin{eqnarray}
\beta _{M}&=&\frac {H_{d}}{M} \\[ 5pt ]
&=&\frac {H_{0}-H_{i}}{H_{0}-H_{i}} \\[ 5pt ]
&=&1.0 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん