【問題】
【難易度】★★★☆☆(普通)
次の文章は,演算増幅器を用いたウィーンブリッジ発振回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまる語句,式又は数値を解答群の中から選び,その記号を記述用紙の解答欄に記入しなさい。
図1に示すウィーンブリッジ発振回路の発振条件を求めるために演算増幅器の非反転入力端子で切り離し,非反転入力端子に電圧源\( \ v_{1} \ \)を接続する。図2は,このようにして得られた回路であり,演算増幅器と抵抗\( \ R_{a} \ \)と\( \ R_{b} \ \)からなる回路と二つの抵抗\( \ R \ \)と二つの静電容量\( \ C \ \)からなる回路が縦続接続されて構成されている。ただし,以下では\( \ v_{1} \ \)の角周波数を\( \ \omega \ \)とする。
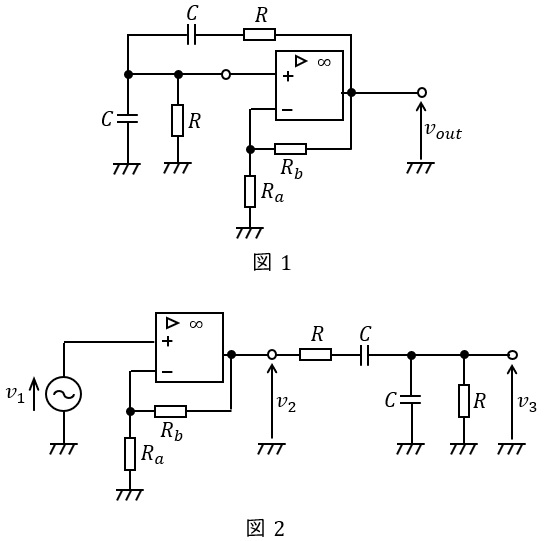
まず,演算増幅器と抵抗\( \ R_{a} \ \)と\( \ R_{b} \ \)からなる回路は\( \ \fbox { (1) } \ \)と呼ばれ,
\[
\begin{eqnarray}
\frac {v_{2}}{v_{1}} &=& \ \fbox { (2) } \ ・・・・・・・・・・・・ ① \\[ 5pt ]
\end{eqnarray}
\]
となる。また,
\[
\begin{eqnarray}
\frac {v_{3}}{v_{2}} &=& \ \fbox { (3) } \ ・・・・・・・・・・・・ ② \\[ 5pt ]
\end{eqnarray}
\]
となる。回路が発振するための一つの条件として\( \ v_{2} \ \)と\( \ v_{3} \ \)の位相差が零とならなければならない。②式から\( \ v_{2} \ \)と\( \ v_{3} \ \)の位相差は\( \ \omega = \ \fbox { (4) } \ \)のとき零となる。さらに,この条件の下で\( \ \displaystyle \frac {v_{3}}{v_{1}} =1 \ \)であれば回路は発振する。したがって,\( \ R_{a} \ \)が\( \ 3 \ \mathrm {[k\Omega ]} \ \)のとき\( \ R_{b} \ \)を\( \ \fbox { (5) } \ \mathrm {[k\Omega ]} \ \)とすれば図1のウィーンブリッジ発振回路は発振する。
〔問7の解答群〕
\[
\begin{eqnarray}
&(イ)& \frac {R_{b}}{R_{a}}+1 &(ロ)& 積分回路 &(ハ)& 6 \\[ 5pt ]
&(ニ)& \frac {\sqrt {3}}{CR} &(ホ)& 4 &(ヘ)& \frac {j\omega CR}{1+\omega ^{2}C^{2}R^{2}+j3\omega CR} \\[ 5pt ]
&(ト)& 逆相増幅回路 &(チ)& \frac {1}{CR} &(リ)& \frac {R_{b}}{R_{a}}-1 \\[ 5pt ]
&(ヌ)& \frac {j\omega CR}{1-\omega ^{2}C^{2}R^{2}+j2\omega CR} &(ル)& 正相増幅回路 &(ヲ)& \frac {R_{a}}{R_{b}}+1 \\[ 5pt ]
&(ワ)& \frac {\sqrt {2}}{CR} &(カ)& 1 &(ヨ)& \frac {j\omega CR}{1-\omega ^{2}C^{2}R^{2}+j3\omega CR} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
演算増幅器を用いたウィーンブリッジ発振回路に関する問題です。
計算量が少し多いですが,演算増幅器の特性を理解していればあとは回路計算のみの内容となります。
配点も高いため,合格のためには高得点を狙いたい問題と言えるでしょう。
1.理想的な演算増幅器の特徴
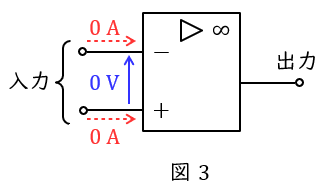
電験で出題される理想的な演算増幅器は以下のような特徴があります。
1.電圧増幅率が無限大である。したがって,無限大でない有限数が出力される時,入力端子間の電圧は\( \ 0 \ \mathrm {V} \ \)(バーチャルショート)となる。
2.入力インピーダンスが無限大である。したがって入力端子に電流は流れない。
3.出力インピーダンスがゼロである。
【解答】
(1)解答:ル
題意より解答候補は,(ロ)積分回路,(ト)逆相増幅回路,(ル)正相増幅回路,になると思います。
実際に(2)の計算をすれば分かりますが,図2のような回路では,\( \ v_{1} \ \)と\( \ v_{2} \ \)の位相は反転しないので,正相増幅回路(非反転増幅回路)といいます。
(2)解答:イ
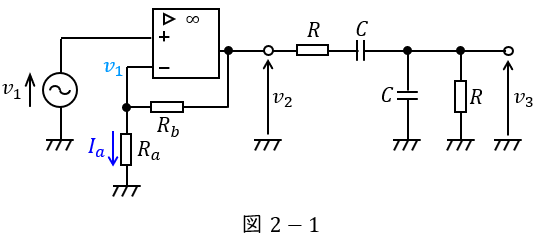
図2-1に示すように演算増幅器の-端子の電圧は,ワンポイント解説「1.理想的な演算増幅器の特徴」の通り,\( \ v_{1} \ \)となるから,\( \ R_{a} \ \)を流れる電流\( \ I_{a} \ \)は,
\[
\begin{eqnarray}
I_{a} &=& \frac {v_{1}}{R_{a}}\\[ 5pt ]
\end{eqnarray}
\]
となり,ワンポイント解説「1.理想的な演算増幅器の特徴」の通り,演算増幅器に電流は流れないので,\( \ R_{b} \ \)を流れる電流も\( \ I_{a} \ \)となる。したがって,\( \ v_{2} \ \)は,
\[
\begin{eqnarray}
v_{2} &=& v_{1}+R_{b}I_{a} \\[ 5pt ]
&=& v_{1}+R_{b}\cdot \frac {v_{1}}{R_{a}} \\[ 5pt ]
&=& \left( \frac {R_{b}}{R_{a}}+1\right) v_{1} \\[ 5pt ]
\end{eqnarray}
\]
となるから,\( \ \displaystyle \frac {v_{2}}{v_{1}} \ \)は,
\[
\begin{eqnarray}
\frac {v_{2}}{v_{1}} &=& \frac {R_{b}}{R_{a}}+1 \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(3)解答:ヨ
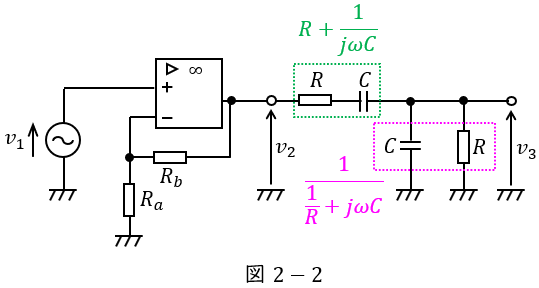
図2-2に示す通り,\( \ R \ \)と\( \ C \ \)の直列合成インピーダンスは\( \ \displaystyle R+\frac {1}{j\omega C} \ \),\( \ R \ \)と\( \ C \ \)の並列合成インピーダンスは\( \ \displaystyle \frac {1}{\displaystyle \frac {1}{R}+j\omega C} \ \)であるから,分圧の法則より,
\[
\begin{eqnarray}
v_{3} &=& \frac {\displaystyle \frac {1}{\displaystyle \frac {1}{R}+j\omega C}}{\displaystyle R+\frac {1}{j\omega C}+\displaystyle \frac {1}{\displaystyle \frac {1}{R}+j\omega C}}v_{2} \\[ 5pt ]
&=& \frac {1}{\displaystyle \left( R+\frac {1}{j\omega C}\right) \left( \frac {1}{R}+j\omega C\right) +1} v_{2} \\[ 5pt ]
&=& \frac {1}{\displaystyle \left( 1+j\omega CR+\frac {1}{j\omega CR}+1\right) +1} v_{2} \\[ 5pt ]
&=& \frac {1}{\displaystyle 3+j\omega CR+\frac {1}{j\omega CR}} v_{2} \\[ 5pt ]
&=& \frac {j\omega CR}{j3\omega CR-\omega ^{2}C^{2}R^{2}+1} v_{2} \\[ 5pt ]
&=& \frac {j\omega CR}{1-\omega ^{2}C^{2}R^{2}+j3\omega CR} v_{2} \\[ 5pt ]
\frac {v_{3}}{v_{2}}&=& \frac {j\omega CR}{1-\omega ^{2}C^{2}R^{2}+j3\omega CR} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:チ
(3)解答式において位相差が零,すなわち実数となるのは,分母の実部が零のときであるから,
\[
\begin{eqnarray}
1-\omega ^{2}C^{2}R^{2} &=& 0 \\[ 5pt ]
\omega ^{2}C^{2}R^{2} &=& 1 \\[ 5pt ]
\omega ^{2} &=& \frac {1}{C^{2}R^{2}} \\[ 5pt ]
\omega &=& \frac {1}{CR} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ハ
(4)の条件が成立するとき,\( \ \displaystyle \frac {v_{3}}{v_{2}} \ \)は,
\[
\begin{eqnarray}
\frac {v_{3}}{v_{2}}&=& \frac {j\omega CR}{j3\omega CR} \\[ 5pt ]
&=& \frac {1}{3} \\[ 5pt ]
\end{eqnarray}
\]
であり,これと(2)解答式より,回路が発信するのは,
\[
\begin{eqnarray}
\frac {v_{3}}{v_{1}} &=& 1 \\[ 5pt ]
\frac {v_{3}}{v_{2}}\cdot \frac {v_{2}}{v_{1}}&=&1 \\[ 5pt ]
\frac {1}{3}\cdot \left( \frac {R_{b}}{R_{a}}+1\right) &=& 1 \\[ 5pt ]
\frac {R_{b}}{R_{a}}+1&=& 3 \\[ 5pt ]
\frac {R_{b}}{R_{a}}&=&2 \\[ 5pt ]
\end{eqnarray}
\]
となるので,\( \ R_{a}=3 \ \mathrm {[k\Omega ]} \ \)のとき\( \ R_{b} =6 \ \mathrm {[k\Omega ]} \ \)と求められる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん