《理論》〈電子理論〉[H24:問4]nチャネルのMOSトランジスタに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★☆☆（普通）

次の文章は，$ \ \mathrm {n} \ $チャネルの$ \ \mathrm {MOS} \ $トランジスタに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も近いものを解答群の中から選びなさい。なお，$ \ \mathrm {SiO_{2}} \ $の誘電率$ \ 3.4\times 10^{-13} \ \mathrm {[F\cdot {cm}^{-1}]} \ $，単位電荷$ \ 1.6\times 10^{-19} \ \mathrm {[C]} \ $，シリコンでの電子移動度$ \ 1.0\times 10^{3} \ \mathrm {[{cm}^{2}\cdot {V}^{-1}\cdot {s}^{-1}]} \ $を計算に用いること。

$ \ \mathrm {MOS} \ $トランジスタでは，ゲート電圧$ \ V_{\mathrm {G}} \ $をしきい値電圧$ \ V_{\mathrm {T}} \ $より大きくするとチャネルが反転状態になる。ゲート電圧としきい値電圧間の電位差$ \ \left( V_{\mathrm {G}}-V_{\mathrm {T}}\right) \ $をオーバードライブ電圧と呼ぶ。電子の熱分布を無視すれば，$ \ \mathrm {MOS} \ $構造を$ \ \mathrm {SiO_{2}} \ $を絶縁物とした平行平板コンデンサとして考えることができる。このとき，反転状態にある単位面積当たりの電子の面電荷密度は，面積当たりの容量とオーバードライブ電圧との積になる。$ \ \mathrm {SiO_{2}} \ $の膜厚が$ \ 1.0\times 10^{-6} \ \mathrm {[cm]} \ $であるとした場合，反転層にある電子の面電荷密度を$ \ -5.0\times 10^{-7} \ \mathrm {[C\cdot {cm}^{-2}]} \ $とするために必要なオーバードライブ電圧は$ \ \fbox {　（１）　} \ \mathrm {[V]} \ $である。この面電荷密度は電子のキャリア濃度にすると$ \ \fbox {　（２）　} \ \mathrm {[{cm}^{-2}]} \ $である。

いまドレーン－ソース間の電圧が小さいときチャネル内の電子がドレーンへ向かうための電界の大きさは一様と考えてよいとする。チャネルの長さが$ \ 5.0\times 10^{-4} \ \mathrm {[cm]} \ $，ドレーン－ソース間電圧が$ \ 0.10 \ \mathrm {[V]} \ $であるとすれば，チャネル内の電子がドレーンへ向かうための電界の大きさは$ \ \fbox {　（３）　} \ \mathrm {[V\cdot {cm}^{-1}]} \ $である。ここで，電子の速度は，電子移動度と電界の積となることから，電子の速度は$ \ \fbox {　（４）　} \ \mathrm {[cm\cdot {s}^{-1}]} \ $となる。

電流密度は，流れる電荷密度と速度の積で表されることから，オーバードライブ電圧が$ \ \fbox {　（１）　} \ \mathrm {[V]} \ $で，ドレーン－ソース間電圧が$ \ 0.10 \ \mathrm {[V]} \ $のときに$ \ \mathrm {MOS} \ $トランジスタに流れる単位幅当たりの電流密度は$ \ \fbox {　（５）　} \ \mathrm {[A\cdot {cm}^{-1}]} \ $となる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　-3.1\times 10^{12}　　　　　&（ロ）&　-1.5\times 10^{0}　　　　　&（ハ）&　3.1\times 10^{-7} \\[ 5pt ] &（ニ）&　1.0\times 10^{-4}　　　　　&（ホ）&　2.0\times 10^{-2}　　　　　&（ヘ）&　1.0\times 10^{-1} \\[ 5pt ] &（ト）&　1.5\times 10^{0}　　　　　&（チ）&　2.0\times 10^{0}　　　　　&（リ）&　5.0\times 10^{0} \\[ 5pt ] &（ヌ）&　2.0\times 10^{1}　　　　　&（ル）&　2.0\times 10^{2}　　　　　&（ヲ）&　1.0\times 10^{4} \\[ 5pt ] &（ワ）&　2.0\times 10^{5}　　　　　&（カ）&　2.0\times 10^{6}　　　　　&（ヨ）&　3.1\times 10^{12} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

$ \ \mathrm {MOS} \ $トランジスタに流れる電流に関する問題です。
本問の場合は基本事項を理解している上で，問題文を理解して解けるようになる読解力が求められる問題です。$ \ 1 \ $種では受験生にその場で考えさせる問題が出題され戸惑う受験生も多いですが，慣れると確実に得点できる範囲となり得ますので問題慣れしておくようにしましょう。

1.$ \ \mathrm {n} \ $チャネル$ \ \mathrm {MOS} \ $トランジスタの動作
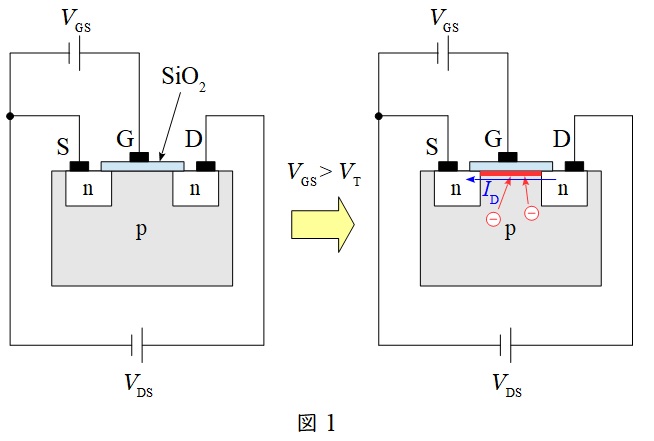
図1のように$ \ \mathrm {npn} \ $構造の半導体のゲート$ \ \left( \mathrm {G}\right) \ $に薄い絶縁膜$ \ \left( \mathrm {SiO_{2}}\right) \ $を取り付けたような構造をしたトランジスタです。
$ \ \mathrm {SiO_{2}} \ $は，絶縁体なので電子や正孔を通過させません。
ゲート電圧$ \ \left( V_{\mathrm {GS}}\right) \ $がしきい値電圧$ \ \left( V_{\mathrm {T}}\right) \ $よりも小さいときは，ドレイン－ソース間電圧$ \ \left( V_{\mathrm {DS}}\right) \ $をかけても，トランジスタ内の半導体接合部で逆電圧がかかる状態となるためトランジスタは導通しません。
ゲート電圧$ \ \left( V_{\mathrm {GS}}\right) \ $をしきい値電圧$ \ \left( V_{\mathrm {T}}\right) \ $よりも大きくすると，$ \ \mathrm {p} \ $形半導体内の少数キャリヤである電子が絶縁膜に引き寄せられ，疑似的に$ \ \mathrm {n} \ $形領域の通路ができ，ドレイン－ソース間電圧$ \ \left( V_{\mathrm {DS}}\right) \ $をかけると導通し，ドレイン電流$ \ \left( I_{\mathrm {D}}\right) \ $が流れるようになります。
ゲート電圧$ \ \left( V_{\mathrm {GS}}\right) \ $を大きくすると，$ \ \mathrm {n} \ $形領域の通路が大きくなるため，ドレイン電流$ \ \left( I_{\mathrm {D}}\right) \ $が増加することになります。

【解答】

(1)解答：ト
平行平板コンデンサの単位面積当たりの容量$ \ C \ \mathrm {[F]} \ $は，$ \ \mathrm {SiO_{2}} \ $の誘電率$ \ \varepsilon =3.4\times 10^{-13} \ \mathrm {[F\cdot {cm}^{-1}]} \ $，$ \ \mathrm {SiO_{2}} \ $の膜厚が$ \ d=1.0\times 10^{-6} \ \mathrm {[cm]} \ $であるから，
\[
\begin{eqnarray}
C&=&\frac {\varepsilon \times 1}{d} \\[ 5pt ] &=&\frac {3.4\times 10^{-13} \times 1}{1.0\times 10^{-6}} \\[ 5pt ] &=&3.4\times 10^{-7} \ \mathrm {[F]} \\[ 5pt ] \end{eqnarray}
\] となる。題意より，反転状態にある単位面積当たりの電子の面電荷密度$ \ \rho \ \mathrm {[C\cdot {cm}^{-2}]} \ $は，面積当たりの容量$ \ C \ \mathrm {[F]} \ $とオーバードライブ電圧$ \ \left( V_{\mathrm {G}}-V_{\mathrm {T}}\right) \ $との積になるので，
\[
\begin{eqnarray}
\rho &=&C\left( V_{\mathrm {G}}-V_{\mathrm {T}}\right) \\[ 5pt ] \end{eqnarray}
\] の関係がある。したがって，面電荷密度$ \ \rho =5.0\times 10^{-7} \ \mathrm {[C\cdot {cm}^{-2}]} \ $（※問題文は電子なので符号が逆となっていることに注意）とするために必要なオーバードライブ電圧$ \ \left( V_{\mathrm {G}}-V_{\mathrm {T}}\right) \ $は，
\[
\begin{eqnarray}
V_{\mathrm {G}}-V_{\mathrm {T}} &=&\frac {\rho }{C} \\[ 5pt ] &=&\frac {5.0\times 10^{-7}}{3.4\times 10^{-7}} \\[ 5pt ] &≒&1.4706\times 10^{0}　→　1.5\times 10^{0} \ \mathrm {[V]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ヨ
題意より，単位電荷$ \ e=1.6\times 10^{-19} \ \mathrm {[C]} \ $なので，電子のキャリヤ濃度$ \ N_{\mathrm {e}} \ \mathrm {[{cm}^{-2}]} \ $は，
\[
\begin{eqnarray}
N_{\mathrm {e}} &=&\frac {\rho }{e} \\[ 5pt ] &=&\frac {5.0\times 10^{-7}}{1.6\times 10^{-19}} \\[ 5pt ] &=&3.125\times 10^{12}　→　3.1\times 10^{12} \ \mathrm {[{cm}^{-2}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ル
電界の大きさ$ \ E \ $はチャネルの長さ$ \ d \ $，ドレーン－ソース間電圧$ \ V_{\mathrm {DS}} \ $とすると，
\[
\begin{eqnarray}
E &=&\frac {V_{\mathrm {DS}}}{d} \\[ 5pt ] \end{eqnarray}
\] で求められるので，$ \ d=5.0\times 10^{-4} \ \mathrm {[cm]} \ $，$ \ V_{\mathrm {DS}}=0.10 \ \mathrm {[V]} \ $であるとすれば，
\[
\begin{eqnarray}
E &=&\frac {0.10}{5.0\times 10^{-4}} \\[ 5pt ] &=&2.0\times 10^{2} \ \mathrm {[V\cdot {cm}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ワ
題意より，電子の速度$ \ v \ \mathrm {[cm\cdot {s}^{-1}]} \ $は，電子移動度$ \ \mu \ \mathrm {[{cm}^{2}\cdot {V}^{-1}\cdot {s}^{-1}]} \ $と電界の積$ \ E \ \mathrm {[V\cdot {cm}^{-1}]} \ $になるので，
\[
\begin{eqnarray}
v &=&\mu E \\[ 5pt ] \end{eqnarray}
\] となり，$ \ \mu =1.0\times 10^{3} \ \mathrm {[{cm}^{2}\cdot {V}^{-1}\cdot {s}^{-1}]} \ $，$ \ E=2.0\times 10^{2} \ \mathrm {[V\cdot {cm}^{-1}]} \ $を代入すると，
\[
\begin{eqnarray}
v &=&1.0\times 10^{3}\times 2.0\times 10^{2} \\[ 5pt ] &=&2.0\times 10^{5} \ \mathrm {[cm\cdot {s}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヘ
題意より，電流密度$ \ J \ \mathrm {[A\cdot {cm}^{-1}]} \ $は面電荷密度$ \ \rho \ \mathrm {[C\cdot {cm}^{-2}]} \ $と速度$ \ v \ \mathrm {[cm\cdot {s}^{-1}]} \ $の積となるので，$ \ \rho =5.0\times 10^{-7} \ \mathrm {[C\cdot {cm}^{-2}]} \ $，$ \ v=2.0\times 10^{5} \ \mathrm {[cm\cdot {s}^{-1}]} \ $を代入すると，
\[
\begin{eqnarray}
J &=&\rho v \\[ 5pt ] &=&5.0\times 10^{-7}\times 2.0\times 10^{5} \\[ 5pt ] &=&1.0\times 10^{-1} \ \mathrm {[A\cdot {cm}^{-1}]} \\[ 5pt ] \end{eqnarray}
\] と求められる。