【問題】
【難易度】★★★★☆(やや難しい)
次の文章は,\( \ RC \ \)回路に関する記述である。文中の\( \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ \)に当てはまるものを解答群の中から選びなさい。
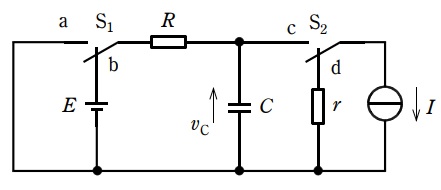
図のようにスイッチ\( \ \mathrm {S}_{1} \ \),\( \ \mathrm {S}_{2} \ \)と直流電圧源\( \ E \ \),直流電流源\( \ I \ \),抵抗\( \ R \ \),\( \ r \ \),静電容量\( \ C \ \)が接続されている。静電容量\( \ C \ \)の両端の電圧を図のように定める。
時間\( \ t<0 \ \)では,スイッチ\( \ \mathrm {S}_{1} \ \)は\( \ \mathrm {b} \ \)側,スイッチ\( \ \mathrm {S}_{2} \ \)は\( \ \mathrm {d} \ \)側であり,回路は定常状態である。\( \ t=0 \ \)において\( \ \mathrm {S}_{1} \ \)を\( \ \mathrm {a} \ \)側,\( \ \mathrm {S}_{2} \ \)を\( \ \mathrm {c} \ \)側に切り替えた。
\( \ t>0 \ \)における静電容量\( \ C \ \)の両端の電圧\( \ v_{\mathrm {c}} \ \)の時間的変化について考える。このとき,\( \ R \ \)の両端の電圧と\( \ C \ \)の両端の電圧は等しいこと,及び初期値を考慮すると,
\[
\begin{eqnarray}
v_{\mathrm {c}} &=& \fbox { (1) } \\[ 5pt ]
\end{eqnarray}
\]
となる。
\( \ v_{\mathrm {c}} \ \)が\( \ 0 \ \mathrm {[V]} \ \)になった時刻\( \ T_{1} \ \)において\( \ \mathrm {S}_{1} \ \)を\( \ \mathrm {a} \ \)側から\( \ \mathrm {b} \ \)側に切り替えた。
\[
\begin{eqnarray}
T_{1} &=& \fbox { (2) } \\[ 5pt ]
\end{eqnarray}
\]
となる。
\( \ t>T_{1} \ \)における\( \ v_{\mathrm {c}} \ \)は,電圧源による過渡応答と電流源による過渡応答との重ね合わせになるので,
\[
\begin{eqnarray}
v_{\mathrm {c}} &=& \fbox { (3) }+\fbox { (1) } \\[ 5pt ]
\end{eqnarray}
\]
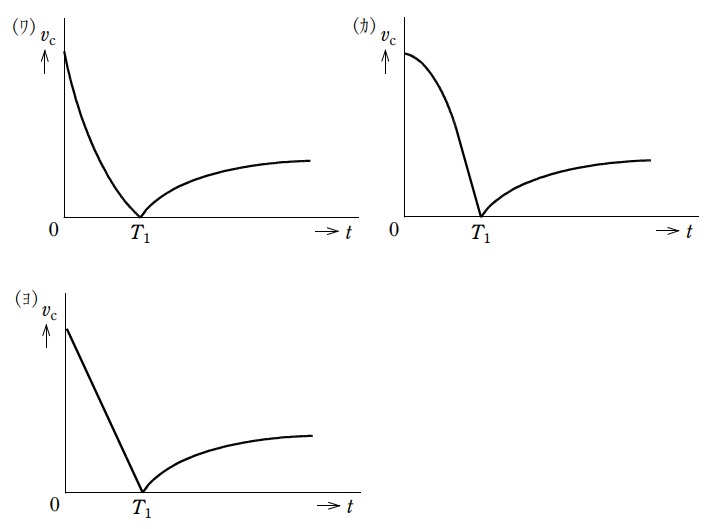
となり,\( \ t=\infty \ \)における\( \ v_{\mathrm {c}} \ \)は\( \ \fbox { (4) } \ \)となる。\( \ \fbox { (4) }>0 \ \)のとき,\( \ v_{\mathrm {c}} \ \)の変化の様子を表す図は\( \ \fbox { (5) } \ \)である。
〔問3の解答群〕
\[
\begin{eqnarray}
&(イ)& E-\frac {I}{C}t &(ロ)& CR\ln \left( 1+\frac {E}{RI} \right) &(ハ)& -RI+\left(RI+E\right)\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
&(ニ)& CR\ln \left| \frac {RI}{RI-E}\right| &(ホ)& E\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) &(ヘ)& RI-E \\[ 5pt ]
&(ト)& E\left( 1-\mathrm {e}^{-\frac {t-T_{1}}{CR}}\right) &(チ)& E\mathrm {e}^{-\frac {t-T_{1}}{CR}} &(リ)& E-RI \\[ 5pt ]
&(ヌ)& E-RI\left( 1-\mathrm {e}^{-\frac {t}{CR}}\right) &(ル)& \frac {EC}{I} &(ヲ)& E-RI+\frac {I}{C} \\[ 5pt ]
\end{eqnarray}
\]
【ワンポイント解説】
過渡現象に関する問題です。回路が電流源なので,回路方程式を\( \ \displaystyle \frac {\mathrm {d}i}{\mathrm {d}t} \ \)ではなく\( \ \displaystyle \frac {\mathrm {d}v}{\mathrm {d}t} \ \)で記載する必要があります。
1.過渡現象における\( \ RLC \ \)それぞれの電流
各インピーダンスに電圧\( \ v \ \)をかけた時,抵抗\( \ R \ \)の電流\( \ i_{\mathrm {R}} \ \),リアクトル\( \ L \ \)の電流\( \ i_{\mathrm {L}} \ \),コンデンサ\( \ C \ \)の電流\( \ i_{\mathrm {C}} \ \)とすると,
\[
\begin{eqnarray}
i_{\mathrm{R}} &=& \frac {v}{R} \\[ 5pt ]
i_{\mathrm{L}} &=& \frac {1}{L}\int v \mathrm {d}t \\[ 5pt ]
i_{\mathrm{C}} &=& C\frac {\mathrm {d}v}{\mathrm {d}t}\\[ 5pt ]
\end{eqnarray}
\]
となります。
2.過渡現象における定常解と過渡解
ⅰ.定常解を\( \ i_{\mathrm {s}} \ \),過渡解を\( \ i_{\mathrm {t}} \ \)とすると,電流値\( \ i \ \)は\( \ =i_{\mathrm {s}}+i_{\mathrm {t}} \ \)となります。
ⅱ.定常解は電流の時間変化のない状態すなわち\( \ \displaystyle \frac {\mathrm {d}i_{\mathrm {s}}}{\mathrm {d}t}=0 \ \)とした時の解です。
ⅲ.過渡解はスイッチを入れた直後の解です。
3.自然対数の微分積分
①自然対数の微分
\[
\begin{eqnarray}
\frac {\mathrm {d}}{\mathrm {d}x} \ln {x} &=&\frac {1}{x} \\[ 5pt ]
\end{eqnarray}
\]
②自然対数の積分
\[
\begin{eqnarray}
\int \frac {1}{x} &=&\ln {x} + C \left( Cは積分定数\right) \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
\ln {x} &=&-\alpha t +C \left( Cは積分定数\right)の時, x=A\mathrm {e}^{-\alpha t} \left( A=\mathrm {e}^{C}\right)となります。 \\[ 5pt ]
\end{eqnarray}
\]
【関連する「電気の神髄」記事】
【解答】
(1)解答:ハ
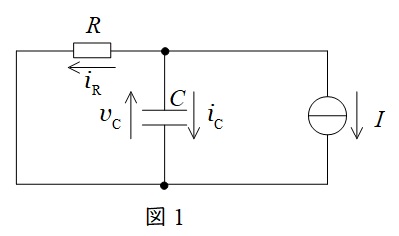
\( \ t>0 \ \)における回路は図1のようになる。
図1のように各電流の方向を定めると,
\[
\begin{eqnarray}
i_{\mathrm {C}}+i_{\mathrm {R}}+I&=&0 \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ t>0 \ \)において,ワンポイント解説「1.過渡現象における\( \ RLC \ \)それぞれの電流」の通り,
\[
\begin{eqnarray}
C\frac {\mathrm {d}v_{\mathrm {C}}}{\mathrm {d}t}+\frac {v_{\mathrm {C}}}{R}+I&=&0 \\[ 5pt ]
C\frac {\mathrm {d}v_{\mathrm {C}}}{\mathrm {d}t}+\frac {v_{\mathrm {C}}}{R}&=&-I \\[ 5pt ]
\end{eqnarray}
\]
となる。ここで,\( \ v_{\mathrm {C}} \ \)の定常解を\( \ v_{\mathrm {Cs}} \ \),過渡解を\( \ v_{\mathrm {Ct}} \ \)とすると,
\[
\begin{eqnarray}
\frac {v_{\mathrm {Cs}}}{R}&=&-I \\[ 5pt ]
v_{\mathrm {Cs}}&=&-RI \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
C\frac {\mathrm {d}v_{\mathrm {Ct}}}{\mathrm {d}t}+\frac {v_{\mathrm {Ct}}}{R}&=&0 \\[ 5pt ]
C\frac {\mathrm {d}v_{\mathrm {Ct}}}{\mathrm {d}t}&=&-\frac {v_{\mathrm {Ct}}}{R} \\[ 5pt ]
\frac {1}{v_{\mathrm {Ct}}}\mathrm {d}v_{\mathrm {Ct}}&=&-\frac {1}{CR}\mathrm {d}t \\[ 5pt ]
v_{\mathrm {Ct}}&=&A\mathrm {e}^{-\frac {t}{CR}} ( Aは積分定数) \\[ 5pt ]
\end{eqnarray}
\]
となるので,一般解は,
\[
\begin{eqnarray}
v_{\mathrm {C}}&=&v_{\mathrm {Cs}}+v_{\mathrm {Ct}} \\[ 5pt ]
&=&-RI+A\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
となる。\( \ t=0 \ \)におけるコンデンサ電圧\( \ v_{\mathrm {C0}}=E \ \)であるから,
\[
\begin{eqnarray}
E&=&-RI+A \\[ 5pt ]
A&=&E+RI
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
v_{\mathrm {C}}&=&-RI+\left( E+RI\right) \mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(2)解答:ロ
\( \ v_{\mathrm {c}} \ \)が\( \ 0 \ \mathrm {[V]} \ \)になった時刻\( \ T_{1} \ \)は,
\[
\begin{eqnarray}
0&=&-RI+\left( E+RI\right) \mathrm {e}^{-\frac {T_{1}}{CR}} \\[ 5pt ]
RI&=&\left( E+RI\right) \mathrm {e}^{-\frac {T_{1}}{CR}} \\[ 5pt ]
\frac {RI}{E+RI}&=&\mathrm {e}^{-\frac {T_{1}}{CR}} \\[ 5pt ]
\mathrm {e}^{\frac {T_{1}}{CR}}&=&\frac {E+RI}{RI} \\[ 5pt ]
\frac {T_{1}}{CR}&=&\ln \left( 1+\frac {E}{RI}\right) \\[ 5pt ]
T_{1}&=&CR\ln \left( 1+\frac {E}{RI}\right) \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
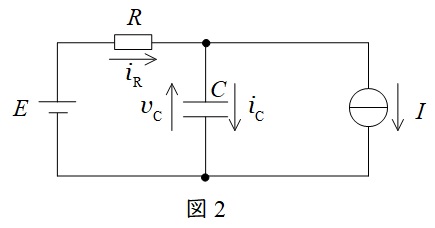
(3)解答:ト
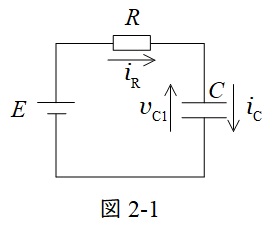
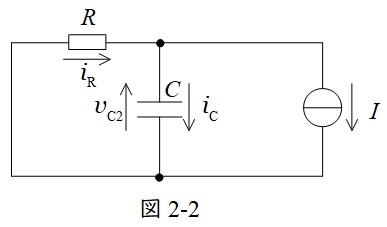
\( \ t>T_{1} \ \)において,回路は図2のようになる。図2は重ね合わせの理により図2-1及び図2-2に分解でき,\( \ v_{\mathrm {C}}=v_{\mathrm {C1}}+v_{\mathrm {C2}} \ \)で求められる。
図2-1において,回路方程式は,
\[
\begin{eqnarray}
Ri_{\mathrm {R}}+\frac {1}{C}\int i_{\mathrm {C}} \mathrm {d}t&=&E \\[ 5pt ]
Ri_{\mathrm {C}}+\frac {1}{C}\int i_{\mathrm {C}} \mathrm {d}t&=&E \\[ 5pt ]
R\frac {\mathrm {d}q_{\mathrm {C}}}{\mathrm {d}t}+\frac {q_{\mathrm {C}}}{C}&=&E \\[ 5pt ]
\end{eqnarray}
\]
であり,(1)と同様に定常解\( \ q_{\mathrm {Cs}} \ \),過渡解\( \ q_{\mathrm {Ct}} \ \)から解を求めると,
\[
\begin{eqnarray}
\frac {q_{\mathrm {Cs}}}{C}&=&E \\[ 5pt ]
q_{\mathrm {Cs}}&=&CE \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
R\frac {\mathrm {d}q_{\mathrm {Ct}}}{\mathrm {d}t}+\frac {q_{\mathrm {Ct}}}{C}&=&0 \\[ 5pt ]
q_{\mathrm {Ct}}&=&A\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
\[
\begin{eqnarray}
q_{\mathrm {C}}&=&q_{\mathrm {Cs}}+q_{\mathrm {Ct}} \\[ 5pt ]
&=&CE+A\mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
となり,\( \ t=T_{1} \ \)で\( \ q_{\mathrm {C}}=0 \ \)であるので,
\[
\begin{eqnarray}
0&=&CE+A\mathrm {e}^{-\frac {T_{1}}{CR}} \\[ 5pt ]
A&=&-CE\mathrm {e}^{\frac {T_{1}}{CR}}
\end{eqnarray}
\]
となり,
\[
\begin{eqnarray}
q_{\mathrm {C}}&=&CE\left( 1-\mathrm {e}^{\frac {T_{1}}{CR}}\mathrm {e}^{-\frac {t}{CR}}\right) \\[ 5pt ]
&=&CE\left( 1-\mathrm {e}^{-\frac {t-T_{1}}{CR}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {C1}}&=&\frac {q_{\mathrm {C}}}{C} \\[ 5pt ]
&=&E\left( 1-\mathrm {e}^{-\frac {t-T_{1}}{CR}}\right) \\[ 5pt ]
\end{eqnarray}
\]
となる。一方,図2-2において,(1)で求めたように,
\[
\begin{eqnarray}
v_{\mathrm {C2}}&=&-RI+\left( E+RI\right) \mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
となるので,
\[
\begin{eqnarray}
v_{\mathrm {C}}&=&v_{\mathrm {C1}}+v_{\mathrm {C2}} \\[ 5pt ]
&=&E\left( 1-\mathrm {e}^{-\frac {t-T_{1}}{CR}}\right) -RI+\left( E+RI\right) \mathrm {e}^{-\frac {t}{CR}} \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(4)解答:リ
(3)の解答式において,\( \ t=\infty \ \)とすると,
\[
\begin{eqnarray}
v_{\mathrm {C}}&=&E\left( 1-0\right) -RI+\left( E+RI\right) \times 0 \\[ 5pt ]
&=&E-RI \\[ 5pt ]
\end{eqnarray}
\]
と求められる。
(5)解答:ワ
(1),(3)より,電圧は指数関数的に変化するため,最も適当な図は(ワ)となる。






















 愛知県出身 愛称たけちゃん
愛知県出身 愛称たけちゃん