《理論》〈電磁気〉[H25:問6] 電流が作る磁界に関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，電流が作る磁界に関するに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまるものを解答群の中から選びなさい。

透磁率$ \ \mu _{0} \ $の真空中において，半径$ \ R \ $の円環状の回路に流れる電流$ \ I \ $が円環中心点に作る磁束密度の大きさは$ \ \fbox {　（１）　} \ $である。これを，ビオ・サバールの法則を用いて導出することを考える。

まず，図1に示すような長さ$ \ 2l \ $の線分$ \ \mathrm {A}－\mathrm {B} \ $の部分を流れる電流$ \ I \ $が点$ \ \mathrm {O} \ $にもたらす磁界の大きさを求める。このとき，点$ \ \mathrm {O} \ $は点$ \ \mathrm {A} \ $及び点$ \ \mathrm {B} \ $から等距離にあり，線分$ \ \mathrm {A}－\mathrm {B} \ $から距離$ \ a \ $の位置にあるとする。また，線分$ \ \mathrm {A}－\mathrm {B} \ $上に図1に示すように$ \ x \ $軸を考える。

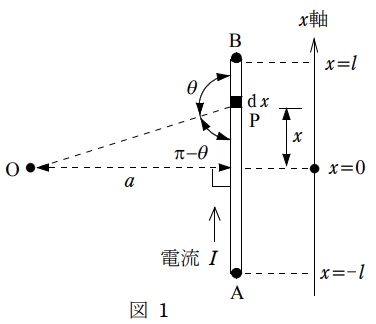
線分$ \ \mathrm {A}－\mathrm {B} \ $上の点$ \ \mathrm {P} \ $について，$ \ x \ $を$ \ a \ $と$ \ \theta \ $を用いて表すと，$ \ x=\fbox {　（２）　} \ $と表すことができる。このとき，$ \ \cos \theta =-\cos \left( \pi -\theta \right) \ $であることなどを参考とされたい。よって，これを$ \ \theta \ $で微分することにより，次式を得る。
\[
\begin{eqnarray}
\frac {\mathrm {d}x}{\mathrm {d}\theta } &=& \fbox {　（３）　} \\[ 5pt ] \end{eqnarray}
\] ここで，微小部分$ \ \mathrm {d}x \ $を流れる電流$ \ I \ $が点$ \ \mathrm {O} \ $に作る磁束密度は，線分$ \ \mathrm {O}－\mathrm {P} \ $の長さを$ \ r \ $とすると，ビオ・サバールの法則により，次式で与えられる。
\[
\begin{eqnarray}
\mathrm {d}B &=& \frac {\mu _{0}}{4\pi }\frac {I\mathrm {d}x\sin \theta }{r^{2} } &=&\frac {\mu _{0}I}{4\pi }\fbox {　（４）　} \ \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] $ \ ∠\mathrm {OAB}=∠\mathrm {OBA}=\theta _{1} \ $とすると，線分$ \ \mathrm {A}－\mathrm {B} \ $全体を流れる電流$ \ I \ $が点$ \ \mathrm {O} \ $に作る磁束密度は，これを積分して，次式のように求まる。
\[
\begin{eqnarray}
B_{\mathrm {AB}} &=& \int _{\theta _{1}}^{\pi -\theta _{1}}\frac {\mu _{0}I}{4\pi }\fbox {　（４）　} \ \mathrm {d}\theta = \fbox {　（５）　}\\[ 5pt ] \end{eqnarray}
\] ただし，$ \ \displaystyle \cos \theta _{1}=\frac {l}{\sqrt {a^{2}+l^{2}}} \ $であることを用いた。

次にこれを用いて，図2に示すような，半径$ \ R \ $の円に内接する正$ \ n \ $角形状の電気回路に流れる電流$ \ I \ $が，その中心点$ \ \mathrm {O} \ $に作る磁束密度を求める。

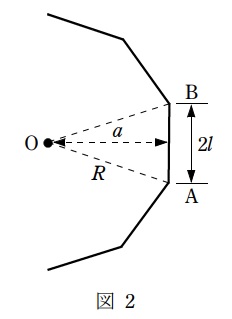
線分$ \ \mathrm {A}－\mathrm {B} \ $の部分が点$ \ \mathrm {O} \ $に作る磁束密度$ \ B_{\mathrm {AB}} \ $を$ \ R \ $により表すことを考える。このとき，$ \ \fbox {　（５）　} \ $で求めた結果において，$ \ \displaystyle a=R\cos \frac {\pi}{n} \ $，$ \ \displaystyle l=R\sin \frac {\pi}{n} \ $と表すことができるから，$ \ \displaystyle B_{\mathrm {AB}}=\frac {\mu _{0}I}{2\pi R}\tan \frac {\pi}{n} \ $と求まる。

よって，これを$ \ n \ $倍することで，正$ \ n \ $角形状の電気回路に流れる電流$ \ I \ $が中央に作る磁束密度$ \ \displaystyle B_{\mathrm {total}} \ $を求めることができる。ここで，$ \ n→\infty \ $の極限値を考えると，$ \ \displaystyle B_{\mathrm {total}}=\fbox {　（１）　} \ $となり，円環状の回路に流れる電流が中心点に作る磁束密度の大きさと一致する。このとき，$ \displaystyle \lim_{ n \to \infty } \frac {\pi}{n}\tan \frac {\pi}{n}=1 \ $であることを用いた。

〔問6の解答群〕
\[
\begin{eqnarray}
&（イ）&　a\sin \theta　　&（ロ）&　\frac {\mu _{0}I}{2R}　　&（ハ）&　-a\frac {\sin \theta }{\cos \theta } \\[ 5pt ] &（ニ）&　-a\frac {\cos \theta }{\sin \theta }　　　&（ホ）&　\frac {I}{2\pi R}　　　&（ヘ）&　-\frac {a}{\cos ^{2}\theta } \\[ 5pt ] &（ト）&　\frac {\mu _{0}I}{2\pi R}　　　&（チ）&　\frac {a}{\sin ^{2}\theta }　　　&（リ）&　\frac {\mu _{0}Il}{2\pi a \sqrt {a^{2}+l^{2}}} \\[ 5pt ] &（ヌ）&　a\cos \theta　　　&（ル）&　\frac {\mu _{0}Il^{2}}{4\pi a \left( a^{2}+l^{2}\right) }　　　&（ヲ）&　\frac {\cos ^{2}\theta }{a} \\[ 5pt ] &（ワ）&　\frac {\sin \theta }{a}　　　&（カ）&　\frac {\cos \theta }{a}　　　&（ヨ）&　\frac {\mu _{0}Il}{4\pi a \sqrt {a^{2}+l^{2}}} \\[ 5pt ] \end{eqnarray}
\]

【ワンポイント解説】

ビオ・サバールの法則からアンペールの法則を導出する問題です。非常に良い練習問題となりますので，確実に理解しておくようにして下さい。

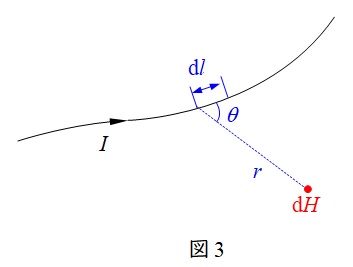
1.ビオ・サバールの法則
図3に示すように，微小な長さ$ \ \mathrm {d}l \ $に流れる電流$ \ I \ $が，距離$ \ r \ $離れた場所に作る磁界$ \ \mathrm {d} H \ $は，
\[
\begin{eqnarray}
\mathrm {d} H&=&\frac {I \mathrm {d}l}{4\pi r^{2}}\sin \theta \\[ 5pt ] \end{eqnarray}
\] となります。

2.磁束密度$ \ B \ $と磁界$ \ H \ $の関係
真空の透磁率を$ \ \mu _{0} \ $とすると，磁束密度$ \ B \ $と磁界$ \ H \ $には，
\[
\begin{eqnarray}
B &=& \mu _{0}H \\[ 5pt ] \end{eqnarray}
\] の関係があります。

【解答】

(1)解答：ロ
半径$ \ R \ $の円環状の回路に流れる電流$ \ I \ $が円環中心点に作る磁界$ \ H \ $の大きさは，
\[
\begin{eqnarray}
H&=&\frac {I}{2R} \\[ 5pt ] \end{eqnarray}
\] となり，ワンポイント解説「2.磁束密度$ \ B \ $と磁界$ \ H \ $の関係」の通り，磁束密度$ \ B \ $の大きさは，
\[
\begin{eqnarray}
B &=& \mu _{0}H \\[ 5pt ] &=& \frac {\mu _{0}I}{2R} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ニ
図1より，
\[
\begin{eqnarray}
a &=& x\tan \left( \pi -\theta \right) \\[ 5pt ] &=& x\frac {\sin \left( \pi -\theta \right) }{\cos \left( \pi -\theta \right) } \\[ 5pt ] \end{eqnarray}
\] であり，$ \ \sin \theta =\sin \left( \pi -\theta \right) \ $，$ \ \cos \theta =-\cos \left( \pi -\theta \right) \ $であるので，
\[
\begin{eqnarray}
a &=& x\frac {\sin \theta }{-\cos \theta } \\[ 5pt ] x &=& -a\frac {\cos \theta }{\sin \theta } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：チ
(3)の解答式を微分すると，
\[
\begin{eqnarray}
\frac {\mathrm {d}x}{\mathrm {d}\theta } &=& -a\frac {-\sin \theta \cdot \sin \theta-\cos \theta \cdot \cos \theta }{\sin ^{2}\theta } \\[ 5pt ] &=& a\frac {\sin ^{2}\theta +\cos ^{2}\theta }{\sin ^{2}\theta } \\[ 5pt ] &=& \frac {a}{\sin ^{2}\theta } \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：ワ
(3)の解答式及び題意より，微小部分$ \ \mathrm {d}x \ $を流れる電流$ \ I \ $が点$ \ \mathrm {O} \ $に作る磁束密度$ \ \mathrm {d}B \ $は，
\[
\begin{eqnarray}
\mathrm {d}B &=& \frac {\mu _{0}}{4\pi }\frac {I\mathrm {d}x\sin \theta }{r^{2} } \\[ 5pt ] &=&\frac {\mu _{0}}{4\pi }\frac {I\sin \theta }{a^{2}+x^{2} } \frac {a}{\sin ^{2}\theta }\mathrm {d}\theta \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi }\frac {a}{a^{2}+x^{2} } \frac {1}{\sin \theta }\mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] となり，$ \ \displaystyle \sin \theta =\frac {a}{\sqrt {a^{2}+x^{2}}} \ $であるので$ \ \displaystyle \frac {a}{a^{2}+x^{2}} =\frac {\sin ^{2}\theta }{a} \ $となり，
\[
\begin{eqnarray}
\mathrm {d}B &=&\frac {\mu _{0}I}{4\pi }\frac {\sin ^{2}\theta }{a} \frac {1}{\sin \theta }\mathrm {d}\theta \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi }\frac {\sin \theta }{a} \ \mathrm {d}\theta \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：リ
題意に沿って，(4)の解答式を積分すると，
\[
\begin{eqnarray}
B_{\mathrm {AB}} &=& \int _{\theta _{1}}^{\pi -\theta _{1}}\frac {\mu _{0}I}{4\pi }\frac {\sin \theta }{a} \ \mathrm {d}\theta \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi a} \int _{\theta _{1}}^{\pi -\theta _{1}}\sin \theta \ \mathrm {d}\theta \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi a} \left[ -\cos \theta \right] _{\theta _{1}}^{\pi -\theta _{1}} \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi a} \left[ -\cos \left( \pi -\theta _{1}\right) +\cos \theta _{1} \right] \\[ 5pt ] &=&\frac {\mu _{0}I}{4\pi a} \left[ \cos \theta _{1}+\cos \theta _{1} \right] \\[ 5pt ] &=&\frac {\mu _{0}I}{2\pi a} \cos \theta _{1} \\[ 5pt ] &=&\frac {\mu _{0}Il}{2\pi a \sqrt {a^{2}+l^{2}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。