《理論》〈電気回路〉[H30:問2] 非対称三相起電力を平衡三相負荷に接続した回路に関する計算問題

【問題】

【難易度】★☆☆☆☆（易しい）

次の文章は，非対称三相起電力を平衡三相負荷に接続した回路に関する記述である。文中の\(\fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$}\)に当てはまる最も適切なものを解答群の中から選べ。ただし，電圧，電流及びアドミタンスの単位は，それぞれ\( \ \mathrm {[V]} \ \)，\( \ \mathrm {[A]} \ \)及び\( \ \mathrm {[S]} \ \)とする。

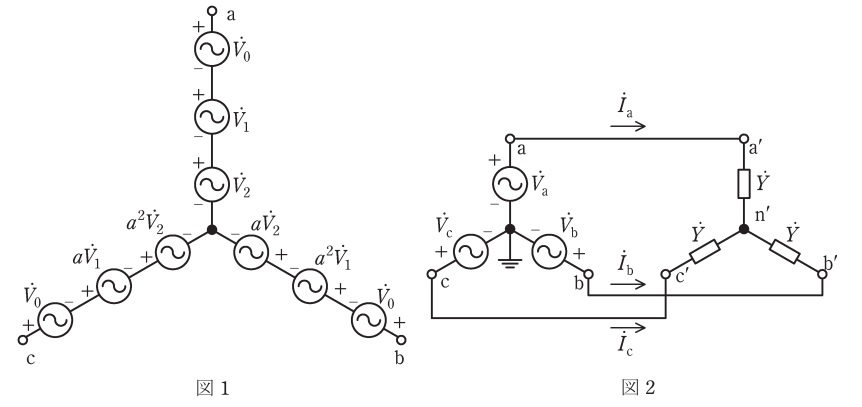
一般に非対称三相起電力\( ( \ {\dot V}_{\mathrm {a}}，{\dot V}_{\mathrm {b}}，{\dot V}_{\mathrm {c}} \ ) \)は図1に示すように対称三相起電力\( ( \ {\dot V}_{0}，{\dot V}_{1}，{\dot V}_{2} \ ) \)を用いて表すことができる。ここで，\( \ {\dot V}_{0}，{\dot V}_{1}，{\dot V}_{2} \ \)は\( \ {\dot V}_{\mathrm {a}}，{\dot V}_{\mathrm {b}}，{\dot V}_{\mathrm {c}} \ \)から，
\[
\begin{eqnarray}
\begin{pmatrix} {\dot V}_{0} \\ {\dot V}_{1} \\ {\dot V}_{2} \end{pmatrix} &=& \frac {1}{3}\begin{pmatrix} 1 & 1 & 1 \\ 1 & a & a^{2} \\ 1 & a^{2} & a \end{pmatrix}\begin{pmatrix} {\dot V}_{\mathrm {a}} \\ {\dot V}_{\mathrm {b}} \\ {\dot V}_{\mathrm {c}} \end{pmatrix} \\[ 5pt ] \end{eqnarray}
\] で導かれる。ただし，\( \ \displaystyle a=\mathrm {e}^{\mathrm {j}\frac {2\pi }{3}} \ \)である。

図2に示す非対称三相起電力\( ( \ {\dot V}_{\mathrm {a}}，{\dot V}_{\mathrm {b}}，{\dot V}_{\mathrm {c}} \ ) \)に\( \ \displaystyle \dot Y=\frac {1}{10} \ \)の平衡三相負荷を接続した回路を考える。\( \ {\dot V}_{\mathrm {a}}=100 \ \)，\( \ {\dot V}_{\mathrm {b}}=80a^{2} \ \)，\( \ {\dot V}_{\mathrm {c}}=120a \ \)のとき，\( \ {\dot V}_{0} \ \)，\( \ {\dot V}_{1} \ \)，\( \ {\dot V}_{2} \ \)はそれぞれ，\( \ {\dot V}_{0}=\fbox {　 （１） 　} \ \)，\( \ {\dot V}_{1}=\fbox {　 （２） 　} \ \)，\( \ {\dot V}_{2}=\displaystyle -\mathrm {j}\frac {20\sqrt {3}}{3} \ \)となる。このときの線電流は，零相分\( \ {\dot V}_{0} \ \)と正相分\( \ {\dot V}_{1} \ \)と逆相分\( \ {\dot V}_{2} \ \)の重ね合わせの理を用いることで求めることができる。零相分\( \ {\dot V}_{0} \ \)のみが存在する場合には点\( \ \mathrm {a}^{\prime } \ \)，点\( \ \mathrm {b}^{\prime } \ \)，点\( \ \mathrm {c}^{\prime } \ \)は等電位となるため回路に電流は流れず各線電流は零となる。一方，正相分\( \ {\dot V}_{1} \ \)のみが存在する場合の各線電流は，\( \ {\dot I}_{\mathrm {a1}}=\fbox {　 （２） 　}\dot Y \ \)，\( \ {\dot I}_{\mathrm {b1}}=\fbox {　 （２） 　}\dot Ya^{2} \ \)，\( \ {\dot I}_{\mathrm {c1}}=\fbox {　 （２） 　}\dot Ya \ \)となる。同様に，逆相分\( \ {\dot V}_{2} \ \)のみが存在する場合の各線電流は，\( \ \displaystyle {\dot I}_{\mathrm {a2}}=\dot Y {\dot V}_{2}=-\mathrm {j}\frac {2\sqrt{3}}{3} \ \)，\( \ \displaystyle {\dot I}_{\mathrm {b2}}=\dot Y a{\dot V}_{2}=1+\mathrm {j}\frac {\sqrt{3}}{3} \ \)，\( \ \displaystyle {\dot I}_{\mathrm {c2}}=\dot Y a^{2}{\dot V}_{2}=-1+\mathrm {j}\frac {\sqrt{3}}{3} \ \)となる。これより，図2の\( \ {\dot I}_{\mathrm {a}} \ \)と\( \ {\dot I}_{\mathrm {b}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=& {\dot I}_{\mathrm {a1}}+{\dot I}_{\mathrm {a2}} &=&\fbox {　 （３） 　} \\[ 5pt ] {\dot I}_{\mathrm {b}} &=& {\dot I}_{\mathrm {b1}}+{\dot I}_{\mathrm {b2}} &=&-4-\mathrm {j}\frac {14\sqrt{3}}{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。また，点\( \ \mathrm {n}^{\prime } \ \)でのキルヒホッフの電流則より，\( \ {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}}=\fbox {　 （４） 　} \ \)であることを考慮すると，\( \ {\dot I}_{\mathrm {c}}=\fbox {　 （５） 　} \ \)が求められる。

〔問2の解答群〕
\[
\begin{eqnarray}
&（イ）&　\mathrm {j}20\sqrt {3}　　　&（ロ）&　14+\mathrm {j}\frac {16\sqrt {3}}{3}　　　&（ハ）&　10 \\[ 5pt ] &（ニ）&　-100　　　&（ホ）&　100-\mathrm {j}\frac {2\sqrt {3}}{3}　　　&（ヘ）&　10-\mathrm {j}\frac {2\sqrt {3}}{3} \\[ 5pt ] &（ト）&　100　　　&（チ）&　1　　　&（リ）&　\mathrm {j}\frac {40\sqrt {3}}{3} \\[ 5pt ] &（ヌ）&　\mathrm {j}\frac {20\sqrt {3}}{3}　　　&（ル）&　300　　　&（ヲ）&　-6+\mathrm {j}\frac {16\sqrt {3}}{3} \\[ 5pt ] &（ワ）&　-6-\mathrm {j}\frac {20\sqrt {3}}{3}　　　&（カ）&　0　　　&（ヨ）&　-10-\mathrm {j}\frac {2\sqrt {3}}{3}
\end{eqnarray}
\]

【ワンポイント解説】

この問題は対称座標法を利用した三相回路の問題ですが，実質数学の問題であると考えて良いと思います。数値を代入して計算するだけなので，一種レベルの受験生であればほとんどの受験生が完答されたと思います。ベクトルオペレータは過去問でも何度も扱われている内容なので，確実にマスターしておいて下さい。

1.ベクトルオペレータ\(a\)
題意で与えられているベクトルオペレータ\(a=\mathrm {e}^{\mathrm {j}\frac {2\pi}{3}}\)は，
\[
\begin{eqnarray}
a &=& \cos \frac {2\pi}{3}+\mathrm {j}\sin \frac {2\pi}{3} &=& -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{2} &=& \cos \frac {4\pi}{3}+\mathrm {j}\sin \frac {4\pi}{3} &=& -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2} \\[ 5pt ] a^{3} &=& \cos \frac {6\pi}{3}+\mathrm {j}\sin \frac {6\pi}{3} &=& 1 \\[ 5pt ] \end{eqnarray}
\] となります。したがって，
\[
\begin{eqnarray}
1+a+a^{2} &=& 0 \\[ 5pt ] \end{eqnarray}
\] が成立します。

【関連する「電気の神髄」記事】

　　対称座標法変換の基本式

【解答】

(1)解答：ヌ
題意より，
\[
\begin{eqnarray}
{\dot V}_{0} &=& \frac {1}{3}\left( {\dot V}_{\mathrm {a}}+{\dot V}_{\mathrm {b}}+{\dot V}_{\mathrm {c}}\right) \\[ 5pt ] &=& \frac {1}{3}\times \left( 100+80a^{2}+120a\right) \\[ 5pt ] &=& \frac {1}{3}\times \left[ 100+80\times \left( -\frac {1}{2}-\mathrm {j}\frac {\sqrt {3}}{2}\right) +120\times\left( -\frac {1}{2}+\mathrm {j}\frac {\sqrt {3}}{2}\right) \right] \\[ 5pt ] &=& \frac {1}{3}\times \left( 100-40-\mathrm {j}40\sqrt {3} -60+\mathrm {j}60\sqrt {3}\right) \\[ 5pt ] &=& \mathrm {j}\frac {20\sqrt {3}}{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ト
題意より，
\[
\begin{eqnarray}
{\dot V}_{1} &=& \frac {1}{3}\left( {\dot V}_{\mathrm {a}}+a{\dot V}_{\mathrm {b}}+a^{2}{\dot V}_{\mathrm {c}}\right) \\[ 5pt ] &=& \frac {1}{3}\times \left( 100+a\times 80a^{2}+a^{2}\times 120a\right) \\[ 5pt ] &=& \frac {1}{3}\times \left( 100+80a^{3}+120a^{3}\right) \\[ 5pt ] &=& \frac {1}{3}\times \left( 100+80+120\right) \\[ 5pt ] &=& 100 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(3)解答：ヘ
(2)より，\( \ {\dot I}_{\mathrm {a1}} \ \)及び\( \ {\dot I}_{\mathrm {a2}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a1}} &=& \dot Y{\dot V}_{1} \\[ 5pt ] &=& \frac {1}{10}\times 100 \\[ 5pt ] &=& 10 \\[ 5pt ] \end{eqnarray}
\] \[
\begin{eqnarray}
{\dot I}_{\mathrm {a2}} &=& \dot Y{\dot V}_{2} \\[ 5pt ] &=& \frac {1}{10}\times \left( -\mathrm {j}\frac {20\sqrt {3}}{3}\right) \\[ 5pt ] &=& -\mathrm {j}\frac {2\sqrt {3}}{3} \\[ 5pt ] \end{eqnarray}
\] であるから，\( \ {\dot I}_{\mathrm {a}} \ \)は，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}} &=& {\dot I}_{\mathrm {a1}}+{\dot I}_{\mathrm {a2}} \\[ 5pt ] &=& 10-\mathrm {j}\frac {2\sqrt {3}}{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(4)解答：カ
図2において，キルヒホッフの法則より，三相の電流和が零でなければならないので，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}+{\dot I}_{\mathrm {c}} &=& 0 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヲ
(3)，(4)より，
\[
\begin{eqnarray}
{\dot I}_{\mathrm {c}} &=& -\left( {\dot I}_{\mathrm {a}}+{\dot I}_{\mathrm {b}}\right) \\[ 5pt ] &=& -\left( 10-\mathrm {j}\frac {2\sqrt {3}}{3}-4-\mathrm {j}\frac {14\sqrt{3}}{3}\right) \\[ 5pt ] &=& -\left( 6-\mathrm {j}\frac {16\sqrt {3}}{3}\right) \\[ 5pt ] &=& -6+\mathrm {j}\frac {16\sqrt {3}}{3} \\[ 5pt ] \end{eqnarray}
\] と求められる。