《理論》〈電子回路〉[H27:問4] npnバイポーラトランジスタに関する計算問題

1 【問題】
2 【ワンポイント解説】
3 【解答】

【問題】

【難易度】★★★★☆（やや難しい）

次の文章は，$ \ \mathrm {npn} \ $バイポーラトランジスタに関する記述である。文中の$ \ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。ただし，$ \ k \ $はボルツマン定数，$ \ T \ $は温度，$ \ q \ $は単位電荷である。

半導体の正孔のキャリヤ密度$ \ p \ $と電子のキャリヤ密度$ \ n \ $には平衡状態で$ \ pn \ $積一定という関係が成立し，さらに$ \ p=n \ $では物質で決まる定数である真性キャリヤ密度$ \ n_{\mathrm {i}} \ $を用いて$ \ p=n=n_{\mathrm {i}} \ $となる。そこで，不純物ドーピング密度と同じになる多数キャリヤ密度が決まると平衡時の小数キャリヤ密度も決まる。

$ \ \mathrm {npn} \ $バイポーラトランジスタのベースドーピング密度は$ \ N_{\mathrm {B}} \ $である。すると平衡時のベースの小数キャリヤ密度は$ \ n_{\mathrm {B0}}= \ \fbox {　（１）　} \ $となる。ここで，エミッタを接地し，ベースは電圧$ \ V_{\mathrm {B}} \ $に，コレクタは電圧$ \ V_{\mathrm {C}} \ $にバイアスしたとし，$ \ 0 ＜ V_{\mathrm {B}} ＜ V_{\mathrm {C}} \ $とする。ベース層厚が$ \ W \ $のとき，$ \ x=0 \ $をエミッタ側端，$ \ x=W \ $をコレクタ側端とするベース内の位置$ \ x \ $の関数としてベース層内小数キャリヤ密度を$ \ n_{\mathrm {B}}(x) \ $と表すものとする。エミッタに隣接した場所でのベース層内小数キャリヤ密度はエミッタ側から注入される電子により非平衡となり，$ \ n_{\mathrm {B}}(0)= \ \fbox {　（２）　} \ $となる。同様にコレクタに隣接した場所でのベース層内小数キャリヤ密度は通常のバイアス条件では，コレクタへ電子が急速に流れ出ることにより$ \ n_{\mathrm {B}}(W)=0 \ $とみなせる。

ベース層内でキャリヤ密度に非平衡があるので，電子は拡散してエミッタ側からコレクタ側へ向かう。ベース中の再結合を無視できるとすると密度勾配は一定になり，$ \ n_{\mathrm {B}}(x)=\fbox {　（３）　} \ $と表され，密度勾配は$ \ \fbox {　（４）　} \ $となる。電子の流れは，密度勾配に拡散定数$ \ D_{\mathrm {nB}} \ $を掛けたものとなり，ベースから流れ出た電子の流れはそのままコレクタ電流となるので，電子の流れに電子の電荷$ \ -q \ $を掛けるとコレクタ電流密度は$ \ \fbox {　（５）　} \ $となる。

〔問4の解答群〕
\[
\begin{eqnarray}
&（イ）&　\frac {n_{\mathrm {B}}(0)(W-x)}{W}　　　　　&（ロ）&　-\frac {n_{\mathrm {B0}}}{W}　　　　　&（ハ）&　n_{\mathrm {B0}}\exp \left( \frac {qV_{\mathrm {B}}}{kT}\right) \\[ 5pt ] &（ニ）&　qD_{\mathrm {nB}}n_{\mathrm {B}}(0)　　　　　&（ホ）&　-\frac {n_{\mathrm {B}}(0)}{W}　　　　　&（ヘ）&　-\frac {N_{\mathrm {B}}}{W} \\[ 5pt ] &（ト）&　n_{\mathrm {B0}}\exp \left( \frac {qV_{\mathrm {C}}}{kT}\right) 　　　　　&（チ）&　n_{\mathrm {B0}}\exp \left[ \frac {q\left( V_{\mathrm {B}}-V_{\mathrm {C}}\right) }{kT}\right] 　　　　　&（リ）&　\frac {n_{\mathrm {i}}^{2}}{N_{\mathrm {B}}} \\[ 5pt ] &（ヌ）&　\frac {qD_{\mathrm {nB}}n_{\mathrm {B}}(0)}{W}　　　　　&（ル）&　n_{\mathrm {i}}　　　　　&（ヲ）&　N_{\mathrm {B}} \\[ 5pt ] &（ワ）&　\frac {qn_{\mathrm {B}}(0)}{W}　　　　　&（カ）&　\frac {n_{\mathrm {B}}(0)x}{W}　　　　　&（ヨ）&　n_{\mathrm {B}}(0)\exp \left( \frac {W-x}{W}\right)
\end{eqnarray}
\]

【ワンポイント解説】

電子回路の中身の原理に関する出題で，電子回路の専門書に記載されているような内容です。電験としてはかなり難しい問題ですが，一種受験者であれば様々な知識も豊富だと思いますので，(3)以降は何とか想像力を働かせて解いて欲しいです。

1.$ \ \mathrm {npn} \ $バイポーラトランジスタの構造と原理
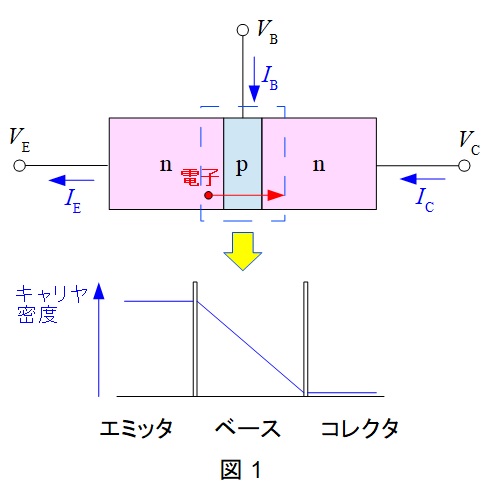
図1に示すように，$ \ \mathrm {npn} \ $バイポーラトランジスタは，二個の$ \ \mathrm {n} \ $層と薄い$ \ \mathrm {p} \ $層で構成されており，$ \ 0 ＜ V_{\mathrm {B}} ＜ V_{\mathrm {C}} \ $となる電圧をかけると，エミッタ層にある多数キャリヤの電子がコレクタ側に移動して電流が流れます。
ベース層を通る電子は一部正孔に吸収されますが，ベース層が非常に薄いことと，ベース電流がコレクタ電流に比べ非常に小さいので，無視することができると仮定すれば，$ \ \mathrm {p} \ $層近傍の電子の濃度分布は図1の下のようになります。

【解答】

(1)解答：リ
題意より，平衡状態では$ \ pn \ $積一定で$ \ p=n=n_{\mathrm {i}} \ $となるので，
\[
pn=n_{\mathrm {i}}^{2}
\] となる。また，ベース層のベースドーピング密度は正孔のドーピング密度となるので，
\[
\begin{eqnarray}
N_{\mathrm {B}}n_{\mathrm {B0}}&=&n_{\mathrm {i}}^{2} \\[ 5pt ] n_{\mathrm {B0}}&=&\frac {n_{\mathrm {i}}^{2}}{N_{\mathrm {B}}} \\[ 5pt ] \end{eqnarray}
\] と求められる。

(2)解答：ハ
$ \ x=0 \ $での小数キャリヤ密度の濃度はボルツマン分布則に従うので，
\[
n_{\mathrm {B}}(0)=n_{\mathrm {B0}}\exp \left( \frac {qV_{\mathrm {B}}}{kT}\right)
\] と求められる。

(3)解答：イ
(4)解答：ホ
キャリヤ密度は$ \ x=0 \ $のとき$ \ n_{\mathrm {B}}(0) \ $，$ \ x=W \ $のとき$ \ 0 \ $となるので，その傾きは，
\[
-\frac {n_{\mathrm {B}}(0)}{W}
\] となるので，密度分布は，
\[
\begin{eqnarray}
n_{\mathrm {B}}(x)&=&-\frac {n_{\mathrm {B}}(0)}{W}x+n_{\mathrm {B}}(0) \\[ 5pt ] &=&\frac {n_{\mathrm {B}}(0)(W-x)}{W}　 \\[ 5pt ] \end{eqnarray}
\] と求められる。

(5)解答：ヌ
題意より電子の流れは密度勾配に拡散定数$ \ D_{\mathrm {nB}} \ $を掛けたもので，電子の流れに電子の電荷$ \ -q \ $を掛けるとコレクタ電流密度$ \ i_{\mathrm {C}} \ $となるので，
\[
\begin{eqnarray}
i_{\mathrm {C}}&=&-\frac {n_{\mathrm {B}}(0)}{W}\times D_{\mathrm {nB}}\times \left( -q\right) \\[ 5pt ] &=&\frac {qD_{\mathrm {nB}}n_{\mathrm {B}}(0)}{W} \\[ 5pt ] \end{eqnarray}
\] と求められる。