《理論》〈電子回路〉[H27:問7] 演算増幅器を用いた回路に関する計算問題

【問題】

【難易度】★★☆☆☆（やや易しい）

次の文章は，演算増幅器を用いた回路に関する記述である。文中の$\ \fbox{$\hskip3em\Rule{0pt}{0.8em}{0em}$} \ $に当てはまる最も適切なものを解答群の中から選びなさい。ただし，演算増幅器の電圧増幅度(差動利得)は周波数とは無関係に無限大であり，また，入力インピーダンスは無限大，出力インピーダンスは零とする。入力信号源$\ v_{1} \ $と$\ v_{2} \ $は角周波数$\ \omega \ $の正弦波電圧源である。

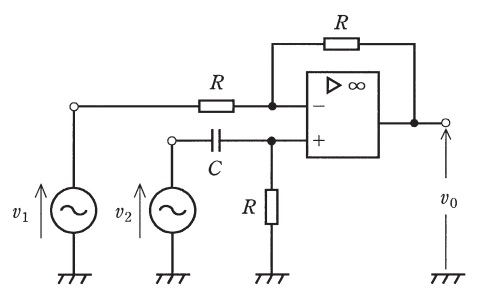
図の回路において，$\ v_{2}=0 \ $のとき，演算増幅器の出力電圧$\ v_{0}= \ \fbox {　 （１） 　} \ \times v_{1} \ $と表される。一方，$\ v_{1}=0 \ $のとき，演算増幅器の出力電圧$\ v_{0}= \ \fbox {　 （２） 　} \ \times v_{2} \ $と表される。さらに，これらのことから，$\ v_{1}=v_{2} \ $とすると，演算増幅器の出力電圧$\ v_{0}= \ \fbox {　 （３） 　} \ \times v_{1} \ $となることが分かる。$\ v_{1}=v_{2} \ $のとき，入力信号の角周波数$\ \omega \ $を零(直流)から無限大まで変化させて，電圧増幅度$\ \displaystyle \frac {v_{0}}{v_{1}} \ $の変化を調べると，電圧増幅度の絶対値は$\ \fbox {　 （４） 　} \ $である。また，電圧増幅度の$\ \omega =0 \ $における位相と$\ \omega \ $が無限大のときの位相との差は$\ \fbox {　 （５） 　} \ $度である。

〔問7の解答群〕
$$\begin{eqnarray} &（イ）&　\frac {2}{1+\mathrm {j}\omega CR}　　　　　&（ロ）&　90　　　　　&（ハ）&　-2 \\[ 5pt ] &（ニ）&　\frac {2\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}　　　　　&（ホ）&　\frac {1}{1+\mathrm {j}\omega CR}　　　　　&（ヘ）&　\frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR} \\[ 5pt ] &（ト）&　\frac {-1+\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}　　　　　&（チ）&　180 　　　　　&（リ）&　2 \\[ 5pt ] &（ヌ）&　360　　　　　&（ル）&　0.5　　　　　&（ヲ）&　1 \\[ 5pt ] &（ワ）&　0　　　　　&（カ）&　-1　　　　　&（ヨ）&　\frac {1-\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR} \end{eqnarray}$$

【ワンポイント解説】

オペアンプの基本を理解していれば，それほど計算は複雑ではありません。オペアンプの問題は比較的易しい問題が出題されることが多いので，演習を重ねて得意分野にしていきましょう。

1.理想的なオペアンプの特徴
１．電圧増幅率が無限大です。したがって，無限大でない有限数が出力される時，入力端子間の電圧は$\ 0 \ \mathrm {V} \ $(バーチャルショート)となります。
２．入力インピーダンスが無限大です。したがって入力端子に電流は流れません。
３．出力インピーダンスがゼロです。

【解答】

(1)解答：カ
$\ v_{2}=0 \ $の時，＋端子側の$\ C \ $と$\ R \ $には電流が流れないので，入力端子の＋端子の電圧は零であり，－端子の電圧も零である。
よって，問題図の$\ v_{1} \ $から抵抗$\ R \ $に流れる電流の大きさ$\ I_{1} \ $は，
$$I_{1}=\frac {v_{1}}{R}$$ となり，これがすべて演算増幅器の上側の抵抗に流れるので，出力電圧$\ v_{0} \ $は，
$$\begin{eqnarray} v_{0}&=&0-RI_{1} \\[ 5pt ] &=&-R\frac {v_{1}}{R} \\[ 5pt ] &=&-v_{1} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(2)解答：ニ
$\ R \ $と$\ C \ $の分圧の関係より，入力端子の＋端子の電圧$\ V_{+} \ $は，
$$\begin{eqnarray} V_{+}&=&\frac {R}{\displaystyle R+\frac {1}{\mathrm {j}\omega C}}v_{2} \\[ 5pt ] &=&\frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}v_{2} \\[ 5pt ] \end{eqnarray}$$ となる。よって，入力端子の－端子の電圧$\ V_{-} \ $も同値となる。$\ v_{1}=0 \ $であるので，抵抗$\ R \ $を通して－端子から$\ v_{1} \ $側へ流れる電流の大きさ$\ I_{2} \ $は，
$$\begin{eqnarray} I_{2}&=&\frac {V_{-}}{R} \\[ 5pt ] &=&\frac {\displaystyle \frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}v_{2}}{R} \\[ 5pt ] &=&\frac {\mathrm {j}\omega C}{1+\mathrm {j}\omega CR}v_{2} \\[ 5pt ] \end{eqnarray}$$ となる。したがって，出力電圧$\ v_{0} \ $は，
$$\begin{eqnarray} v_{0}&=&V_{-}+RI_{2} \\[ 5pt ] &=&\frac {\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}v_{2}+R\frac {\mathrm {j}\omega C}{1+\mathrm {j}\omega CR}v_{2} \\[ 5pt ] &=&\frac {2\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}v_{2} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(3)解答：ト
重ねの理より，$\ v_{1}=v_{2} \ $の時の出力電圧の大きさ$\ v_{0} \ $は，
$$\begin{eqnarray} v_{0}&=&-v_{1}+\frac {2\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}v_{2} \\[ 5pt ] &=&-v_{1}+\frac {2\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}v_{1} \\[ 5pt ] &=&\frac {-1+\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}v_{1} \\[ 5pt ] \end{eqnarray}$$ と求められる。

(4)解答：ヲ
電圧増幅度$\ \displaystyle \frac {v_{0}}{v_{1}} \ $の絶対値は，
$$\begin{eqnarray} \left| \frac {v_{0}}{v_{1}}\right| &=&\left| \frac {-1+\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}\right| \\[ 5pt ] &=&\frac {\sqrt {\left( -1\right) ^{2}+\left( \omega CR\right) ^{2}}}{\sqrt {1^{2}+\left( \omega CR\right) ^{2}}} \\[ 5pt ] &=&1 \\[ 5pt ] \end{eqnarray}$$ と求められる。

(5)解答：チ
$\ \omega =0 \ $の時と$\ \omega =\infty \ $の時の$\ \displaystyle \frac {v_{0}}{v_{1}} \ $の大きさは，
$$\begin{eqnarray} \displaystyle \lim_{ \omega \to 0 } \frac {v_{0}}{v_{1}} &=& \displaystyle \lim_{ \omega \to 0 } \left( \frac {-1+\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}\right) \\[ 5pt ] &=&-1 \\[ 5pt ] \displaystyle \lim_{ \omega \to \infty } \frac {v_{0}}{v_{1}} &=& \displaystyle \lim_{ \omega \to \infty } \left( \frac {-1+\mathrm {j}\omega CR}{1+\mathrm {j}\omega CR}\right) \\[ 5pt ] &=& \displaystyle \lim_{ \omega \to \infty } \left( \frac {\displaystyle -\frac {1}{\omega }+\mathrm {j} CR}{\displaystyle \frac {1}{\omega }+\mathrm {j}CR}\right) \\[ 5pt ] &=& \frac {\mathrm {j} CR}{\mathrm {j}CR} \\[ 5pt ] &=&1 \\[ 5pt ] \end{eqnarray}$$ となるので，$\ \omega =0 \ $の時と$\ \omega =\infty \ $の時の位相差は$\ 180° \ $となる。